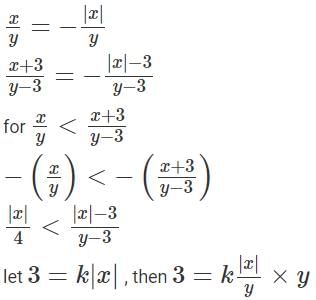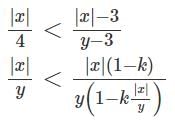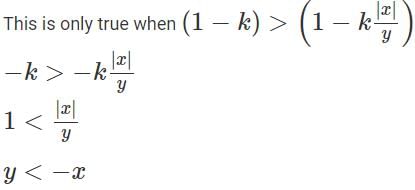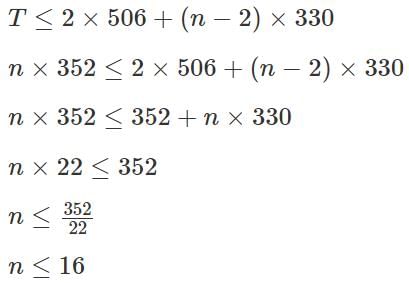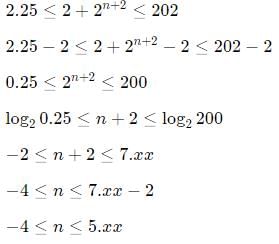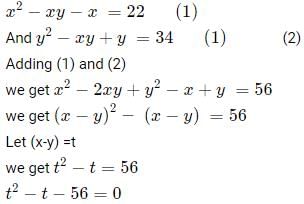CAT Exam > CAT Notes > Quantitative Aptitude (Quant) > CAT Previous Year Questions - Inequalities
Inequalities CAT Previous Year Questions with Answer PDF
Question for CAT Previous Year Questions - Inequalities
Try yourself:Any non-zero real numbers x, y such that y ≠ 3 and x/y <  will satisfy the condition
will satisfy the condition
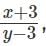 will satisfy the condition
will satisfy the condition
[2023]
View Solution
*Answer can only contain numeric values
Question for CAT Previous Year Questions - Inequalities
Try yourself:If a certain amount of money is divided equally among n persons, each one receives Rs 352. However, if two persons receive Rs 506 each and the remaining amount is divided equally among the other persons, each of them receive less than or equal to Rs 330. Then, the maximum possible value of n is
[2023]
Check
View Solution
Question for CAT Previous Year Questions - Inequalities
Try yourself:Let n and m be two positive integers such that there are exactly 41 integers greater than 8m and less than 8n (m<n), which can be expressed as powers of 2. Then, the smallest possible value of n + m is
[2023]
View Solution
*Answer can only contain numeric values
Question for CAT Previous Year Questions - Inequalities
Try yourself:For natural numbers x, y, and z, if xy + yz = 19 and yz + xz = 51, then the minimum possible value of xyz is
[2022]
Check
View Solution
Question for CAT Previous Year Questions - Inequalities
Try yourself:The number of integers n that satisfy the inequalities ∣n−60∣ < ∣n−100∣ <∣n−20∣ is
[2021]
View Solution
*Answer can only contain numeric values
Question for CAT Previous Year Questions - Inequalities
Try yourself:For all possible integers n satisfying 2.25 ≤ 2 + 2n+2 ≤ 202, then the number of integer values of 3 + 3n+1 is:
[2021]
Check
View Solution
Question for CAT Previous Year Questions - Inequalities
Try yourself:Consider the pair of equations: x2 − xy − x = 22 and y2 − xy + y = 34. If x > yx > y, then x - yx − y equals
[2021]
View Solution
*Answer can only contain numeric values
Question for CAT Previous Year Questions - Inequalities
Try yourself:The number of distinct pairs of integers (m,n), satisfying ∣1+mn∣ < ∣m+n∣ < 5 is:
[2021]
Check
View Solution
Question for CAT Previous Year Questions - Inequalities
Try yourself:The smallest integer n for which 4n > 1719 holds, is closest to
[2018]
View Solution
*Answer can only contain numeric values
Question for CAT Previous Year Questions - Inequalities
Try yourself:The smallest integer n such that n3 - 11n2 + 32n - 28 > 0 is
(TITA 2018)
Check
View Solution
*Answer can only contain numeric values
Question for CAT Previous Year Questions - Inequalities
Try yourself:If a and b are integers such that 2x2 − ax + 2 > 0 and x2 − bx + 8 ≥ 0 for all real numbers x, then the largest possible value of 2a − 6b is
(TITA 2018)
Check
View Solution
*Answer can only contain numeric values
Question for CAT Previous Year Questions - Inequalities
Try yourself:For how many integers n, will the inequality (n – 5) (n – 10) – 3(n – 2) ≤ 0 be satisfied?
(TITA 2017)
Check
View Solution
The document Inequalities CAT Previous Year Questions with Answer PDF is a part of the CAT Course Quantitative Aptitude (Quant).
All you need of CAT at this link: CAT
|
191 videos|133 docs|110 tests
|
FAQs on Inequalities CAT Previous Year Questions with Answer PDF
| 1. What are the types of inequalities commonly tested in the CAT exam? |  |
| 2. How can I solve inequalities algebraically during the CAT exam? |  |
Ans. To solve inequalities algebraically during the CAT exam, it is important to understand the properties of inequalities, such as adding or subtracting the same value on both sides, multiplying or dividing by a positive or negative number, and using the properties of absolute values.
| 3. Can graphical methods be used to solve inequalities in the CAT exam? |  |
Ans. Yes, graphical methods can be used to solve inequalities in the CAT exam. Plotting the inequalities on a number line or graphing the functions can help visualize the solution set and determine the range of values that satisfy the inequality.
| 4. How can I practice inequalities for the CAT exam? |  |
Ans. To practice inequalities for the CAT exam, it is recommended to solve a variety of inequality problems from previous year question papers, mock tests, and study materials. Additionally, practicing inequalities in a timed setting can help improve speed and accuracy.
| 5. Are inequalities an important topic for the CAT exam? |  |
Ans. Yes, inequalities are an important topic for the CAT exam as they frequently appear in the quantitative aptitude section. A strong understanding of inequalities and the ability to solve related problems can significantly impact your overall score in the exam.
Related Searches

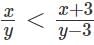 is always true, since We are increasing the numerator and decreasing the denominator.
is always true, since We are increasing the numerator and decreasing the denominator.
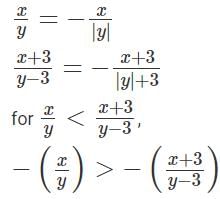
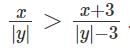 This is always true since we are increasing the numerator and decreasing the denominator.
This is always true since we are increasing the numerator and decreasing the denominator.