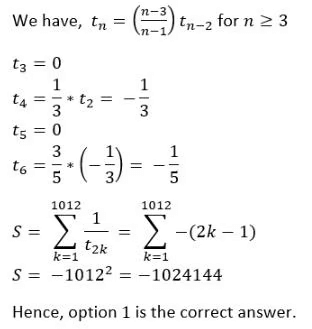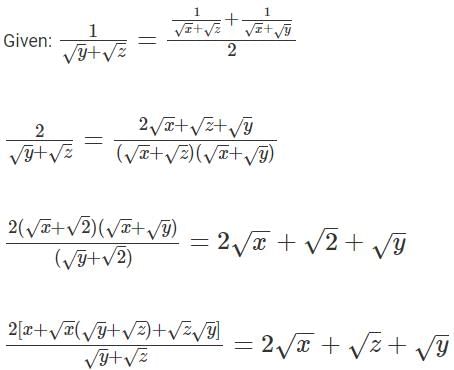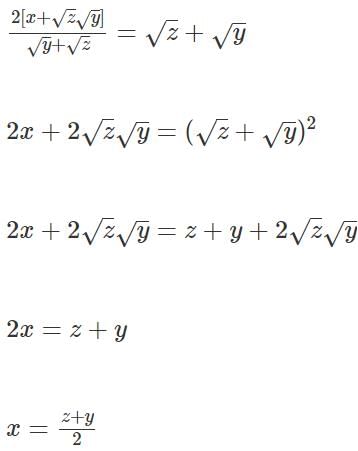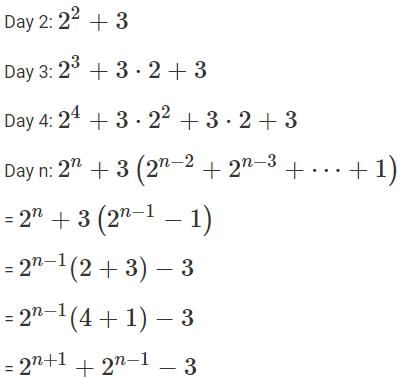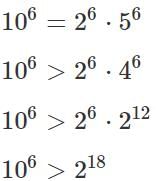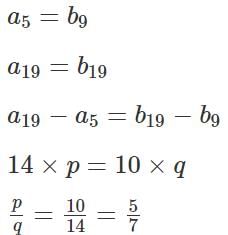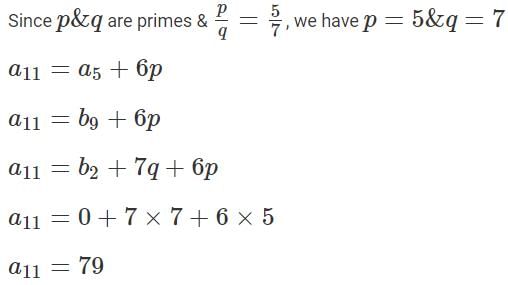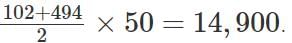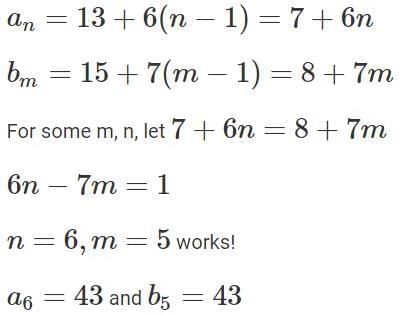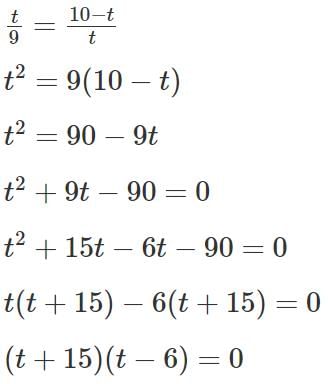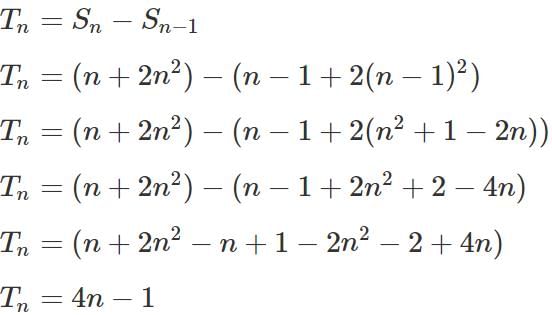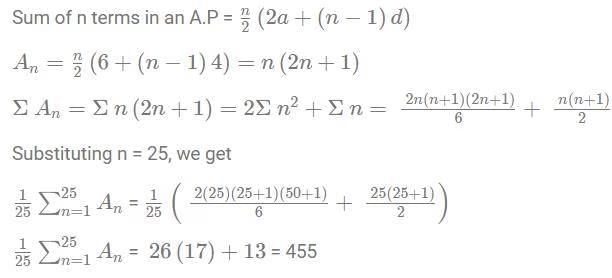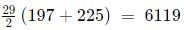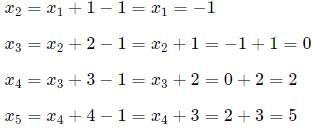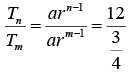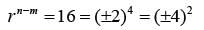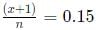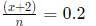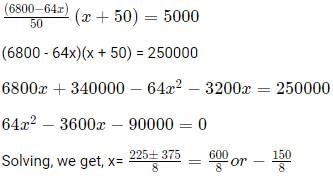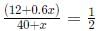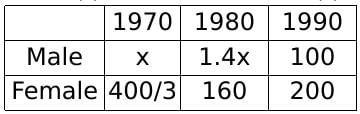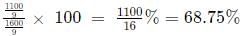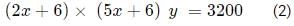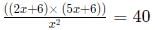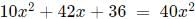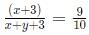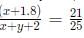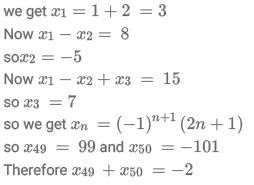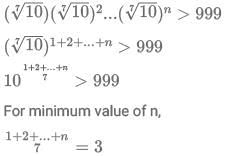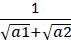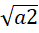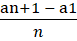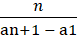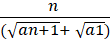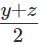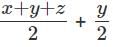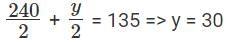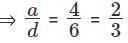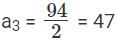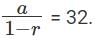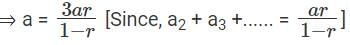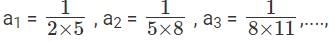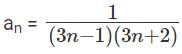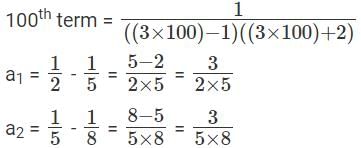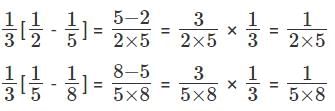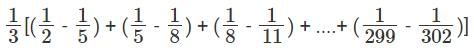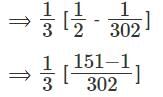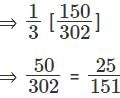Progressions CAT Previous Year Questions with Answer PDF
2024
Q1: The sum of the infinite series 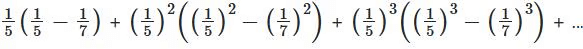 is equal to
is equal to
(a) 5/408
(b) 5/816
(c) 7/408
(d) 7/816
Ans: a
Sol:
Q2: Consider the sequence t1 = 1, t2 = -1 and tn = 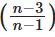 tn-2 for n ≥ 3. Then, the value of the sum
tn-2 for n ≥ 3. Then, the value of the sum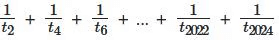
(a) -1024144
(b) -1022121
(c) -1026169
(d) -1023132
Ans: a
Sol:
2023
Q1: For some positive and distinct real numbers x, y and z, If 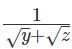 is the arithmetic mean of
is the arithmetic mean of 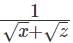 and
and 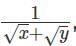 then the relationship which will always hold true, is [2023]
then the relationship which will always hold true, is [2023]
(a) √x, √y and √z are in arithmetic progression
(b) √x, √z and √y are in arithmetic progression
(c) y, x and z are in arithmetic progression
(d) x, y and z are in arithmetic progression
Ans: c
Sol:
x is the Arithmetic Mean of z & y, therefore, z, x, y form an A.P.
It goes without saying that y, x, z also forms an A.P.
Q2: A lab experiment measures the number of organisms at 8 am every day. Starting with 2 organisms on the first day, the number of organisms on any day is equal to 3 more than twice the number on the previous day. If the number of organisms on the nth day exceeds one million, then the lowest possible value of n is [2023]
Ans: 19
Sol: 1 Million = 106
Population on…
Day 1: 2
Putting n = 18 in 2n+1 + 2n−1−3 , we get 655357, which is less than 106
On the 19th day the population will be more than double the population on the 18th day, which is more than 2 × 655357, which is definitely more than 106.
Q3: A container has 40 liters of milk. Then, 4 liters are removed from the container and replaced with 4 liters of water. This process of replacing 4 liters of the liquid in the container with an equal volume of water is continued repeatedly. The smallest number of times of doing this process, after which the volume of milk in the container becomes less than that of water, is [2023]
Ans: 7
Sol: Every time 10% of the mixture is replace with a pure adulterant (here water), the concentration of the mixture becomes 90% of the initial concentration.
Similarly when a proportion p of a mixture is replaced with pure adulterant, the concentration of the mixture becomes (1 - p) times the previous concentration. (0 ≤ p ≤ 1)
Here p = 4/40 = 0.1
Initially there was pure milk, so the strength of the mixture is 100% or 1 (in terms of proportion)
After repeating the process n times the concentration of Milk in the mixture will be 1 × 0.9n
For the volume of milk to be less than the volume of water, p should be less than 0.5
So we are looking for the smallest n, such that 1 × 0.9n < 0.5
This happens when n = 7
Q4: Let both the series a1, a2, a3,… and b1, b2, b3… be in arithmetic progression such that the common differences of both the series are prime numbers. If a5 = b9, a19 = b19 and b2 = 0 , then a11 equals [2023]
(a) 79
(b) 83
(c) 86
(d) 84
Ans: a
Sol: Let the common differences of the series a1, a2, a3, … and b1, b2, b3 be p and q respectively.
We are told that p and q are prime numbers.
Q5: Let an = 46 + 8n and bn = 98 + 4n be two sequences for natural numbers n≤100 . Then, the sum of all terms common to both the sequences is [2023]
(a) 15000
(b) 14900
(c) 14602
(d) 14798
Ans: b
Sol: We have an = 46 + 8n and bm = 98 + 4m where n, m are positive integers ≤ 100.
Let's find the smallest possible values of m, n where an = bm
46 + 8n = 98 + 4m
8n - 4m = 52
2n - m = 13
n = 7, m = 1 are smallest values of m, n where an = bm.
a7 = b1 = 102
Therefore, the common elements in the series will be of the form 102+8k .
a100 = 846; b100 = 498
The largest natural number less than or equal to 498 and of the form 102 + 8k is 494.
So the common terms of both the series are
102 , 110, 118, ..., 494
102, 102 + 8, 102 + 8(2), ..., 102 + 8(49)
So, there are 50 terms in this A.P
Sum of all the terms =
Q6: The equation x3 + (2r + 1)x2 + (4r - 1)x + 2 = 0 has -2 as one of the roots. If the other two roots are real, then the minimum possible non-negative integer value of r is
Ans: 2
Sol:
Q7: The amount of job that Amal, Sunil and Kamal can individually do in a day, are in harmonic progression. Kamal takes twice as much time as Amal to do the same amount of job. If Amal and Sunil work for 4 days and 9 days, respectively, Kamal needs to work for 16 days to finish the remaining job. Then the number of days Sunil will take to finish the job working alone, is
Ans: 27
Sol: “The amount of job that Amal, Sunil and Kamal can individually do in a day, are in harmonic progression.” This implies that the amount of time taken individually by Amal, Sunil and Kamal to finish a job are in A.P.
“Kamal takes twice as much time as Amal to do the same amount of job.” Since the amount of time taken individually by Amal, Sunil and Kamal to finish a job are in A.P, this simply means that Sunil Should take 1.5 times the time as Amal to do the same amount of job.
So, to do the same amount of job individually, the times taken by Amal, Sunil and Kamal will be in the ratio, 1 : 1.5 : 2 or 2 : 3 : 4
Amal, Sunil and Kamal worked for 4, 9 and 16 days respectively to finish the job.
Sunil does in 3 days what Amal does in 2 days.
Therefore, Sunil does in 6 days what Amal does in 4 days.
Sunil does in 3 days what Kamal does in 4 days.
Therefore, Sunil does in 12 days what Kamal does in 16 days.
So, to finish the entire job on his own, Sunil would require, 6 + 9 + 12 = 27 days.
Q8: Let an and bn be two sequences such that an = 13 + 6(n − 1) and bn = 15 + 7(n − 1) foc. Then, the largest three digit integer that is common to both these sequences, is
Ans: 967
Sol:
2022
Q1: Trains A and B start traveling at the same time towards each other with constant speeds from stations X and Y, respectively. Train A reaches station Y in 10 minutes while train B takes 9 minutes to reach station X after meeting train A. Then the total time taken, in minutes, by train B to travel from station Y to station X is [2022]
(a) 15
(b) 12
(c) 6
(d) 10
Ans: a
Sol: Let the meeting point of the two trains between stations X and Y be M.
Let the time taken to reach M from X by train A be ‘t’ minutes. Since the two trains start simultaneously, the time taken by train B to reach M from Y will also be ‘t’ minutes.
We know that train A completes the entire journey in 10 minutes, so the time taken by train A to travel from M to Y will be ‘10 - t’ minutes. We are told that train B takes 9 minutes to reach X after it meets train A, which means, train B takes 9 minutes to travel from M to X.
When two bodies travel equal distances at constant speeds, the ratio of time taken by them to travel those distances will be the same.
The time taken by A and B to travel the distance between A and M is ‘t’ minutes and 9 minutes respectively. Similarly, the time taken by them to travel the distance between M and B is ‘10 - t’ and ‘t’ minutes.
The ratio of the times taken should be equal.
t = - 15 or t = 6
t can’t be negative, therefore, t is 6.
The total time taken by train B to reach station X from station Y is 6 + 9 =
15 minutes.
Q2: For any natural number n , suppose the sum of the first n terms of an arithmetic progression is (n + 2n2). If the nth term of the progression is divisible by 9, then the smallest possible value of n is [2022]
(a) 4
(b) 8
(c) 7
(d) 9
Ans: c
Sol: Let Sn stand for the sum of the first n terms of an arithmetic progression.
n, Sn = (n + 2n2)
Give Let Tn stand for the nth term of the same arithmetic progression.
The smallest value of n for which 4n - 1 is a multiple of 9 is 7.
n = 7
Q3: Consider the arithmetic progression 3, 7, 11, ... and let An denote the sum of the first n terms of this progression. Then the value of 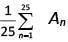 is
is
(a) 404
(b) 415
(c) 455
(d) 442
Ans: c
Sol:
Q4: On day one, there are 100 particles in a laboratory experiment. On day n, where n ≥ 2, one out of every n particles produces another particle. If the total number of particles in the laboratory experiment increases to 1000 on day m, then m equals
(a) 18
(b) 16
(c) 17
(d) 19
Ans: d
Sol:
Day 1 – 100 particles
Day 2 – 1 out of every 2 particles produces another particle. So, +50 particles
Day 3 – 1 out of every 3 particles produces another particle. So, +50 particles
We see that every day there is an increase of 50 particles.
1000 particles in (1000-100)/50 = 18 days after 1st day, i.e., in 19 days.
2021
Q1: The natural numbers are divided into groups as (1), (2, 3, 4), (5, 6, 7, 8, 9), ….. and so on. Then, the sum of the numbers in the 15th group is equal to [2021]
(a) 6119
(b) 6090
(c) 4941
(d) 7471
Ans: a
Sol: The first number in each group: 1, 2, 5, 10, 17.....
Their common difference is in Arithmetic Progression. Hence, the general term of the series can be expressed as a quadratic equation.
Let the quadratic equation of the general term be ax2 + bx + c
1st term = a + b + c = 1
2nd term = 4a + 2b + c = 2
3rd term = 9a + 3b + c = 5
Solving the equations, we get a = 1, b = -2, c = 2.
Hence, the first term in the 15th group will be (15)2 − 2(15) + 2 = 197
We can see that the number of terms in each group is 1, 3, 5, 7.... and so on. These are of the form 2n-1. Hence, the number of terms in 15th group will be 29. Hence, the last term in the 15th group will be 197 + 29 - 1 = 225.
Sum of terms in group 15
=
Q2: Three positive integers x, y and z are in arithmetic progression. If y - x > 2y − x > 2 and xyz = 5(x + y + z), then z-x equals
[2021]
(a) 8
(b) 12
(c) 14
(d) 10
Ans: c
Sol: Given x, y, z are three terms in an arithmetic progression.
Considering x = a, y = a + d, z = a + 2 x d.
Using the given equation x . y x z = 5 x (x + y + z)
a(a+d) x (a+2 x d) = 5(a + a + d + a + 2 x d)
= a(a + d) x (a + 2 x d) = 5(3 x a + 3 x d) = 15(a+d).
= a(a + 2 x d) = 15.
Since all x, y, z are positive integers and y - x > 2. a, a + d, a + 2d are integers.
The common difference is positive and greater than 2.
Among the different possibilities are : (a = 1, a + 2d = 5), (a, =3, a + 2d = 5), (a = 5, a + 2d = 3), (a = 15, a + 2d = 1)
Hence the only possible case satisfying the condition is :
a = 1, a + 2 x d = 15.
x = 1, z = 15.
z - x = 14.
Q3: Consider a sequence of real numbers, x1 ,x2 ,x3 ,... such that xn+1 = xn + n − 1 for all n ≥ 1. If x1 =−1 then x100 is equal to
[2021]
(a) 4849
(b) 4949
(c) 4950
(d) 4850
Ans: d
Sol: x1 = −1
......
If we observe the series, it is a series that has a difference between the consecutive terms in an AP.
Such series are represented as t(n) = a + bn + cn2
We need to find t(100).
t(1) = -1
a + b + c = -1
t(2) = -1
a + 2b + 4c = -1
t(3) = 0
a + 3b + 9c = 0
Solving we get,
b + 3c = 0
b + 5c = 1
c = 0.5
b = -1.5
a = 0
Now,
t(100) = (−1.5)100 + (0.5)1002 = −150 + 5000 = 4850
Q4: Let the m-th and n-th terms of a geometric progression be 3/4 and 12 , respectively, where m<n. If the common ratio of the progression is an integer r, then the smallest possible value of r + n - m is [2021]
(a) -2
(b) 2
(c) 6
(d) -4
Ans: a
Sol: Tn = 12
Tm = 3 / 4
To get the minimum value for r + n - m, r should be minimum.
∴ r = - 4
n - m = 2
∴ Required answer =-2
Q5: A box has 450 balls, each either white or black, there being as many metallic white balls as metallic black balls. If 40% of the white balls and 50% of the black balls are metallic, then the number of non-metallic balls in the box is [2021]
Ans: 250
Sol: Let the number of white balls be x and black balls be y
So we get x + y = 450 (1)
Now metallic black balls = 0.5y
Metallic white balls = 0.4x
From condition 0.4x= 0.5y
we get 4x - 5y = 0 (2)
Solving (1) and (2) we get
x = 250 and y = 200
Now number of Non Metallic balls = 0.6x + 0.5y = 150 + 100 = 250
Q6: In a football tournament, a player has played a certain number of matches and 10 more matches are to be played. If he scores a total of one goal over the next 10 matches, his overall average will be 0.15 goals per match. On the other hand, if he scores a total of two goals over the next 10 matches, his overall average will be 0.2 goals per match. The number of matches he has played is [2021]
Ans: 10
Sol: Let Total matches played be n and in initial n-10 matches his goals be x
so we get
we get x+1 =0.15n (1)
From condition (2) we get :
we get x + 2 = 0.2n (2)
Subtracting (1) and (2)
we get 1 = 0.05n
n = 20
So initially he played n - 10 =10 matches
Q7: A shop owner bought a total of 64 shirts from a wholesale market that came in two sizes, small and large. The price of a small shirt was INR 50 less than that of a large shirt. She paid a total of INR 5000 for the large shirts, and a total of INR 1800 for the small shirts. Then, the price of a large shirt and a small shirt together, in INR, is [2021]
(a) 175
(b) 150
(c) 200
(d) 225
Ans: c
Sol: Let the number of large shirts be l and the number of small shirts be s.
Let the price of a small shirt be x and that of a large shirt be x + 50.
Now, s + l = 64l (x + 50) = 5000
sx = 1800
Adding them, we get,
lx + sx + 50l = 6800
64x + 50l = 6800
Substituting l = (6800 - 64x) / 50, in the original equation, we get
So, x = 75
x + 50 = 125
Answer = 75 + 125 = 200.
Q8: In a tournament, a team has played 40 matches so far and won 30% of them. If they win 60% of the remaining matches, their overall win percentage will be 50%. Suppose they win 90% of the remaining matches, then the total number of matches won by the team in the tournament will be [2021]
(a) 80
(b) 78
(c) 84
(d) 86
Ans: c
Sol: Initially number of matches = 40
Now matches won = 12
Now let remaining matches be x
Now number of matches won = 0.6x
Now as per the condition :
24 +1.2x = 40 + x
0.2x = 16
x = 80
Now when they won 90% of remaining = 80(0.9) =72
So total won = 84
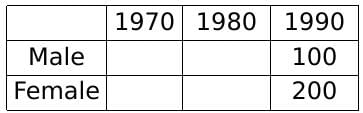
Q9: The total of male and female populations in a city increased by 25% from 1970 to 1980. During the same period, the male population increased by 40% while the female population increased by 20%. From 1980 to 1990, the female population increased by 25%. In 1990, if the female population is twice the male population, then the percentage increase in the total of male and female populations in the city from 1970 to 1990 is [2021]
(a) 68.25
(b) 68.75
(c) 68.50
(d) 69.25
Ans: b
Sol: Let us solve this question by assuming values(multiples of 100) and not variables(x).
Since we know that the female population was twice the male population in 1990, let us assume their respective values as 200 and 100.
Note that while assuming numbers, some of the population values might come out as a fraction(which is not possible, since the population needs to be a natural number). However, this would not affect our answer, since the calculations are in ratios and percentages and not real values of the population in any given year.
Now, we know that the female population became 1.25 times itself in 1990 from what it was in 1980.
Hence, the female population in 1980 = 200/1.25 = 160
Also, the female population became 1.2 times itself in 1980 from what it was in 1970.
Hence, the female population in 1970 = 160/1.2 = 1600/12 = 400/3
Let the male population in 1970 be x. Hence, the male population in 1980 is 1.4x.
Now, the total population in 1980 = 1.25 times the total population in 1970.
Hence, 1.25 (x + 400/3) = 1.4x + 160
Hence, x = 400/9.
Population change = 300 - 400/9 - 400/3 = 300 - 1600/9 = 1100/9
Percentage change
=
Q10: A tea shop offers tea in cups of three different sizes. The product of the prices, in INR, of three different sizes is equal to 800. The prices of the smallest size and the medium size are in the ratio 2 : 5. If the shop owner decides to increase the prices of the smallest and the medium ones by INR 6 keeping the price of the largest size unchanged, the product then changes to 3200. The sum of the original prices of three different sizes, in INR, is [2021]
Ans: 34
Sol: Let price of smallest cup be 2x and medium be 5x and large be y
Now by condition 1
2x × 5x × y =800
we get x2y =80 (1)
Now as per second condition ;
Now dividing (2) and (1)
we get
we get
we get 30x2 − 42x − 36=0
5x2 −7x − 6 = 0
we get x = 2
So 2x = 4 and 5x = 10
Now substituting in (1) we get y = 20
Now therefore sum = 4 + 10 + 20 = 34
Q11: If a certain weight of an alloy of silver and copper is mixed with 3 kg of pure silver, the resulting alloy will have 90% silver by weight. If the same weight of the initial alloy is mixed with 2 kg of another alloy which has 90% silver by weight, the resulting alloy will have 84% silver by weight. Then, the weight of the initial alloy, in kg, is [2021]
(a) 3.5
(b) 2.5
(c) 3
(d) 4
Ans: c
Sol: Let the alloy contain x Kg silver and y kg copper
Now when mixed with 3Kg Pure silver
we get
we get 10x + 30 = 9x + 9y + 27
9y - x = 3 (1)
Now as per condition 2
silver in 2nd alloy = 2(0.9) = 1.8
So we get
we get 21y -4x =3 (2)
solving (1) and (2) we get y= 0.6 and x = 2.4
so x + y = 3
Q12: For a sequence of real numbers 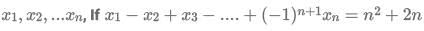 for all natural numbers n, then the sum
for all natural numbers n, then the sum 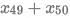 equals
equals
(a) 200
(b) 2
(c) -260
(d) -2
Ans: d
Sol: Now as per the given series :
Q13: If n is a positive integer such that 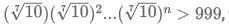 then the smallest value of n is
then the smallest value of n is
Ans: 6
Sol:1 + 2 + ... + n = 21
We can see that if n = 6, 1 + 2 + 3 + ... + 6 = 21.
2019
Q1: If the population of a town is p in the beginning of any year then it becomes 3+2p in the beginning of the next year. If the population in the beginning of 2019 is 1000, then the population in the beginning of 2034 will be [2019]
(a) (1003)15 + 6
(b) (977)15 - 3
(c) (1003)215 - 3
(d) (977)214 + 3
Ans: c
Sol: From the given data,
Simplifying,
P increases in the series of 20P ,21P, 22P, 23P,... and so on
2034 is 15 years after 2019. So, the first part of the value would be 215 p
Now, let us observe the second pattern.
In 2021, the value increases to 2(2p + 3) + 3
On expanding, (2 x 2) +(2 x 3) + 3 = 2 x 2 + 3(1 + 2)
In 2022, the value increases to 2[2(2p+3) +3]+3
On expanding, 2((2 x 2p) + (2 x 3) + 3) + 3
= (2 x 2 x 2 x p) + (2x 2 x 3) + (2 x 3) + 3
= (2 x 2 x 2 x p) + 3(20 + 21 + 22)
In 2034, the value of the second part would be 3 (20 + 21 + 22 +.... +214 )
On simplifying using Geometric progression we get, 3 () = 3 (215 - 1)
Total population = 215p +3 (215 - 1)
Substituting p = 1000,
Total population = (215 x 1003) - 3
Q2: If a1 + a2 + a3 + ... + an = 3(2n+1 - 2), then a11 equals [TITA 2019]
Ans: 6144
Sol: Let n = 1,
a1 = 3(21+1 -2) = 3(4-2) = 6 = 3 x 21
a2 = 3(22+1 -2) = 3(8-2) = 18, a2 = 18 - 6 = 12 = 3 x 22
a3 = 3(23+1 -2) = 3(14) = 42 a3 = 42 - 12 - 6 = 42-18 =24 = 3 x 23
So, a11 = 3 x 211 = 3 x 2048
a11 = 6144
Q3: If a1, a2, ......... are in A.P, 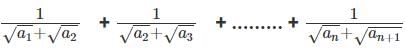 then , is equal to [2019]
then , is equal to [2019]
(a) 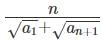
(b) 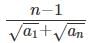
(c) 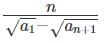
(d) 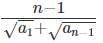
Ans: a
Sol: Consider the first term
Multiply numerator and denominator by-
We get. We know, a2 - a1 = d
Similarly, repeat the same for the entire series.
We get+ ..... +
=
(
-
)
We do not know the value of d.
We know an+1 = a1 + nd
an+1 - a1 = nd
d ==
So, our expression ==
2018
Q1: The arithmetic mean of x, y and z is 80, and that of x, y, z, u and v is 75, where u = 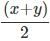 and v =
and v = 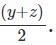 If x ≥ z, then the minimum possible value of x is (TITA 2018)
If x ≥ z, then the minimum possible value of x is (TITA 2018)
Ans: 105
Sol: Given that AM (x, y, z) = 80
So, x + y + z = 80 × 3 = 240 ...(1)
Also, AM (x, y, z, u, v) = 75
So, x + y + z + u + v = 75 × 5 = 375 ...(2)
Equation (2) – (1), we get
u + v = 375 - 240 = 135
Its also given that, u =and v =
So, u + v =
Substituting this value in (1), we get x + z = 210
It’s given that x ≥ z
x would take the minimum value when x = z
⇒ 2x = 210
⇒ x (min) = 105
2017
Q1: If the square of the 7th term of an arithmetic progression with positive common difference equals the product of the 3rd and 17th terms, then the ratio of the first term to the common difference is: [2017]
(a) 2 : 3
(b) 3 : 2
(c) 3 : 4
(d) 4 : 3
Ans: a
Sol: Given that the square of the 7th term of an arithmetic progression with positive common difference equals the product of the 3rd and 17th terms
(a + 6d)2 = (a + 2d)(a + 16d)
We have to find the ratio of the first term to the common difference
⇒ (a + 6d)2 = (a + 2d)(a + 16d)
⇒ a2 + 12d + 36 = a2 + 2ad + 16ad + 32d2
⇒ 4d2 + 12 ad – 18 ad = 0
⇒ 4d2 = 6ad
⇒ 4d = 6a
The ratio of first term to the common difference is 2 : 3.
Q2: Let a1, a2,.......a3n be an arithmetic progression with a1 = 3 and a2 = 7. If a1 + a2 + ......+a3n = 1830, then what is the smallest positive integer m such that m (a1 + a2 + ..... + an) > 1830? [2017]
(a) 8
(b) 9
(c) 10
(d) 11
Ans: b
Sol: Let us assume 3n = k
⇒ k/2 (2a + (k – 1)d) = 1830 we know that a = 3, d = 4
⇒ k/2 (2(3) + (k – 1)4) = 1830
⇒ k/2 (6 + 4k – 4) = 1830
⇒ k (2k + 1) = 1830
⇒ 2k2 + k = 1830
⇒ 2k2 + k – 1830 = 0
By factorizing we can find that k = 30, n = 10
⇒ 10/2 (2(3) + 4(9)) = 5(6 + 36)
⇒ 5(42) = 210
⇒ m (a1 + a2 + ..... + an) > 1830
⇒ 210 × m > 1830
⇒ m = 9, since 210 × 9 = 1890
Q3: Let a1, a2, a3, a4, a5 be a sequence of five consecutive odd numbers. Consider a new sequence of five consecutive even numbers ending with 2a3. If the sum of the numbers in the new sequence is 450, then a5 is [TITA 2017]
Ans: 51
Sol: Let a1, a2, a3, a4, a5 be n - 4 , n - 2 , n , n + 2 ,n + 4 respectively which is the sequence of consecutive odd numbers, where n = a3.
Let the new sequence of five consecutive even numbers be m - 4, m - 2, m, m + 2, m + 4.
Where the last term m + 4 = 2a3 = 450
Average of any number of terms in AP is the middle term
5 terms in AP ⇒ 5 × (middle term) = 450
⇒ Middle term (m) = 90
⇒ m - 4, m - 2, m, m + 2, m + 4 is equal to 86, 88, 90, 92, and 94 respectively.
⇒ 2a3 = 94
⇒
Hence a1, a2, a3, a4, a5 is equal to 43, 45, 47, 49, and 51 respectively.
Therefore a5 = 51
Q4: An infinite geometric progression a1, a2, a3,... has the property that an = 3(an+1 + an+2 +....) for every n ≥ 1. If the sum a1 + a2 + a3 +...... = 32, then a5 is [2017]
(a) 1/32
(b) 2/32
(c) 3/32
(d) 4/32
Ans: c
Sol: The sum up to infinity, a1 + a2 + a3 +...... = 32.
It can also be written as
We have been given that, an = 3(an+1 + an+2 +....) if n ≥ 1.
When n = 1, we get,
a = 3(a2 + a3 + .....)
⇒ 1 – r = 3r
⇒ 1 = 4r
⇒ r = 1/4
Now finding the value of a is easy.
a = 32 × (1 - (1/4))
⇒ a = 32 × (3/4)
⇒ a = 24
The value of a5 = ar4 , where a = 24 and r4 = (1/4)4
Q5: If 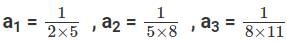 ,..., then a1 + a2 + a3 + ...... + a100 is [2017]
,..., then a1 + a2 + a3 + ...... + a100 is [2017]
(a) 25/151
(b) 1/2
(c) 1/4
(d) 111/55
Ans: a
Sol: Given that
We have to find a1 + a2 + a3 + ...... + a100
This can be done by partial fractions
a1 = 3 - 1 = 2 , a2 = 6 - 1 = 5 , a3 = 9 – 1 = 8.
But these are not of the formHence these are written as,
Hence this can be written as,
|
184 videos|212 docs|103 tests
|
FAQs on Progressions CAT Previous Year Questions with Answer PDF
| 1. What are the different types of progressions commonly found in mathematics? |  |
| 2. How do you find the nth term of an arithmetic progression? |  |
| 3. What is the sum of the first n terms of an arithmetic progression? |  |
| 4. How do you determine if a sequence is a geometric progression? |  |
| 5. What is the sum of an infinite geometric progression? |  |