Detailed Notes Proportion - & Pedagogy Paper 2 for CTET & TET Exams - CTET & State

Introduction

• When two ratios are equal, the four quantities composing them are said to be proportional.
• Thus, if a/b = c/d, then a, b, c, d are proportional; this is expressed by saying that a is to b as c is to d, written as a:b::c:d or a:b = c:d.

• The terms a and d are called the extremes while the terms b and c are called the means.

Product of Extremes = Product of Means

Example: What is the value of x in the following expression?
5/8 = x/12

Solution:
5/8 = x/12
5 × 12 = 8 × x
x = 60/8
x = 7.5
An alternate reasoning using percentage: the denominator increases from 8 to 12 (an increase of 50%), so the numerator 5 increases by 50% giving 7.5.

Operations in Proportions

If four quantities a, b, c, d form a proportion, several equivalent proportions may be deduced by properties of fractions. The following operations are commonly used:

• Invertendo: If a/b = c/d then b/a = d/c.
• Alternando: If a/b = c/d then a/c = b/d.
• Componendo: If a/b = c/d then (a + b)/b = (c + d)/d.
• Dividendo: If a/b = c/d then (a − b)/b = (c − d)/d.

Componendo and Dividendo combined: If a/b = c/d then (a + b)/(a − b) = (c + d)/(c − d).

Variation

Two quantities A and B are said to vary with each other if a change in one is accompanied by a predictable change in the other according to a fixed rule.

Some typical examples of variation

• The area of a circle, A = πR², varies as the square of its radius R.
• At constant temperature, pressure is inversely proportional to volume (Boyle's law): P ∝ 1/V.
• If the speed of a vehicle is constant, the distance covered is directly proportional to time: D ∝ t.

Essentially there are two kinds of proportion relating two variables:

Direct Proportion

When A varies directly as B, we write A ∝ B, which means A = kB for some constant k (called the constant of proportionality).

• Logical implication: When A increases, B increases.
• Calculation implication: If A increases by 10%, B also increases by 10%.
• Graphical implication: The graph of A versus B is a straight line through the origin.

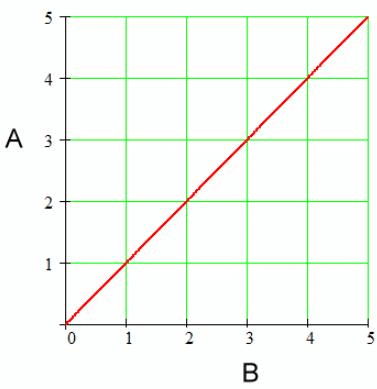
Inverse Proportion

When A varies inversely as B, we write A ∝ 1/B, which means A = k/B for some constant k.

• Logical implication: When A increases, B decreases.
• Calculation implication: Small percentage decreases in A correspond approximately to equivalent percentage increases in B when changes are small (reciprocal relationship).
• Graphical implication: The graph of A versus B is a rectangular hyperbola.
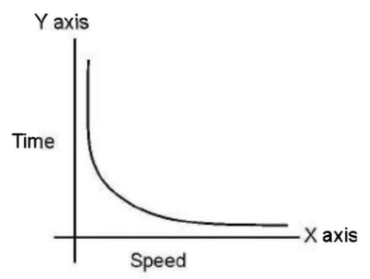
• Equation implication: The product A × B is constant.

Example 1: The height of a tree varies as the square root of its age (between 5 and 17 years). When the age is 9 years, the height is 4 feet. What is the height at age 16?

Solution:
Assume height H and age A.
H ∝ √A
H = K × √A
4 = K × √9
K = 4/3
Height at age 16: H = K × √16
H = (4/3) × 4
H = 16/3 feet
16/3 feet = 5 feet 4 inches

Note: Problems often involve ratios and proportions among several variables. If three quantities are in the ratio 4 : 6 : 9, it is standard to represent them as 4x, 6x, 9x for some common multiplier x. If a total or other relation is given, add the expressions to form a linear equation in x and solve for x.

For example, if the sum of three numbers in the ratio 4 : 6 : 9 is S, then 4x + 6x + 9x = 19x = S, so x = S/19 and the numbers are 4(S/19), 6(S/19), 9(S/19).

Methods and Important Types of Proportion Problems

This section outlines standard methods and additional proportion types commonly tested.

Cross-multiplication (basic solving technique)

• Given a/b = c/d, cross-multiplying gives ad = bc.
• Cross-multiplication is the usual first step in finding an unknown term in a proportion.

Unitary method

• Find the value of one unit by dividing, then multiply to get the desired quantity.
• This method is particularly useful when converting ratios to actual values given a total or another relation.

Compound proportion

• Compound proportion involves more than two variables where the combined effect is obtained by treating proportions stepwise or by multiplying factors of change.
• Example: If wages vary directly with number of workers and time, and inversely with work per person, combine the proportional factors multiplicatively to get net effect.

Continued proportion

• Three numbers a, b, c are in continued proportion if a : b = b : c, which implies b² = ac.
• Useful in geometric mean calculations and sequence problems.

Solving ratio problems - a checklist

• Express all given ratios in simplest terms.
• Introduce a common multiplier (like x) for each ratio part when converting ratios into actual quantities.
• Use cross-multiplication for simple proportions; use algebraic equations when totals or differences are given.
• Check units and ensure consistency (time, speed, distance, area, etc.).
• Verify answers by substituting back into original proportion relations.

Worked Example: Interpreting a Ratio Problem

Example: Three quantities are in the ratio 4 : 6 : 9 and their sum is 190. Find each quantity.

Solution:
Represent the quantities as 4x, 6x and 9x.
Sum = 4x + 6x + 9x
Sum = 19x
19x = 190
x = 10
Quantities are 4x = 40, 6x = 60, 9x = 90.

Summary and Examination Tips

• Remember the terminology: means and extremes and the relation ad = bc for a/b = c/d.
• Use cross-multiplication to solve for unknowns in simple proportions.
• Identify whether the relation is direct, inverse, square, or any other power law and set up equations accordingly (for example, A ∝ B^n).
• For multi-part ratio problems, introduce a common multiplier for each ratio part and translate given totals or conditions into linear equations.
• Familiarise yourself with operations on proportions (invertendo, alternando, componendo, dividendo) to transform equations quickly during problem solving.