Ratio and Proportions is one of the easiest concepts in CAT. It is just an extension of high school mathematics.
- Questions from this concept are mostly asked in conjunction with other concepts like similar triangles, mixtures and alligations.
- Hence fundamentals of this concept are important not just from a stand-alone perspective, but also to answer questions from other concept
1. Ratio is the comparison between similar types of quantities; it is an abstract quantity and does not have any units.
2. If a/b = c/d , then a, b, c, d are said to be in proportion.
3. If a/b = c/d, then
- If a, b, x are positive, then
- If a > b, then a + x/b + x < a/b
- Ifa<b,then a + x/b + x > a/b
- Ifa>b,then a − x/b − x > a/b
- If a<b,then a − x/b -x <a/b
4. Ifa/p = b/q = c/r = d/s =...,then a : b : c : d:... = p : q : r : s:...
(a) a × d = c × b
5. If a, b, x are positive, then
- If a>b, then a+x/b+x <a/b
- Ifa<b,then a+x/b+x >a/b
- Ifa>b,then a−x/b−x >a/b
- If a<b,then a−x/b-x<a/b
6. If a/p = b/q = c/r = d/s =...,then a : b : c : d:...= p : q : r : s:...
7. 
8. Types of ratios:
- Duplicate Ratio of a:b is a2 : b2
- Sub-duplicate ratio of a:b is Sqrt(a): Sqrt(b)
- Triplicate Ratio of a : b is a3 : b3
- Sub-triplicate ratio of a : b is a1/3 : b1/3
Product of proportions
1. If a:b = c : d is a proportion, then
- Product of extremes = product of means i.e., ad = bc
- Denominator addition/subtraction: a:a+b = c : c + d and a : a - b = c : c - d
- a, b, c, d,.... are in continued proportion means, a : b = b : c = c : d = ....
- a : b = b : c then b is called mean proportional and b2 = ac
- The third proportional of two numbers, a and b, is c, such that, a : b = b : c
- d is fourth proportional to numbers a, b, c if a : b = c : d
Variations:
1. If a ∝ b, provided c is constant and a ∞ c, provided b is constant, then a ∝ b x c if all three of them are varying.
2. If A and B are in a business for the same time, then Profit distribution ∝ investment (Time is constant).
3. If A and B are in a business with the same investment, then Profit distribution of investment ∝ Time (Investment is constant).
4. Profit Distribution ∝ investment
EduRev's Tip: If a/b = c/d = e/f = k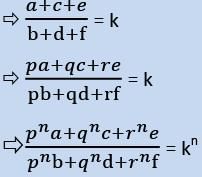
Given two variables x and y, y is (directly) proportional to x (x and y vary directly, or x and y are in direct variation) if there is a non-zero constant k such that y = kx. It is denoted by y ∝ x Two variables are inversely proportional (or varying inversely, or in inverse variation, or in inverse proportion or reciprocal proportion) if there exists a nonzero constant k such that y = k/x.
FAQs on Ratio, Proportion & Variation Formula - CAT
| 1. What is the formula for calculating the ratio between two quantities? |  |
| 2. How can the concept of proportion be applied in real-life situations? |  |
| 3. What is the formula for direct variation in mathematics? |  |
| 4. Can you provide an example of an inverse variation problem and its solution? |  |
| 5. How is the concept of variation useful in solving problems involving proportions? |  |














