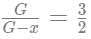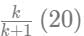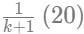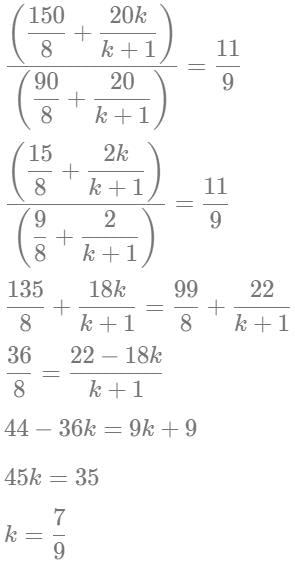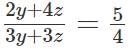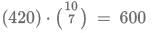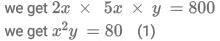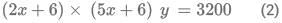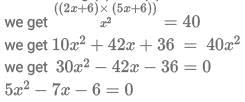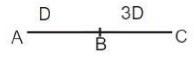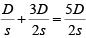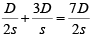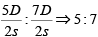CAT Previous Year Questions: Ratio & Proportion

Table of Contents
1. 2025
2. 2024
3. 2023
4. 2022
5. 2021
6. 2020
7. 2019
8. 2018
9. 2017
View more

From 2017 to 2025, ratio and proportion questions consistently appeared in CAT Quant, typically 2-7 questions per year. They commonly involved mixtures, ages, profit-loss, income distribution, percentages, and combined ratio concepts. Most were moderate in difficulty, often requiring structured multi-step reasoning and careful proportional analysis.

Ans: d
Sol: Let M = 13k, A = 9k. 
After 21 students were moved So
So, the number of students in the morning and afternoon shifts are 819 - 21 = 798, 567 + 21 = 588 respectively.
 Let's assume that 3t and 8t students joined the respective sessions.
 
Number of new students = 11t = 99

Q2: The ratio of expenditures of Lakshmi and Meenakshi is 2 : 3, and the ratio of income of Lakshmi to expenditure of Meenakshi is 6 : 7. If excess of income over expenditure is saved by Lakshmi and Meenakshi, and the ratio of their savings is 4 : 9, then the ratio of their incomes is
(a) 3:5 
(b) 5:6 
(c) 2:1 
(d) 7:8

Ans: a
Sol: Let Lakshmi's income = A and expenditure = B.
Let Meenakshi's income = C and expenditure = D.
From B:D = 2:3, take B = 2k and D = 3k.

Let Meenakshi's saving = C - D = C - 3k = C - D = C - 3k. 
Given the savings ratio

Q3: A certain amount of money was divided among Pinu, Meena, Rinu and Seema. Pinu received 20% of the total amount and Meena received 40% of the remaining amount. If Seema received 20% less than Pinu, the ratio of the amounts received by Pinu and Rinu is
(a) 2:1 
(b) 1:2 
(c) 5:8 
(d) 8:5

Ans: c
Sol: Let the total amount be 100 units (taking 100 makes percentage calculations easy).
Pinu receives 20% of the total, so Pinu gets 20 units.
The amount left after giving Pinu his share is 100 - 20 = 80 units.

Meena receives 40% of this remaining amount, so Meena gets 40% of 80 = 32 units.
Now, the amount left for Rinu and Seema together is 80 - 32 = 48 units.

Seema receives 20% less than Pinu. Since Pinu gets 20 units, Seema gets
20 - 20% of 20 = 20 - 4 = 16 units.

Out of the 48 units left for Rinu and Seema, Seema's share is 16 units, so Rinu gets
48 - 16 = 32 units.

Therefore, Pinu receives 20 units, and Rinu gets 32 units.
The required ratio of the amounts received by Pinu : Rinu = 20 : 32 = 5 : 8.

Q4: The ratio of the number of coins in boxes A and B was 17:7. After 108 coins were shifted from box A to box B, this ratio became 37:20. The number of coins that needs to be shifted further from A to B, to make this ratio 1:1, is

Ans: 272

Sol: Let the initial total number of coins in box A be 17x, since the ratio of the number of coins in boxes A and B is 17:7, the initial total number of coins in box B would be 7x.

After 108 coins are shifted from box A to box B, the number of coins in box A would be 17x - 108 and in box B would be 7x+108. We have,

Therefore, the total number of coins in the two boxes combined are (17 + 7)∗76 = 1824, half of which is 912. The number of coins in box B currently is 7 ∗ 76 + 108 = 640. The number of coins needed to make the coins equal in both the boxes is, 912 - 640 = 272.

Thus, 272 coins will be transferred from box A to box B to make the number of coins equal (1:1) in both the boxes.

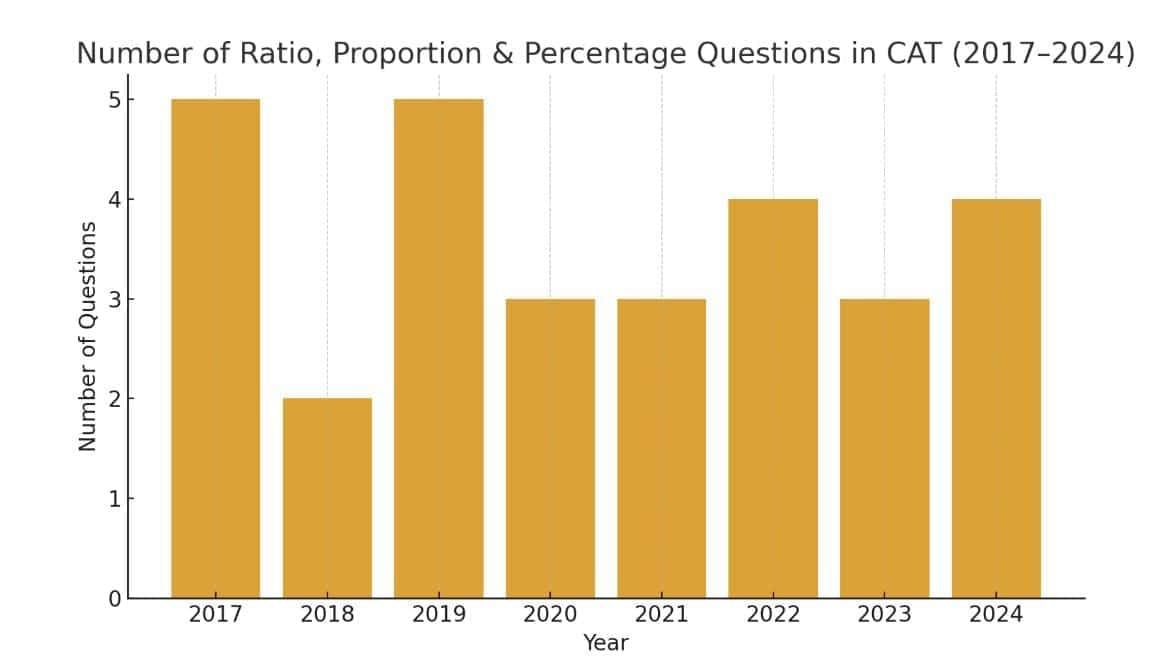
2024

Q1: In September, the incomes of Kamal, Amal and Vimal are in the ratio 8 ∶ 6 ∶ 5. They rent a house together, and Kamal pays 15%, Amal pays 12% and Vimal pays 18% of their respective incomes to cover the total house rent in that month. In October, the house rent remains unchanged while their incomes increase by 10%, 12% and 15%, respectively. In October, the percentage of their total income that will be paid as house rent, is nearest to 
(a) 12.75
(b) 14.84
(c) 15.18
(d) 13.26

Ans: d

Sol: 

Q2: A fruit seller has a total of 187 fruits consisting of apples, mangoes and oranges. The number of apples and mangoes are in the ratio 5 : 2. After she sells 75 apples, 26 mangoes and half of the oranges, the ratio of number of unsold apples to number of unsold oranges becomes 3 : 2. The total number of unsold fruits is 

Ans: 66

Sol: 

Q3: A vessel contained a certain amount of a solution of acid and water. When 2 litres of water was added to it, the new solution had 50% acid concentration. When 15 litres of acid was further added to this new solution, the final solution had 80% acid concentration. The ratio of water and acid in the original solution was 
(a) 4 : 5
(b) 5 : 3
(c) 5 : 4
(d) 3 : 5

Ans: (d)
Sol: At the time when, concentration was 50%
 Let x is acid and x is water.
 When 15 litres of acid is added then, the acid concentration becomes 80%
On solving, we get x = 5So, there were 5 litres of acid and 5 litres of water after mixing 2 litres of water:
So, there would be 5 litres of acid and 3 litres of water before adding the water.
So, the required ratio of acid to water would be 3 : 5
Hence, option D is the required answer.

Q4: When Rajesh's age was same as the present age of Garima, the ratio of their ages was 3 : 2. When Garima's age becomes the same as the present age of Rajesh, the ratio of the ages of Rajesh and Garima will become 
(a) 5 : 4
(b) 4 : 3
(c) 2 : 1
(d) 3 : 2

Ans: (a)
Sol: Assume the present age of Rajesh and Garima be x and y respectively.
Let's x - y = n [Rajesh is older than Garima]
When, Rajesh was of the age of Garima, which was n years ago, Garima was of (y - n) years old.
According to the given ratio,
y/(y-n) = 3 / 2
y = 3n
So, x = 4n
Now, when Garima become 4n years old, by that time, Rajesh will be 5n years old.
Hence, the required ratio = 5 : 4

Q5: A fruit seller has a total of 187 fruits consisting of apples, mangoes and oranges. The number of apples and mangoes are in the ratio 5 : 2. After she sells 75 apples, 26 mangoes and half of the oranges, the ratio of number of unsold apples to number of unsold oranges becomes 3 : 2. The total number of unsold fruits is  [2024]

 Ans: 66

Sol: The number of apples and mangoes are in the ratio 5 : 2.
 Let us write the number of apples as 5X and number of mangoes as 2X
 This means oranges will be 187-7X. 
 After selling the remaining fruits, 
 Apples: 5X-75
 Mangoes: 2X-26
 Oranges: (187-7X)/2
 Unsold Apples to Unsold oranges is 3:2

 20x-300=561-21x
 41x=861
 x=21
 Total number of unsold fruits will be, 
 Apples: 30
 Mangoes: 16
 Oranges: 20
 Total is 66. 

Q6: When Rajesh's age was same as the present age of Garima, the ratio of their ages was 3 : 2. When Garima's age becomes the same as the present age of Rajesh, the ratio of the ages of Rajesh and Garima will become  [2024]
(a) 5 : 4
(b) 4 : 3
(c) 2 : 1
(d) 3 : 2

Ans: a

Sol: Let's take Rajesh and Garima's ages to be R and G, respectively
 From the given ratio, we can see that Rajesh is older than Garima, so let's take R=G+x
 When Rajesh was of age G, which was x years ago, Garima was of G-x years old
Giving the ratio as
 This gives us G as 3x, which in turn gives R as 4x
 We are asked the ratio when Gramia becomes 4x years old. 
 By that time, Rajesh will be 5x years old. 
Giinv their ratio as
 Therefore, Option A is the correct answer. 

Q7: Rajesh and Vimal own 20 hectares and 30 hectares of agricultural land, respectively, which are entirely covered by wheat and mustard crops. The cultivation area of wheat and mustard in the land owned by Vimal are in the ratio of 5 : 3. If the total cultivation area of wheat and mustard are in the ratio 11 : 9, then the ratio of cultivation area of wheat and mustard in the land owned by Rajesh is [2024]
(a) 4 : 3
(b) 7 : 9
(c) 3 : 7
(d) 1 : 1

Ans: b

Sol: We are told that Rajesh manages 20 hectares and Vimal manages 30 hectares
 For Vimal, we know the distribution of the land between Wheat and Mustard, 5:3
 So, wheat area will be, 5/8 (30)
 Mustard area will be, 3/8 (30)
 Similarly, let us assume that the distribution of crops between Wheat and Mustard to be k:1
Wheat will be,
Mustard will be,
 We are told that total area of Wheat and Mustard is in the ratio 11:9
 Adding them up we get, 

 Hence the ratio of distribution of area between Wheat and Mustard for Rajesh is 7/9

2023

Q1: In a company, 20% of the employees work in the manufacturing department. If the total salary obtained by all the manufacturing employees is one-sixth of the total salary obtained by all the employees in the company, then the ratio of the average salary obtained by the manufacturing employees to the average salary obtained by the non-manufacturing employees is  [2023]
(a) 4 : 5
(b) 5 : 6
(c) 5 : 4
(d) 6 : 5

Ans: a

Sol: Let the number of total employees in the company be 100x, and the total salary of all the employees be 100y.

It is given that 20% of the employees work in the manufacturing department, and the total salary obtained by all the manufacturing employees is one-sixth of the total salary obtained by all the employees in the company.

Hence, the total number of employees in the manufacturing department is 20x, and the total salary received by them is (100y/6)

Average salary in the manufacturing department = (100y/6*20x) = 5y/6x

Similarly, the total number of employees in the nonmanufacturing department is 80x, and the total salary received by them is (500y/6)

Hence, the average salary in the nonmanufacturing department = (500y/6*80x) = 25y/24x

Hence, the ratio is:- (5y/6x): (25y/24x) 

⇒ 120: 150 = 4:5

Q2: Anil mixes cocoa with sugar in the ratio 3 : 2 to prepare mixture A, and coffee with sugar in the ratio 7 : 3 to prepare mixture B. He combines mixtures A and B in the ratio 2 : 3 to make a new mixture C. If he mixes C with an equal amount of milk to make a drink, then the percentage of sugar in this drink will be  [2023]
(a) 17
(b) 16
(c) 21
(d) 24

Ans: a

Sol: Let the volume of mixture A be 200 ml, which implies the quantity of cocoa in the mixture is 120 ml, and the quantity of sugar In the mixture 80 ml.

Similarly, let the volume of the mixture be 300 ml, which implies the quantity of coffee, and sugar in the mixture is 210, and 90 ml, respectively.

Now we combine mixture A, and B in the ratio of 2:3 (if 200 ml mixture A, then 300 ml of mixture B).

Hence, the volume of the mixture C is (200+300) = 500 ml, and the quantity of the sugar is (90+80) = 170 ml. 

Now he mixes C with an equal amount of milk to make a drink, which implies the quantity of the final mixture is (500+500) = 1000 ml.

The quantity of sugar in the final mixture is 170 ml.

Hence, the percentage is 17% 

Q3: The number of coins collected per week by two coin-collectors A and B are in the ratio 3 : 4. If the total number of coins collected by A in 5 weeks is a multiple of 7, and the total number of coins collected by B in 3 weeks is a multiple of 24, then the minimum possible number of coins collected by A in one week is [2023]

Ans: 42

Sol: Let the number of coins collected by A and B in one week be 3x and 4x respectfully.
 The total number of coins collected by A in 5 weeks = 15x
 For 15x to be a multiple of 7, x has to be a multiple of 7.
 The total number of coins collected by B in 3 weeks = 12x
 For 12x to be a multiple of 24, x has to be a multiple of 2.
 Therefore, x has to be a multiple of 7 × 2 = 14
 The minimum value that x can take is 14.
 So, the minimum coins collected by A in one week = 3x = 3 × 14 = 42.

2022

Q1: Pinky is standing in a queue at a ticket counter. Suppose the ratio of the number of persons standing ahead of Pinky to the number of persons standing behind her in the queue is 3 : 5. If the total number of persons in the queue is less than 300, then the maximum possible number of persons standing ahead of Pinky is  [2022]

Ans: 111

Sol: The ratio of the number of persons standing ahead of Pinky to the number of persons standing behind her in the queue is 3 : 5.

Let's assume that there are 3x number of people ahead of Pinky, then the number of people behind her will be 5x.

The total number of people in the queue is 8x + 1.

Since the total number of people in the queue is less than 300.

8x + 1 < 300

x ≤ 37

To find the maximum number of people ahead of Pinky, we take the maximum possible value of x, which is 37.

Therefore, the maximum number of people ahead of Pinky is 3 * 37 = 111

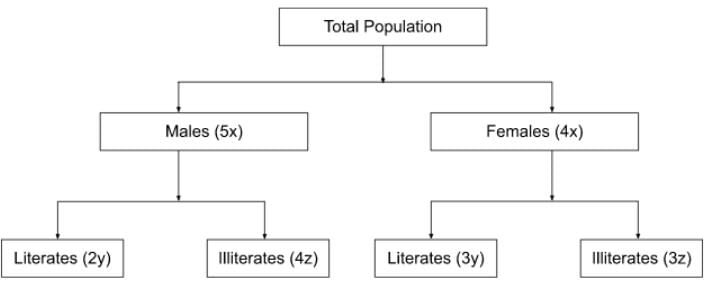
Q2: In a village, the ratio of number of males to females is 5 : 4. The ratio of number of literate males to literate females is 2 : 3. The ratio of the number of illiterate males to illiterate females is 4 : 3. If 3600 males in the village are literate, then the total number of females in the village is  [2022]

 Ans: 43200

Sol: The ratio of the number of males to females is 5 : 4
 The ratio of the number of literate males to literate females is 2 : 3.
 The ratio of the number of illiterate males to illiterate females is 4 : 3.
 Let,
 The number of males to females is 5x, 4x
 The number of literate males to literate females is 2y, 3y.
 The number of illiterate males to illiterate females is 4z, 3z.

 We know that the ratio of the number of males to females is 5 : 4

 4(2y + 4z) = 5(3y + 3z)
 8y + 16z = 15y + 15z
 z = 7y

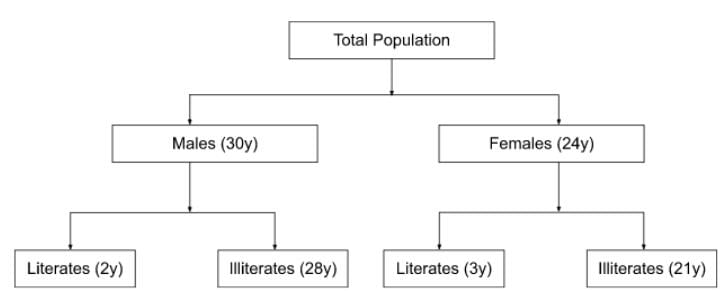
 3600 males in the village are literate.
 2y = 3600
 y = 1800
 Total number of females = 24y = 24(1800) = 43,200

Q3: In an election, there were four candidates and 80% of the registered voters casted their votes. One of the candidates received 30% of the casted votes while the other three candidates received the remaining casted votes in the proportion 1 : 2 : 3. If the winner of the election received 2512 votes more than the candidate with the second highest votes, then the number of registered voters was [2022]
(a) 40192
(b) 60288
(c) 50240
(d) 62800

Ans: d

Sol: One candidate got 30% of the polled votes, the remaining three got in the ratio of 1 : 2 : 3
 The polled votes were split in 3 : 7 ratio.
 The 70% of them were again split in the ratio 1 : 2 : 3
 The votes were polled in the ratio of 6(3) : 7(1 : 2 : 3)
 18 : 7 : 14 : 21
 Let's assume that the actual polled votes are 18x, 7x, 14x, 21x
 The winner of the election received 2512 votes more than the candidate with the second highest votes.
 21x - 18x = 2512
 3x = 2512
 Total polled votes = 18x + 7x + 14x + 21x = 60x = 20(3x) = 20(2512) = 50,240
 The polled votes represent 80% of the total registered votes.
 Total registered votes = 50,240 + 12,560 = 62,800.

Q4: A glass contains 500 cc of milk and a cup contains 500 cc of water. From the glass, 150 cc of milk is transferred to the cup and mixed thoroughly. Next, 150 cc of this mixture is transferred from the cup to the glass. Now, the amount of water in the glass and the amount of milk in the cup are in the ratio 
(a) 3 : 10
(b) 10 : 3
(c) 1 : 1
(d) 10 : 13

Ans: c
Sol:
The cup has 150 cc milk, 500 cc water and the glass has 350 cc milk after the 1^st transfer.
150 cc of mixture from glass will have milk and water in the ratio 3:10
After the 2^nd transfer, glass has (10/13)150 cc water and cup has 150 - (3/13)150 = (10/13)150
Ratio of both = 1 : 1

2021

Q1: The amount Neeta and Geeta together earn in a day equals what Sita alone earns in 6 days. The amount Sita and Neeta together earn in a day equals what Geeta alone earns in 2 days. The ratio of the daily earnings of the one who earns the most to that of the one who earns the least is 
(a) 3:2
(b) 11:7
(c) 11:3
(d) 7:3

Ans: c
Sol: Let the amounts Neeta, Geeta, and Sita earn in a day be n, g, and s respectively.
Then, it has been given that:
n+g=6s -i
s+n=2g -ii
ii-i, we get: s-g = 2g-6s
7s = 3g.
Let g be 7a. Then s earns 3a.
Then n earns 6s-g = 18a-7a = 11a.
Thus, the ratio is 11a:3a = 11:3

Q2: Anil, Bobby, and Chintu jointly invest in a business and agree to share the overall profit in proportion to their investments. Anil's share of investment is 70%. His share of profit decreases by ₹ 420 if the overall profit goes down from 18% to 15%. Chintu's share of profit increases by ₹ 80 if the overall profit goes up from 15% to 17%. The amount, in INR, invested by Bobby is 
(a) 2000
(b) 2400
(c) 2200
(d) 1800

Ans: a
Sol: Let the amount invested by Anil Bobby and Chintu be x, y, and z.
Considering x+y+z = 100*p.
Given Anil's share was 70 percent = 70*p.
As per the information provided : His share of profit decreases by ₹ 420 if the overall profit goes down from 18% to 15%.
Since the profits are distributed in the ratio of their investments : With a 3% decrease in the profits the value of profit earned by A decreased by Rs 420 which was 70 percent of the total invested.
Hence for all three of them would be combinedly losing

Hence 3 percent profit was equivalent to Rs 600.

The initial investment is equivalent to Rs 20000.
This is the total amount invested.
Chintu's profit share increased by Rs 80 when the profit percentage increased by 2 %. A 2 percent increase in profit is equivalent to Rs 20000*2/100 = Rs 400.
Of which Rs 80 is earned by Chintu which is 20% of the total Rs 400.
Hence he invested 20% of the total amount.
Bobby invested the other 10 percent.
10 percent of Rs 20000 = Rs 2000

Q3: A tea shop offers tea in cups of three different sizes. The product of the prices, in INR, of three different sizes is equal to 800. The prices of the smallest size and the medium size are in the ratio 2 : 5. If the shop owner decides to increase the prices of the smallest and the medium ones by INR 6 keeping the price of the largest size unchanged, the product then changes to 3200. The sum of the original prices of three different sizes, in INR, is 

Ans: 34
Sol: Let price of smallest cup be 2x and medium be 5x and large be y
Now by condition 1

Now as per second condition ;

Now dividing (2) and (1)

we get x=2

So 2x=4 and 5x=10
Now substituting in (1) we get y =20
Now therefore sum = 4+10+20 =34

2020

Q10: A sum of money is split among Amal, Sunil and Mita so that the ratio of the shares of Amal and Sunil is 3:2, while the ratio of the shares of Sunil and Mita is 4:5. If the difference between the largest and the smallest of these three shares is Rs 400, then Sunil's share, in rupees, is   [2020]

Ans: 800

Sol: Given ratio of shares of Amal and Sunil is 3: 2
 Also the ratio of shares of Sunil and Mita is 4: 5.
 Hence the ratio of shares of Anil, Sunil and Mita is 6: 4: 5
 ∴ Sunil's share = 400 x 4 / 2 = 800

Q2: The distance from B to C is thrice that from A to B. Two trains travel from A to C via B. The speed of train 2 is double that of train 1 while traveling from A to B and their speeds are interchanged while traveling from B to C. The ratio of the time taken by train 1 to that taken by train 2 in travelling from A to C is [2020]
(a) 1 : 4
(b) 7 : 5
(c) 5 : 7
(d) 4 : 1

Ans: c

Sol: Given,

 Let the speed of train 1 from A to B be s.
 Then the speed of train 2 from A to B is 2s.
Time taken by train 1 to cover A to C =
 And, time taken by train 2 to cover A to C
=
Required ratio =

2019

Q1: The salaries of Ramesh, Ganesh and Rajesh were in the ratio 6:5:7 in 2010, and in the ratio 3:4:3 in 2015. If Ramesh's salary increased by 25% during 2010-2015, then the percentage increase in Rajesh's salary during this period is closest to [2019] 
(a) 8
(b) 10
(c) 7
(d) 9

Ans: c

Sol: In 2010, Let the salary of Ramesh, Ganesh and Rajesh be 6x, 5x and 7x

Ramesh's salary increased by 25% during 2010 - 2015 = 6x × 125/100

⇒ 7.5x

But in 2015 the salaries ratio is 3 : 4 : 3 for Ramesh, Ganesh and Rajesh respectively

We can see in 2015, the salary of Ramesh and Rajesh is the same which is in the given ratio.

So, In 2015, the salary for Rajesh should also be 7.5x

Now percentage increase in the salary for Rajesh during 2010 - 2015 = [(7.5x - 7x)/7x] × 100

⇒ (0.5/7) × 100

⇒ 50/7

⇒ 7.14%

∴ The percentage increase in Rajesh's salary during this period is closest to 7%.

Q2: In an examination, Rama's score was one-twelfth of the sum of the scores of Mohan and Anjali. After a review, the score of each of them increased by 6. The revised scores of Anjali, Mohan, and Rama were in the ratio 11 : 10 : 3. Then Anjali's score exceeded Rama's score by [2019]
(a) 26
(b) 24
(c) 35
(d) 32

Ans: d

Sol: Since scores of Anjali, Mohan and Rama after review were in the ratio of 11 : 10 : 3, therefore we can suppose scores of Anjali, Mohan and Rama after review be 11x, 10x and 3x respectively.

Therefore, their scores before review was (11x - 6), (10x - 6) and (3x - 6) respectively.

Since, Rama's score was one-twelfth of the sum of the scores of Mohan and Anjali

⇒ 12 (3x - 6) = 21x - 12 ⇒ x = 4

Now, Anjali's score - Rama's score

= (11x - 6) - (3x - 6) = 8x = 8 × 4 = 32

Q3: The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is [2019]
(a) 13
(b) 14
(c) 12
(d) 15

Ans: b

Sol: Initial amount of salt in vessel A = 10 gms per 100 ml. solution. Therefore in 500 ml solution in vessel amount of salt = 50 gms

Similarly, initially in 500 ml solution in vessel B amount of salt = 110 gms

and initially in 500 ml solution in vessel C, amount of salt = 160 gms

When 100 ml is transferred from A to B, the amount of salt now in B = 10 + 110 = 120 gms in 600 ml.

The new concentration of salt in B = 120 / 600 x 100

= 20 gms per 100 ml.

Now, the amount of salt in A = 50 - 10 = 40 gms in 400 ml

Now, when 100 ml is transfered from B to C, the amount of salt now in C = 20 + 160 = 180 gms in 600 ml.

The new concentration of salt C = 180 / 600 x 100

= 30 gms per 100 ml

Finally, when 100 ml is transfered from C to A, the amount of salt now in A = 30 + 40 = 70 gms in 500 ml.

∴ Strength of salt in 70 / 500 x 100 = 14

Q4: A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is [2019]
(a) 75
(b) 85
(c) 80
(d) 70

Ans: c

Sol: Weight of liquid 1 per litre = 1000 gm

Weight of liquid 2 per litre = 800 gm

Weight of mixture per litre = 2 × 480 = 960 gm

By alligation rule,

Quantity of liquid 1 / Quantity of liquid 2 =  = 4 / 1

Hence, the liquids are mixed in 4 : 1.

∴ Percentage of liquid 1 = (4 / 4 + 1) x 100 = 80%

Q5: Amala, Bina, and Gouri invest money in the ratio 3 : 4 : 5 in fixed deposits having respective annual interest rates in the ratio 6 : 5 : 4. What is their total interest income (in Rs) after a year, if Bina's interest income exceeds Amala's by ₹ 250? [2019]
(a) 6000
(b) 7250
(c) 6350
(d) 7000

Ans: b

Sol: Ratio of incomes of Amala, Bina and Gouri = 3 : 4 : 5

Ratio of interests of Amala, Bina and Gouri = 6 : 5 : 4

Therefore, the ratio of their interest income = (3 × 6) : (4 × 5) : (5 × 4) = 18 : 20 : 20

Let the interest incomes of Amala, Bina and Gouri be 18x, 20x and 20x respectively.

Since, Bina's interest income exceeds Amala's by Rs 250

Therefore, 20x - 18x = 250 ⇒ x = 125

Total interest incomes = 18x + 20x + 20x = 58x = 58 × 125 = 7250

2018

Q1: Two types of tea, A and B, are mixed and then sold at Rs. 40 per kg. The profit is 10% if A and B are mixed in the ratio 3 : 2, and 5% if this ratio is 2 : 3. The cost prices, per kg, of A and B are in the ratio.  [2018]
(a) 17 : 25
(b) 21 : 25
(c) 18 : 25
(d) 19 : 24

Ans: d

Sol: Let the cost prices of A and B be Ca and Cb respectively.

Selling price of the mixture = 40 per kg.

The profit made is 10% if A and B are mixed in the ratio 3:2.

∴

⇒

The profit made is 5% if A and B are mixed in the ratio 2 : 3.

∴

⇒

Divide equation (i) by (ii), we get

⇒ 24Ca = 19Cb ⇒ Ca : Cb = 19 : 24

Q2: Raju and Lalitha originally had marbles in the ratio 4:9. Then Lalitha gave some of her marbles to Raju. As a result, the ratio of the number of marbles with Raju to that with Lalitha became 5:6. What fraction of her original number of marbles was given by Lalitha to Raju?  [2018]
(a) 6/19
(b) 7/33
(c) 1/4
(d) 1/3

Ans: b

Sol: Let the numbers of marbles with Raju and Lalitha be 4x and 9x respectively.

Let Lalitha gave y marbles to Raju.

∴  ⇒  

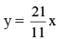
Fraction of original marbles that Lalitha gave to Raju

= y / 9x = 7 / 33

2017

Q1: A stall sells popcorn and chips in packets of three sizes : large, super, and jumbo. The numbers of large, super, and jumbo packets in its stock are in the ratio 7 : 17 : 16 for popcorn and 6 : 15 : 14 for chips. If the total number of popcorn packets in its stock is the same as that of chips packets, then the numbers of jumbo popcorn packets and jumbo chips packets are in the ratio  [2017]
(a) 1 : 1
(b) 8 : 7
(c) 4 : 3
(d) 6 : 5

Ans: a

Sol: Let the total no. of popcorn pockets in stock be T

Total no. of chips pockets in stock = T

Required ratio 

Q2: Suppose, C₁, C₂, C₃, C4 and C₅ are five companies. The profits made by C₁, C₂ and C₃ are in the ratio 9 : 10 : 8 while the profits made by C₂, C₄, and C₅ are in the ratio 18 : 19 : 20. If C₅ has made a profit of ₹19 crore more than C₁, then the total profit (in ₹) made by all five companies is  [2017]
(a) 438 crore
(b) 435 crore
(c) 348 crore
(d) 345 crore

Ans: a

Sol:
 

C₅ - C₁ = 19, the numbers above are the actual profits

∴ The total profit = 438 crore.