Projectile Motion - Class 11 PDF Download

A projectile is a body thrown into uniform gravitational field of earth (i.e. , near earth surface) which follows a path determined entirely by the effects of acceleration due to gravity and air resistance. In this section we will neglect the effects of air resistance and will assume that the acceleration due to gravity is constant throughout the trajectory of projectile. 

Analysis of Projectile Motion 

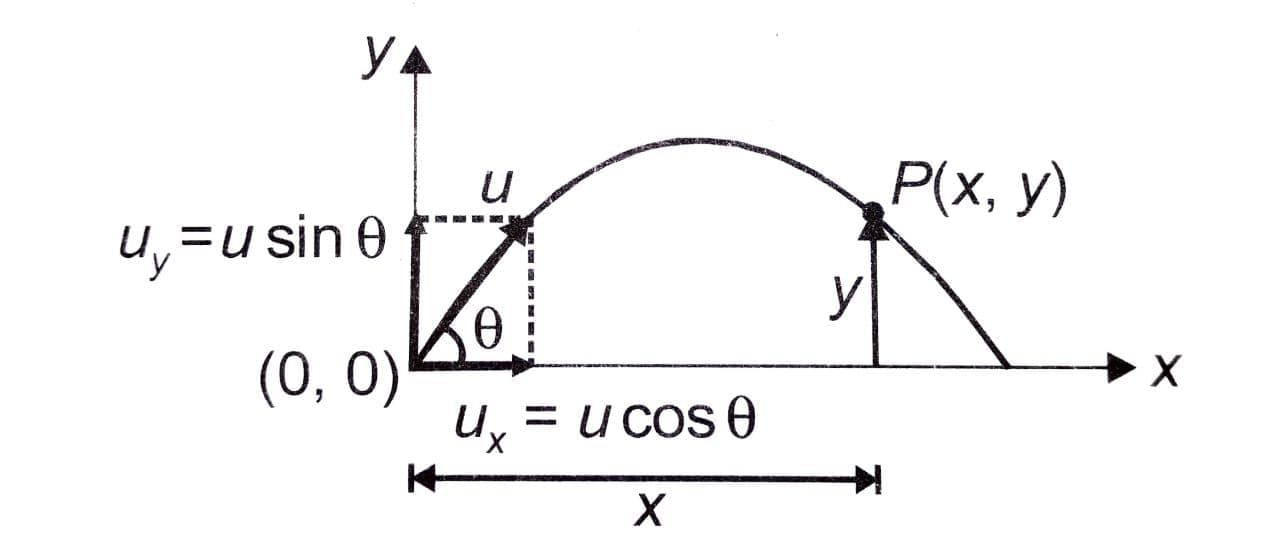
As the acceleration due to gravity is vertically downward, the projectile will always be confined in vertical plane. If  the projectile is thrown vertically upward the motion is one dimensional, and if the projectile is thrown inclined to the vertical, the motion is two-dimensional. Usually the xy-plane is chosen as the vertical plane of motion with y-axis along vertical and x-axis along horizontal direction. As the projectile moves on a curved path its position changes on both x and y axes. The analysis of motion is easier if we treat the x-direction motion and y-direction motion separately. The x-component of particle's acceleration is zero while the y-component of acceleration is constant and vertically downward. That is,   a_x = 0 and a_y = -g

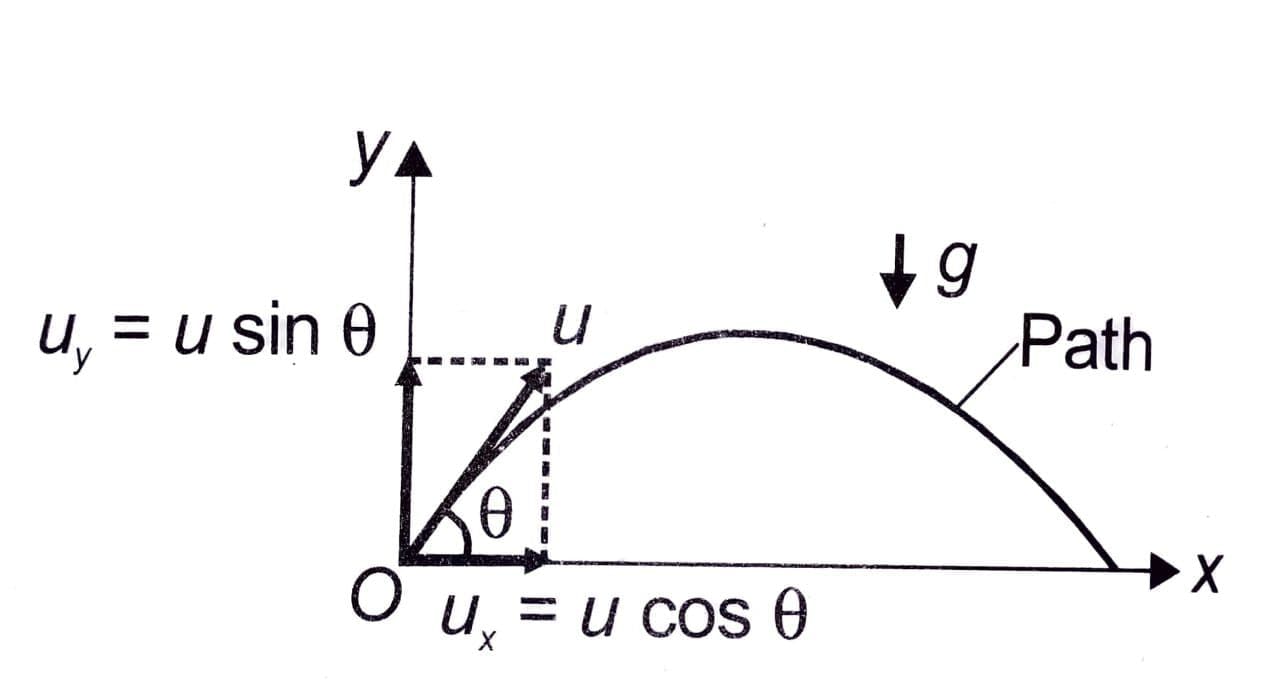
Although the motion is a uniformly accelerated motion but, it is easier to analyse the projectile motion as a combination of uniform motion in horizontal direction (a_x = 0) and uniformly accelerated motion in vertical direction (a_y = -g). Also the horizontal and vertical motions are independent of each other. i.e., neither motion affects the other.

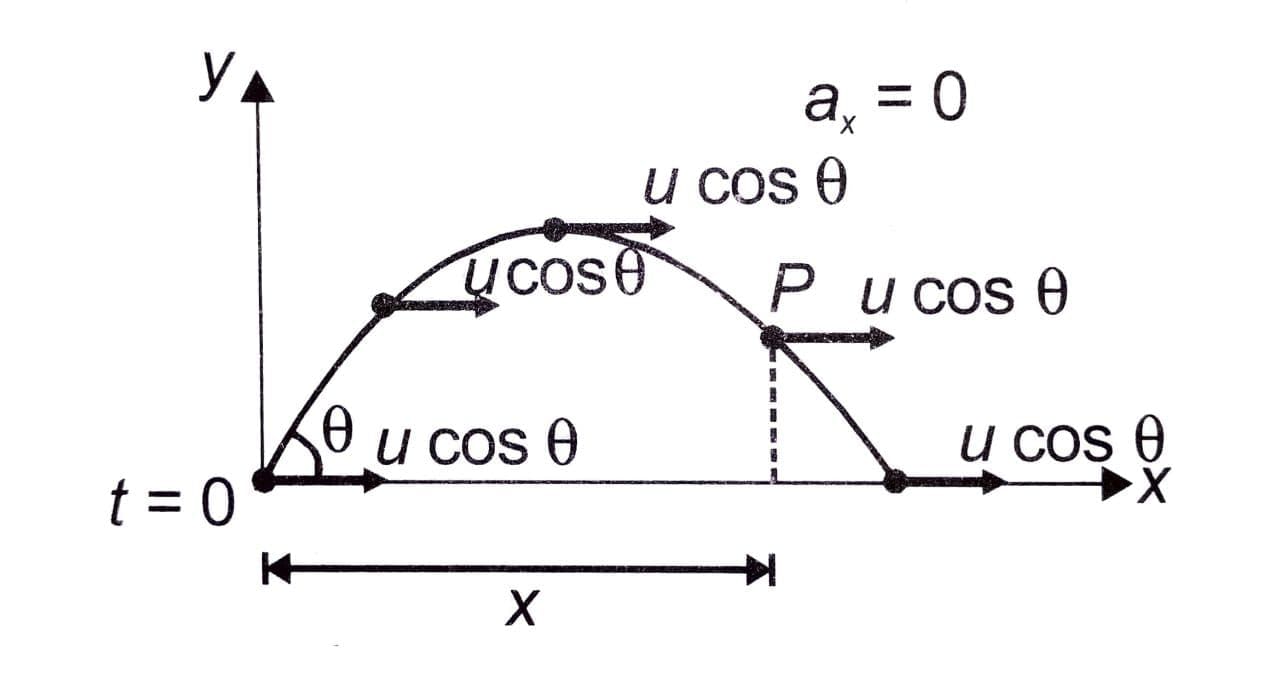
Horizontal Motion

If the projectile is thrown with speed u at an angle θ with horizontal, its initial horizontal velocity is ucosθ. Since a_x = 0 , the velocity ucosθ in horizontal direction remains constant at all time instants. If the particle reaches point P in time t, its horizontal displacement x is given by 

x = (ucosθ)t

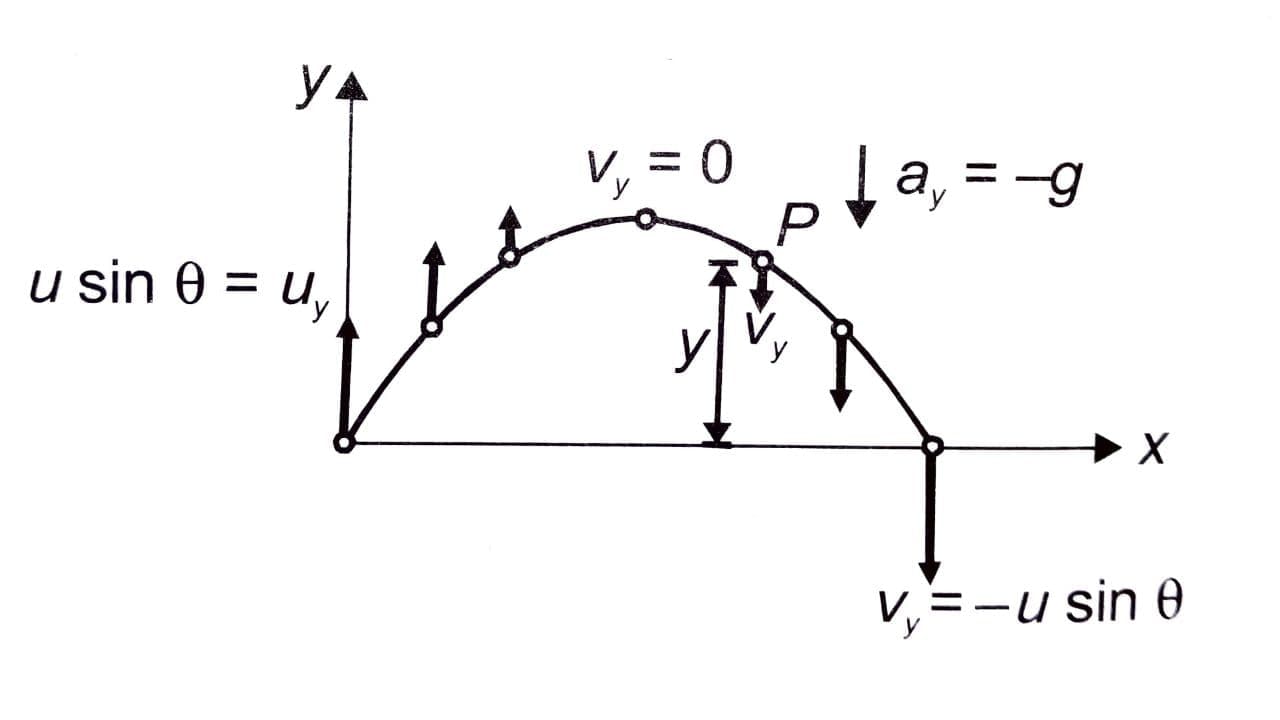
Vertical Motion 

There is a constant acceleration in vertically downward direction. The vertical velocity which is initially usinθ decreases and becomes zero at the topmost point. From then its magnitude increases in the downward direction. If the projectile reaches point P after time t, its vertical velocity and vertical displacement at that instant are given by 

v_y = usinθ - gt

y =  (usinθ)t - 1/2(gt²)

Equation of Trajectory

If x and y are the coordinates of particle after time t,

x = (ucosθ)t               -------- (i)

y = (usinθ )t - 1/2(gt²) ------- (ii)

From the equation (i) by putting the value of t as a function of x, in equation (ii) we get, 

y = xtanθ - gx²/2u²cos²θ

The above equation is called the equation of trajectory. As the equation represents a parabola the trajectory (or the path) of a projectile is a parabola. Here u, θ, x and y are four variables. if any three quantities, as mentioned, are known then the fourth quantity can be solved directly.

Time of Flight (T)

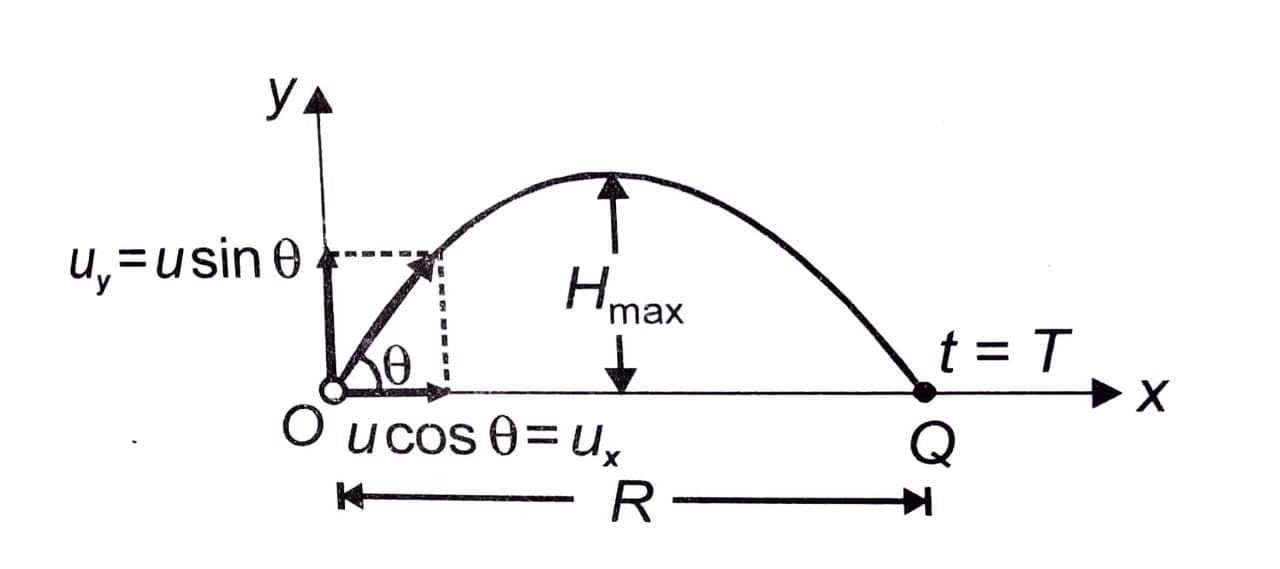
Let the projectile reach the point Q at t = T. At Q, y = 0 

⇒  0 = (usinθ)T - (1/2)gT²

⇒  T = 2usinθ/g

The time of flight can also be expressed as T = 2u_y/g , which shows that the time of flight depends only on the initial vertical velocity and is independent of horizontal motion.