Important Determinant Formulas Formulas for JEE and NEET
1.The symbol 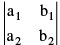 is called the determinant of order two.
is called the determinant of order two.
It's value is given by : D = a1 b2 − a2 b1
2.The symbol 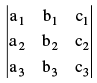 is called the determinant of order three.
is called the determinant of order three.
Its value can be found as : D = 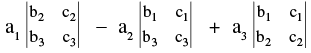
Or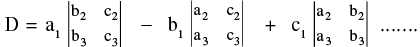 and so on. In this manner we can expand a determinant in 6 ways using elements of ; R1, R2, R3 or C1, C2, C3.
and so on. In this manner we can expand a determinant in 6 ways using elements of ; R1, R2, R3 or C1, C2, C3.
3. Following examples of short hand writing large expressions are :
(i) The lines : a1x + b1y + c1 = 0........ (1)
a2x + b2y + c2 = 0........ (2)
a3x + b3y + c3 = 0........ (3)
are concurrent if, 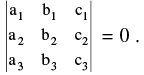 Condition for the consistency of three simultaneous linear equations in 2 variables.
Condition for the consistency of three simultaneous linear equations in 2 variables.
(ii) ax² + 2 hxy + by² + 2 gx + 2 fy + c = 0 represents a pair of straight lines if abc + 2 fgh − af² − bg² − ch² = 0 = 
(iii) Area of a triangle whose vertices are (xr, yr) ; r = 1 , 2 , 3 is : 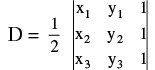 If D = 0 then the three points are collinear.
If D = 0 then the three points are collinear.
(iv) Equation of a straight line passing through 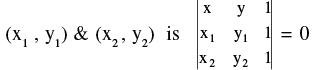
4. MINORS : The minor of a given element of a determinant is the determinant of the elements which remain after deleting the row & the column in which the given element stands For example, the minor of a1 in (Key Concept 2) is 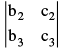 & the minor of b2 is
& the minor of b2 is
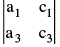 . Hence a determinant of order two will have “4 minors” & a determinant of order three will have “9 minors” .
. Hence a determinant of order two will have “4 minors” & a determinant of order three will have “9 minors” .
5. COFACTOR : If Mij represents the minor of some typical element then the cofactor is defined as :
Cij = (−1)i+j . Mij ; Where i & j denotes the row & column in which the particular element lies. Note that the value of a determinant of order three in terms of ‘Minor’ & ‘Cofactor’ can be written as : D = a11M11 − a12M12 + a13M13 OR D = a11C11 + a12C12 + a13C13 & so on .......
6. PROPERTIES OF DETERMINANTS :
P−1 : The value of a determinant remains unaltered, if the rows & columns are inter changed. e.g. if D = 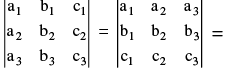 D′ D & D′ are transpose of each other. If D′ = − D then it is SKEW SYMMETRIC determinant but D′ = D ⇒ 2 D = 0 ⇒ D = 0 ⇒ Skew symmetric determinant of third order has the value zero.
D′ D & D′ are transpose of each other. If D′ = − D then it is SKEW SYMMETRIC determinant but D′ = D ⇒ 2 D = 0 ⇒ D = 0 ⇒ Skew symmetric determinant of third order has the value zero.
P−2 : If any two rows (or columns) of a determinant be interchanged, the value of determinant is changed in sign only. e.g. Let: 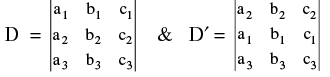 Then D′ = − D.
Then D′ = − D.
P−3 : If a determinant has any two rows (or columns) identical, then its value is zero. e.g. Let D =  then it can be verified that D = 0.
then it can be verified that D = 0.
P−4 : If all the elements of any row (or column) be multiplied by the same number, then the determinant is multiplied by that number.
e.g. If D 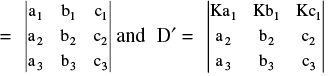 Then D′= KD
Then D′= KD
P−5 : If each element of any row (or column) can be expressed as a sum of two terms then the determinant can be expressed as the sum of two determinants. e.g. 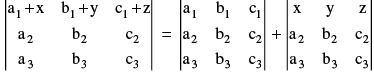
P−6 : The value of a determinant is not altered by adding to the elements of any row (or column) the same multiples of the corresponding elements of any other row (or column).e.g. Let D 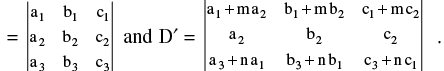 Then D′ = D.
Then D′ = D.
Note : that while applying this property ATLEAST ONE ROW (OR COLUMN) must remain unchanged.
P−7 : If by putting x = a the value of a determinant vanishes then (x − a) is a factor of the determinant.
7. MULTIPLICATION OF TWO DETERMINANTS : (i) 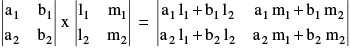 Similarly two determinants of order three are multiplied.
Similarly two determinants of order three are multiplied.
(ii) If D = 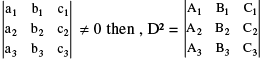 where Ai, Bi, Ci are cofactors
where Ai, Bi, Ci are cofactors
PROOF : Consider  Note : a1A2 + b1B2 + c1C2 = 0 etc. therefore,
Note : a1A2 + b1B2 + c1C2 = 0 etc. therefore, 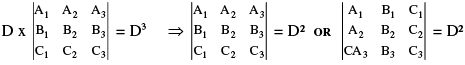
8. SYSTEM OF LINEAR EQUATION (IN TWO VARIABLES) :
(i) Consistent Equations : Definite & unique solution. [intersecting lines]
(ii) Inconsistent Equation : No solution. [Parallel line]
(iii) Dependent equation : Infinite solutions. [Identical lines]
Let a1x + b1y + c1 = 0 & a2x + b2y + c2 = 0 then :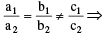 Given equations are inconsistent &
Given equations are inconsistent & 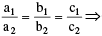 Given equations are dependent
Given equations are dependent
9. CRAMER'S RULE : [ SIMULTANEOUS EQUATIONS INVOLVING THREE UNKNOWNS]
Let, a1x + b1y + c1z = d1 ...(I) ; a2x + b2y + c2z = d2 ... (II) ; a3x + b3y + c3z = d3 ... (III)
Then, 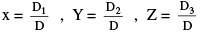 .
.
Where 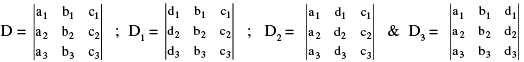
NOTE : (a) If D ≠ 0 and alteast one of D1, D2, D3 ≠ 0, then the given system of equations are consistent and have unique non trivial solution.
(b) If D ≠ 0 & D1 = D2 = D3 = 0, then the given system of equations are consistent and have trivial solution only.
(c) If D = D1 = D2 = D3 = 0, then the given system of equations are consistentand have infinite solutions. In case  represents these parallel planes then also D = D1 = D2 = D3 = 0 but the system is inconsistent.
represents these parallel planes then also D = D1 = D2 = D3 = 0 but the system is inconsistent.
(d) If D = 0 but at least one of D1, D2, D3 is not zero then the equations are in consistent and have no solution.
10. If x, y, z are not all zero, the condition for a1x + b1y + c1z = 0 ; a2x + b2y + c2z = 0 & a3x + b3y + c3z = 0 to be consistent in x, y, z is that 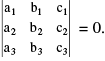 Remember that if a given system of linear equations have Only Zero Solution for all its variables then the given equations are said to have TRIVIAL SOLUTION.
Remember that if a given system of linear equations have Only Zero Solution for all its variables then the given equations are said to have TRIVIAL SOLUTION.
|
204 videos|290 docs|139 tests
|
FAQs on Important Determinant Formulas Formulas for JEE and NEET
| 1. What is the formula for calculating the determinant of a 2x2 matrix? |  |
| 2. How can I find the determinant of a 3x3 matrix using the cofactor expansion method? |  |
| 3. Is the determinant of a matrix affected by the row or column operations performed on it? |  |
| 4. What is the relationship between the determinant and the invertibility of a matrix? |  |
| 5. Can the determinant of a matrix be negative? |  |

|
Explore Courses for JEE exam
|

|

















