Important Differential Equations Formulas for JEE and NEET
Differential Equations Of First Order And First Degree
Definitions :
1. An equation that involves independent and dependent variables and the derivatives of the dependent variables is called a Differential Equations.
2. A differential equation is said to be ordinary , if the differential coefficients have reference to a single independent variable only and it is said to be PARTIAL if there are two or more independent variables . We are concerned with ordinary differential equations only. eg. 
= 0 is a partial differential equation.
3. Finding the unknown function is called solving or integrating the differential equation . The solution of the differential equation is also called its Primitive, because the differential equation can be regarded as a relation derived from it.
4. The order of a differential equation is the order of the highest differential coefficient occuring in it.
5. The degree of a differential equation which can be written as a polynomial in the derivatives is the degree of the derivative of the highest order occuring in it , after it has been expressed in a form free from radicals & fractions so far as derivatives are concerned, thus the differential equation : 
= 0 is order m & degree p. Note that in the differential equation ey′′′ − xy′′ + y = 0 order is three but degree doesn't apply.
6. Formation of a differential equation : If an equation in independent and dependent variables having some arbitrary constant is given , then a differential equation is obtained as follows: Differentiate the given equation w.r.t. the independent variable (say x) as many times as the number of arbitrary constants in it . Eliminate the arbitrary constants .
The eliminant is the required differential equation . Consider forming a differential equation for y² = 4a(x + b) where a and b are arbitary constant .
Note : A differential equation represents a family of curves all satisfying some common properties. This can be considered as the geometrical interpretation of the differential equation.
7. General And Particular Solutions : The solution of a differential equation which contains a number of independent arbitrary constants equal to the order of the differential equation is called the general solution (or complete integral or complete primitive) . A solution obtainable from the general solution by giving particular values to the constants is called a Particular solution.
Note that the general solution of a differential equation of the nth order contains ‘n’ & only ‘n’ independent arbitrary constants. The arbitrary constants in the solution of a differential equation are said to be independent, when it is impossible to deduce from the solution an equivalent relation containing fewer arbitrary constants. Thus the two arbitrary constants A, B in the equation y = A ex + B are not independent since the equation can be written as y = A eB. ex = C ex. Similarly the solution y = A sin x + B cos (x + C) appears to contain three arbitrary constants, but they are really equivalent to two only.
8. Elementary Types Of First Order & First Degree Differential Equations.
TYPE−−−−1. Variables separable : If the differential equation can be expressed as ; f (x)dx + g(y)dy = 0 then this is said to be variable − separable type.
A general solution of this is given by 
where c is the arbitrary constant . consider the example (dy/dx) = ex−y + x2. e−y.
Note : Sometimes transformation to the polar co−ordinates facilitates separation of variables.
In this connection it is convenient to remember the following differentials. If x = r cos θ ; y = r sin θ then,
(i) x dx + y dy = r dr
(ii) dx2 + dy2 = dr2 + r2 dθ2
(iii) x dy − y dx = r2 dθ If x = r sec θ & y = r tan θ then x dx − y dy = r dr and x dy − y dx = r2 sec θ dθ .
TYPE− 2 : 
To solve this , substitute t = ax + by + c. Then the equation reduces to separable type in the variable t and x which can be solved. Consider the
example 
TYPE− 3. Homogeneous equations
A differential equation of the form 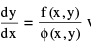 where f (x , y) & φ (x , y) are homogeneous functions of x & y , and of the same degree , is called Homogeneous .This equation may also be reduced to the form
where f (x , y) & φ (x , y) are homogeneous functions of x & y , and of the same degree , is called Homogeneous .This equation may also be reduced to the form 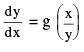
& is solved by putting y = vx so that the dependent variable y is changed to another variable v, where v is some unknown function, the differential equation is transformed to an equation with variables separable. Consider 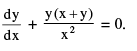
TYPE− 4. Equations reducible to the homogeneous form:
If 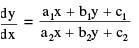 where a1 b2 − a2 b1 ≠ 0,
where a1 b2 − a2 b1 ≠ 0, 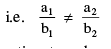
then the substitution x = u + h, y = v + k transform this equation to a homogeneous type in the new variables u and v where h and k are arbitrary constants to be chosen so as to make the given equation homogeneous which can be solved by the method as given in Type − 3.
If (i) a1 b2 − a2 b1 = 0 , then a substitution u = a1 x + b1 y transforms the differential
equation to an equation with variables separable. and
(ii) b1 + a2 = 0 , then a simple cross multiplication and substituting d (xy) for x dy + y dx & integrating term by term yields the result easily.
Consider 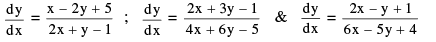
(iii) In an equation of the form : yf (xy) dx + xg (xy)dy = 0 the variables can be separated by the substitution xy = v.
Important note :
(a) The function f (x , y) is said to be a homogeneous function of degree n if for any real number t (≠ 0) , we have f (tx , ty) = tn f(x , y) .
For e.g. f(x , y) = ax2/3 + hx1/3 . y1/3 + by2/3 is a homogeneous function of degree 2/3
(b) A differential equation of the form 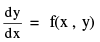 is homogeneous if f(x , y) is a homogeneous function of degree zero i.e. f(tx , ty) = t° f(x , y) = f(x , y). The function f does not depend on x & y separately but only on their ratio
is homogeneous if f(x , y) is a homogeneous function of degree zero i.e. f(tx , ty) = t° f(x , y) = f(x , y). The function f does not depend on x & y separately but only on their ratio 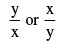
Linear diferential equations: A differential equation is said to be linear if the dependent variable & its differential coefficients occur in the first degree only and are not multiplied together The nth order linear differential equation is of the form 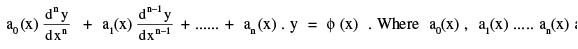
coefficients of the differential equation. Note that a linear differential equation is always of the first degree but every differental equation of the first degree need not be linear. e.g. the differential equation 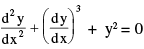 is not linear, though its degree is 1.
is not linear, though its degree is 1.
TYPE −−−− 5. Linear differential equations of first order :
The most general form of a linear differential equations of first order is 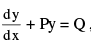
where P& Q are functions of x . To solve such an equation multiply both sides by 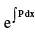
Note : (1) The factor 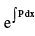 on multiplying by which the left hand side of the differential equation becomes the differential coefficient of some function of x & y , is called integrating factor of the differential equation popularly abbreviated as I. F.
on multiplying by which the left hand side of the differential equation becomes the differential coefficient of some function of x & y , is called integrating factor of the differential equation popularly abbreviated as I. F.
(2) It is very important to remember that on multiplying by the integrating factor , the left hand side becomes the derivative of the product of y and the I. F. (3) Some times a given differential equation becomes linear if we take y as the independent variable and x as the dependent variable. e.g. the equation ;
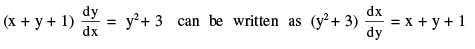 which is a linear differential
which is a linear differential
equation.
TYPE−−−−6. Equations reducible to linear form :
The equation 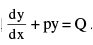 yn where P & Q functions of x , is reducible to the linear form by dividing it by yn & then substituting y−n+1 = Z . Its solution can be obtained as in Type−−−−5. Consider the example (x3 y2 + xy) dx = dy.
yn where P & Q functions of x , is reducible to the linear form by dividing it by yn & then substituting y−n+1 = Z . Its solution can be obtained as in Type−−−−5. Consider the example (x3 y2 + xy) dx = dy.
The equation 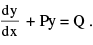 yn is called Bernouli’s equation.
yn is called Bernouli’s equation.
9. Trajectories: Suppose we are given the family of plane curves. Φ (x, y, a) = 0 depending on a single parameter a. A curve making at each of its points a fixed angle α with the curve of the family passing through that point is called an isogonal trajectory of that family ; if in particular α = π/2, then it is called an orthogonal trajectory.
Orthogonal trajectories : We set up the differential equation of the given family of curves. Let it be of the form F (x, y, y') = 0 The differential equation of the orthogonal trajectories is of the form F 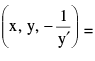 0 The general integral of this equation Φ1 (x, y, C) = 0 gives the family of orthogonal trajectories.
0 The general integral of this equation Φ1 (x, y, C) = 0 gives the family of orthogonal trajectories.
Note : Following exact differentials must be remembered :
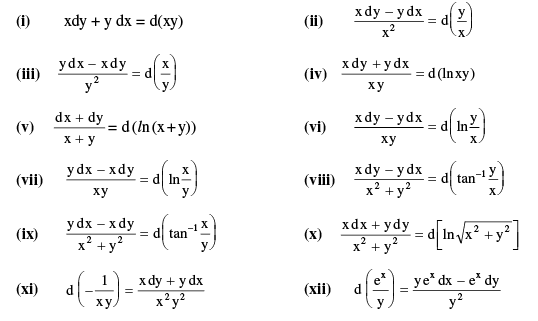
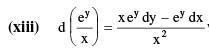
|
204 videos|290 docs|139 tests
|
FAQs on Important Differential Equations Formulas for JEE and NEET
| 1. What are the important formulas for solving differential equations? |  |
| 2. How do I solve a separable differential equation using the separation of variables method? |  |
| 3. What is Euler's formula for solving linear homogeneous differential equations with constant coefficients? |  |
| 4. How can I use the integrating factor formula to solve a linear first-order differential equation? |  |
| 5. What is a homogeneous linear differential equation and how can I solve it? |  |

|
Explore Courses for JEE exam
|

|

















