Sample Question Paper (2020-21) - 1 - Class 9 PDF Download
Class - IX
Mathematics
TIME: 3 Hrs.
M.M: 80
General Instructions:
1. This question paper contains two parts A and B.
2. Both Part A and Part B have internal choices.
Part – A
1. It consists of two sections - I and II.
2. Section I has 16 questions. Internal choice is provided in 5 questions.
3. Section II has four case study-based questions. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part – B
1. Question No 21 to 26 are Very short answer Type questions of 2 marks each.
2. Question No 27 to 33 are Short Answer Type questions of 3 marks each.
3. Question No 34 to 36 are Long Answer Type questions of 5 marks each.
4. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part - A
Section - I
Section I has 16 questions with 1 mark each. Internal choice is provided in 5 questions.
Q.1. Write a rational number between √2 and √3 (1 Mark)
OR
How many rational numbers are there between 13 and 17? (1 Mark)
Ans. We know that
√2 = 1.4142135.... and √3 = 1.732050807....
We see that 1.5 is a rational number which lies between 1.4142135….. and 1.732050807…
OR
Infinity Many,
Rational numbers are written in the form a / b where b ≠ 0; therefore, we can write infinitely many combinations of rational numbers between 13 and 17.
Q.2. Which of the following is irrational √4/9, √7? (1 Mark)
Ans. √4 / 9 = 2 / 3 which is a rational number.
√7 is an irrational number.
Q.3. Which one of the following is a polynomial? (1 Mark)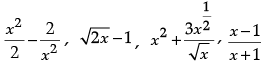
OR
How many zeros are there in the cubic equation? (1 Mark)
Ans. It is a polynomial because the degree of the polynomial is the whole number.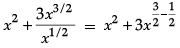
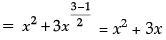
OR
Ans. 3 zeroes are there in a cubic equation.
Q.4. If (2, 0) is a solution of the linear equation 2x + 3y = k, then find the value of k. (1 Mark)
Ans. Put x = 2, y = 0 in the equation
2x + 3y = k
2 (2) + 3 (0) = k
4 + 0 = k
Hence, k = 4
Q.5. What is the ordinate of the points that lie on the x-axis? (1 Mark)
OR
In which quadrant, point (– 3, – 4) lies? (1 Mark)
Ans. Because ordinate or y-coordinate of a point is the perpendicular distance of this point from the x-axis measured along the y-axis. If a point lies on x-axis, then the perpendicular distance of a point from x-axis will be zero, so ordinate will be zero.
OR
Ans. 3rd quadrant
Q.6. The angles of a triangle are in the ratio 5 : 3 : 7. What is the type of triangle? (1 Mark)
Ans. Let the angles of triangle be 5x, 3x, 7x.
► According to question,
5x + 3x + 7x = 180° (angle sum property)
15x = 180° x = 11
I = 5 × 12 = 60°
II = 3 × 12 = 36°
III = 7 × 12 = 84°
∵ All the angles of the triangle are acute.
∵ The triangle is an acute-angled triangle.
Q.7. If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R, and of ∠D and ∠A at S, then PQRS is _______ whose opposite angles are _____. (1 Mark)
Ans. PQRS is a quadrilateral whose opposite angles are supplementary.
Q.8. ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140°, then find ∠BAC. (1 Mark)
Ans. Given that, ∠ADC + ∠ABC = 180°
140° + ∠ABC = 180
∠ABC = 180° – 140°
= 40°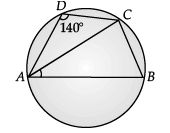
ABCD is a cyclic quadrilateral such that AB is the diameter of the circle circumscribing it.
Now, Join AC. ∠C = 90° [Angle in a semi-circle is a right angle]
In ∆ABC, we have
∠BAC = 180° – (90° + 40°) = 50°
Q.9. The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. What are the ratios of the surface areas of the balloon in the two cases? (1 Mark)
Ans. Radius r = 6cm
► Surface area = 3πr2 = 3π62 = 3π × 6 × 6
► Radius R = 12 cm
► Surface area = 3πR2 = 3π × 122
= 3π × 12 × 12
► Ratio = 3π × 6 × 6 : 3π × 12 × 12 = 1 : 4
Q.10. A coin is tossed 100 times with the following frequencies :
Head: 64, Tail: 36
Find the ratio of probabilities for each event. (1 Mark)
Ans.
► Total no. of outcomes = 100
► P (getting head) = 64 / 100
► P (getting tail) = 36 / 100
► Ratio = (64 / 100) : (36 / 100) = 64 : 36 = 16 : 9
Q.11. ∠A + ∠B + ∠C is in DABC = ________. (1 Mark)
OR
A ray has ___________ end point. (1 Mark)
Ans. Sum of measures of all the angles of a triangle is 180°.
OR
Ans. A ray has one endpoint. It is also called a fixed point.
Q.12. A coin is tossed 1000 times with the following frequencies of Head and Tail :
Head: 455, Tail: 545
Compute the probability for the events (i) getting a Head (ii) getting a Tail. (1 Mark)
Ans.
► Probability of getting head = 455 / 1200
= 91 / 240
► Probability of getting tail = 745 / 1200 = 149 / 240
Q.13. Bisector of an angle divides it in __________ equal parts. (1 Mark)
Ans. Two
Q.14. The angles of a quadrilateral are in the ratio 2:3:6:7. The largest angle of the quadrilateral is _____. (1 Mark)
Ans. Let the angles of the quadrilateral be 2x°, 3x°, 6x°, 7x°.
∴ 2x° + 3x° + 6x° + 7x° = 360°
[Angle sum property of quadrilateral]
or, 18x° = 360°
or, x° = 20°
∴ Largest angle = 7x° = 7 × 20° = 140°
Q.15. Write an example of a constant polynomial. (1 Mark)
OR
Name of the polynomial on the basis of degree. – 3x + 2. (1 Mark)
Ans. Constant polynomial is 7.
OR
Ans. Linear polynomial.
Q.16. In the given figure, PQ || RS and EF || QS. If ∠PQS = 60°, then what will be the measure of ∠RFE? (1 Mark)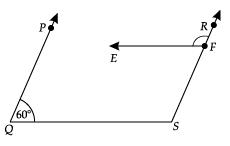 Ans. ∠PQS + ∠QSF = 180°
Ans. ∠PQS + ∠QSF = 180°
(Angles on the same side of transversal)
or, ∠PQS + ∠RFE = 180°, as ∠QSF = ∠EFR
or, 60° + ∠RFE = 180°(Corresponding angles)
∴ ∠RFE = 120°.
Section - II
Case study based questions are compulsory. Attempt any four sub-parts from each question. Each subpart carries 1 mark.
Q.17. Nikita has to make her project on 'Monument in India'. She decided to make her project on the Gol Gumbaz monument. She already knows the following things about it:
- It is located in a small town in Northern Karnataka.
- It reaches up to 51 meters in height while the giant dome has an external diameter of 44 meters, making it one of the largest domes ever built.
- At each of the four corners of the cube is a dome-shaped octagonal tower seven stories high with a staircase inside.

Help her in making the project by answering the following questions :
(i) What is the area of a cube? - 1 Mark
(a) lb + bh + hl
(b) 2(lb + bh + hl)
(c) 2(lb + bh)
(d) l2 + b2 + h2
Ans. (b)
(ii) What is the curved surface area of the hemispherical dome? - 1 Mark
(a) 908π m2
(b) 968π m2
(c) 340π m2
(d) 780π m2
Ans. (b)
Solution.
► Diameter = 44 m
► Radius = 22 m
► Curved surface area of hemispherical dome
= 2πr2
= 2π(22)2
= 968π m2
(iii) What is the height of the cubodial part? - 1 Mark
(a) 14 m
(b) 7 m
(c) 29 m
(d) 18 m
Ans. (c)
Solution.
► Total height of monument = 51 m
► Radius of hemispherical dome part
= height of hemispherical dome = 22 m
Height of the cuboidal part
= 51 m – 22m = 29 m
(iv) What is the circumference of the base of the dome? - 1 Mark
(a) 34π
(b) 22π
(c) 44π
(d) 55π
Ans. (c)
Solution.
► Circumference of the base of the dome = 2πr
= 2π(22) = 44π
(v) Find the cost of painting the dome, given the cost of painting is Rs. 100 per cm2. - 1 Mark
(a) Rs. 980π
(b) Rs. 9690π
(c) Rs. 968000π
(d) Rs. 9700π
Ans. (c)
Solution.
► Curved surface area of hemispherical dome
= 968p m2
► Cost of painting 100 cm2 = Rs. 10
► Cost of painting 1 m2 = Rs. 1000
Thus, cost of painting the dome
= Rs. 1000 × 968π cm2
= Rs. 968000
Q.18. Coronavirus disease (COVID-19) is an infectious disease. It is caused by a newly discovered coronavirus.
Most people who fall sick with COVID-19 experience mild to moderate symptoms and recover without special treatment.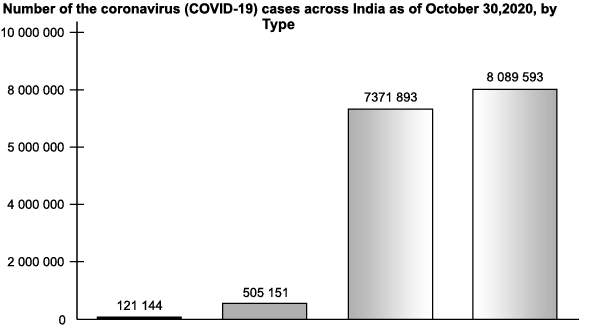
Coronavirus is mainly transmitted through droplets generated when an infected person coughs, sneezes, or exhales. Look at the bar graph and answer the following :
(i) What is a horizontal line representing? - 1 Mark
(a) Number of cases.
(b) Types of cases
(c) Number of people who died
(d) None of above
Ans. (a)
(ii) Which statement is correct? - 1 Mark
(a) Number of active cases is more than recovered cases.
(b) There is a little difference between deceased cases and confirmed cases.
(c) Recovery rate is very bad as compared to confirmed cases.
(d) Number of active cases is less than confirmed cases.
Ans. (d)
Solution.
The number of active cases is less than confirmed cases. This statement is correct. The number of active cases is very less as compared to confirmed cases. This shows people are recovering at a very high speed.
(iii) How many deceased cases were there as of October 30, 2020? - 1 Mark
(a) 595151
(b) 121144
(c) 7371898
(d) 8089593
Ans. (b)
(iv) How many confirmed cases were more than recovered cases? - 1 Mark
(a) 702310
(b) 770077
(c) 717695
(d) 782354
Ans. (c)
Solution.
Required number = confirmed cases – recovered cases
= 8089593 – 7371898
= 717695
(v) How many cases were active as of October 30, 2020? - 1 Mark
(a) 595151
(b) 121144
(c) 7371898
(d) 8089593
Ans. (a)
Q.19. Prime Minister's National Relief Fund (also called PMNRF in short) is the fundraised to provide support for people affected by natural and man-made disasters. Natural disasters that are covered under this include flood, cyclone, earthquake, etc. Man-made disasters that are included are major accidents, acid attacks, riots, etc.
Two friends Sita and Gita together contributed Rs. 200 towards Prime Minister's Relief Fund. Answer the following:
(i) Which out of the following is not the equation in two variables? [1 Mark]
(a) 2x = 3
(b) 4 = 5x – 4y
(c) x2 + x = 1
(d) x − √2y = 3
Ans. (a)
Solution.
x2 + x = 1 is not linear as highest power is 2.
Also, it is an equation in one variable.
Thus, it is not a linear equation in two variable
(ii) How to represent the above situation in linear equations in two variables? [1 Mark]
(a) 2x + y = 200
(b) x + y = 200
(c) 200x = y
(d) 200 + x = y
Ans. (b)
Solution.
Here, x represents Sita's contribution and y represents Gita's contribution
(iii) If Sita contributed Rs. 76, then how much was contributed by Gita? - 1 Mark
(a) Rs. 120
(b) Rs. 123
(c) Rs. 124
(d) Rs. 125
Ans. (c)
Solution.
f x = 76 then 76 + y = 200
y = 200 – 76
y = 124
(iv) If both contributed equally, then how much is contributed by each? - 1 Mark
(a) Rs. 50, Rs. 150
(b) Rs. 100, Rs. 100
(c) Rs. 50, Rs. 50
(d) Rs. 120, Rs. 120
Ans. (b)
Solution.
If x = y then x + x = 200
2x = 200
x = 200 / 2 = 100
Thus, each contribution is Rs. 100.
(v) Which is the standard form of linear equations x = – 5? [1 Mark]
(a) x + 5 = 0
(b) 1.x – 5 = 0
(c) 1.x + 0.y + 5 = 0
(d) 1.x + 0.y = 5
Ans. (d)
Solution:
Since, x = 5 ⇒ x + 5 = 0
Thus, standard form of x = – 5 is 1.x + 0.y + 5 = 0.
Q.20. During maths lab activity, the teacher gives four sticks of lengths 6 cm, 6 cm, 4 cm, and 4 cm to each student to make different types of quadrilateral.
She asks the following questions from the students:
(i) How many types of quadrilaterals can be possible? [1 Mark]
(a) 3
(b) 4
(c) 5
(d) 6
Ans. (a)
(iii) Write the name of the quadrilateral that can be formed with these sticks. [1 Mark]
(a) Kite, rectangle, rhombus
(b) Parallelogram, rectangle, trapezium
(c) Kite, rectangle, parallelogram
(d) Square, rectangle, kite
Ans. (c)
Solution.
Opposite sides of a parallelogram and a rectangle are equal. Also, adjacent sides of the kite are equal. Thus, kite, rectangle, and parallelogram can be formed with the sticks of lengths 6 cm, 6 cm, 4 cm, and 4 cm. Hence, the option (iii) is correct.
(iii) Which statement is incorrect? - 1 Mark
(a) Opposite sides of a parallelogram are equal
(b) A kite is not a parallelogram
(c) Diagonals of a parallelogram bisect each other
(d) A trapezium is a parallelogram
Ans. (d)
Solution.
A trapezium has only one pair of parallel sides. Thus, it cannot be a parallelogram.
(iv) A student formed a rectangle with these sticks. What is the length of the diagonal of the rectangle formed by the student? - 1 Mark
(a) 6√13cm
(b) 3√13cm
(c) √13 cm
(d) 2√13cm
Ans. (d)
Solution.
All the angles of a rectangle are the right angles. So, the diagonal of a rectangle divides it into two right-angled triangles. Thus,
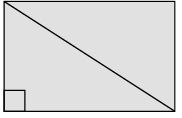 62 + 42 = l2
62 + 42 = l2
36 + 16 = l2
l2 = 52
l = 2√13cm
(v) A diagonal of a parallelogram divides it into two _______ triangles. - 1 Mark
(a) Similar
(b) Congruent
(c) Equilateral
(d) Right angled
Ans. (b)
Part – B
All questions are compulsory. In case of internal choice attempt anyone.
Q.21. If 7x = 1, then find the decimal expansion of x. (2 Mark)
Ans. x = 1 / 7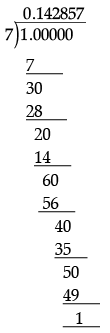
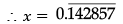 (CBSE Marking Scheme, 2012)
(CBSE Marking Scheme, 2012)
Q.22. If (3x – 15°) and (x + 5°) are complementary angles, find the angles. (2 Mark)
Ans. (3x – 15°) + (x + 5°) = 90°
or 4x = 90° + 10° = 100°
or x = 100° / 4
or, x = 25°
Angles are 60° and 30°.
OR
In the given figure, find the angles a and b and then show that LM || XY. (2 Mark)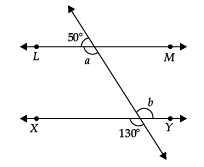 Ans. ∠a = 180° – 50°
Ans. ∠a = 180° – 50°
= 130° (Linear pair)
∠b = 130°
(Since Vertically opposite angles are equal)
This shows that ∠a = ∠b
But they are alternate interior angles,
∴ LM || XY (CBSE Marking Scheme, 2016)
Q.23. In the figure, ΔABC and ΔDBC are two isosceles triangles on the same base BC. Prove that ∠ABD = ∠ACD. (2 Mark)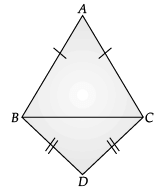 Ans.
Ans.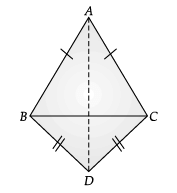
Join AD.
In ∆ABD and ∆ACD,
AB = AC (Given)
BD = CD (Given)
AD = AD (Common)
By using SSS Congruency Rule,
∆ABD ≅ ∆ACD
∴ ∠ABD = ∠ACD (CPCT)
Q.24. In the given figure, find the value of x. (2 Mark)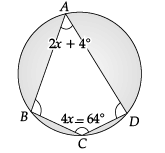 Ans. In a cyclic quadrilateral,
Ans. In a cyclic quadrilateral,
∠A + ∠C = 180°
(opposite angles of cyclic quadrilateral are supplementary)
or, 2x + 4° + 4x – 64° = 180°
or, 6x – 60° = 180°
or, 6x = 180° + 60° = 240°
or, x = 240° / 6
∴ x = 40°
Q.25. Draw any exterior angle of a triangle using a compass, bisect it. (2 Mark)
Ans.
Steps of construction:
- Construct a triangle ABC.
- Mark an exterior angle outside the triangle ABC and name the point as E.
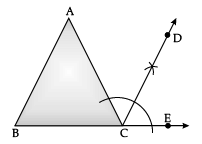
- Now, ACE is the exterior angle.
- Draw a bisector of ∠ACE.
OR
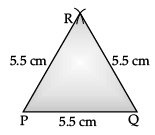
Construct an equilateral triangle PQR, when PQ = 5.5 cm. (2 Mark)
Ans.
Steps of construction:
- Draw any line segment PQ = 5.5 cm.
- With P as centre and radius 5.5 cm draw an arc.
- With Q as centre and radius 5.5 cm draw an arc to cut the previous arc at R.
- Join P R and QR, then PQR is the required triangle.
Q.26. Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm. (2 Mark)
Ans. Let the side AB(c) = 8 cm
Side AC(b) = 11 cm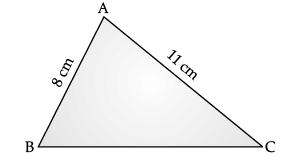
Perimeter of ∆ABC = 32 cm
a + b + c = 32 cm
a + 8 + 11 = 32
a = 32 – 19 = 13
∴ a = 13 cm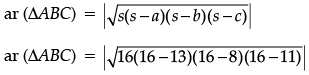
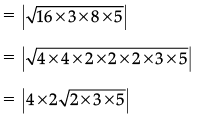
∴ ar (∆ABC) = 8√30 cm2
Q.27. Find three rational numbers between 5 / 7 and 9 / 11. (2 Mark)
Ans.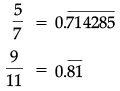
Hence three irrational numbers between 5 / 7 and 9 / 11 can be :
0·727227222...........
0·737337333...........
0·747447444........... (CBSE Marking Scheme, 2016)
OR
Express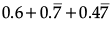 in the form p / q, where p and q are integers and q ≠ 0. (3 Mark)
in the form p / q, where p and q are integers and q ≠ 0. (3 Mark)
Ans. Let x = 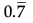 = 0.777... …(i)
= 0.777... …(i)
Multiply both sides by 10
10x = 7.777... …(ii)
Subtracting (i) from (ii),
9x = 7
x = 7 / 9
Let x = 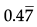 = 0.477... …(iii)
= 0.477... …(iii)
Multiply both sides of (iii) by 10
10x = 4.777... ...(iv)
Multiply both sides of (iv) by 10
100x = 47.777......(v)
Subtracting (iv) from (v),
90x = 43
x = 43 / 90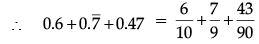
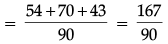
Q.28. Point A(4, 2), B(– 1, 2), and D(4, – 5) are three vertices of a rectangle ABCD. Plot these points and hence find the vertex C. (3 Mark)
Ans. From the graph, it is clear that the vertex of C(– 1, – 5)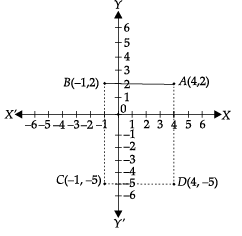 (CBSE Marking Scheme, 2016)
(CBSE Marking Scheme, 2016)
Q.29. If f(x) = x3 – 3x2 + 3x – 4, find f(2) + f(– 2) + f(0). (3 Mark)
Ans. Given, f(x) = x3 – 3x2 + 3x – 4
∴ f(2) = (2)3 – 3(2)2 + 3(2) – 4
= 8 – 12 + 6 – 4
f(2) = – 2
and f(– 2) = (– 2)3 – 3(– 2)2 + 3(– 2) – 4
= – 8 – 12 – 6 – 4
f(– 2) = – 30
and f(0) = – 4
∴ f(2) + f(– 2) + f(0) = – 2 – 30 – 4 = – 36
OR
Draw the quadrilateral ABCD whose vertices are A(0, 0), B(5, 0), C(3, 2) and D(0, 2). (3 Mark)
Ans.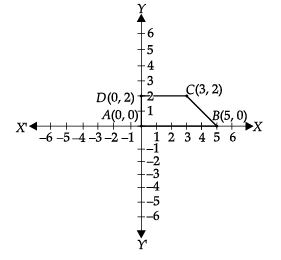 (CBSE Marking Scheme, 2016)
(CBSE Marking Scheme, 2016)
Q.30. Prove that if two lines intersect, vertically opposite angles are equal. (3 Mark)
Ans.
Given: Two lines AB and CD intersect at a point O. To Prove:
To Prove:
(i) ∠AOC = ∠BOD
(ii) ∠AOD = ∠BOC
Proof: ∴ Ray OA stands on line CD
∴ ∠AOC + ∠AOD = 180° [Linear pair] ...(i)
Again ray OD stands on line AB
∴ ∠AOD + ∠BOD = 180° [Linear pair]...(ii)
from eqn. (i) and (ii),
∠AOC + ∠AOD = ∠AOD + ∠BOD
[Each equal to 180°]
∴ ∠AOC = ∠BOD
Similarly ∠AOD = ∠BOC
(CBSE Marking Scheme, 2016)
Q.31. Find the area of a triangular field of sides 18 m, 24 m, and 30 m. Also, find the altitude corresponding to the shortest side. (3 Mark)
Ans.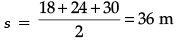
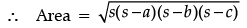
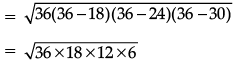
= 216 m2
∴ Altitude (Height) corresponding to the shortest side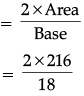
= 24 m.
Q.32. How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold? (Use π = 3.14) (3 Mark)
Ans. Given, diameter of hemispherical bowl = 10.5 cm
∴ Radius of hemispherical bowl
r = 10.5 / 2 = 5.25 cm
Volume of hemispherical bowl = 2 / 3 πr3
= 2 / 3 × 3.14 × (5.25)3
= 302.91
= 303 cm3
∴ Amount of milk that the hemispherical bowl can hold = 0.303 litres.
Q.33. ABCD is a rhombus. Show that the diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D. (3 Mark)
Ans. Given, ABCD is a rhombus.
So, AB = BC = CD = AD So, ∆ADC ≅ ∆ABC (By SSS Congruence Rule)
So, ∆ADC ≅ ∆ABC (By SSS Congruence Rule)
So, ∠DAC = ∠BAC (c.p.c.t.)
∠DCA = ∠BCA (c.p.c.t.) Hence Proved.
To prove : ∠BAC = ∠DAC and ∠DCA = ∠BCA
In ∆ADC and ∆ABC,
AB = AD (Given)
CD = CB (Given)
AC = AC (common)
Q.34. (a) The blood groups of 30 students of class IX are recorded as follows :
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
(i) Represent this data in the form of a frequency distribution table.
(ii) Which is the most common and which is the rarest blood group among these students
(b) Facts or information collected with a definite purpose are called: (5 Mark)
Ans. (a) (i) Frequency Distribution Table: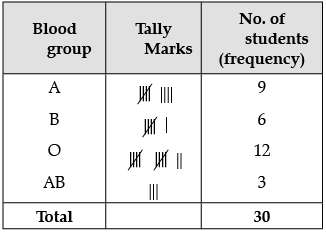 (ii) Blood group 'O' is most common as it has highest frequency i.e., 12. Blood group AB is rarest.
(ii) Blood group 'O' is most common as it has highest frequency i.e., 12. Blood group AB is rarest.
(b) Data
Q.35. Construct a DABC in which BC = 4.7 cm, ∠B = 45° and AB – AC = 2 cm. (5 Mark)
Ans.
Steps of construction:
- Draw a line segment BC = 4.7 cm and at point, B construct an angle of 45° i.e., ∠XBC = 45°.
- Cut the line segment BD = 2 cm (equal to AB – AC) on ray BX.
- Join DC and draw the perpendicular bisector PQ of DC.
- The perpendicular bisector intersects BX at point A. Join AC. ∆ABC is the required triangle.
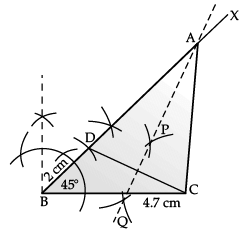 (CBSE Marking Scheme, 2016)
(CBSE Marking Scheme, 2016)
OR
A student Amit of class IX is unable to write in his examination, due to a fracture in his arm. Akhil a student of class VI writes for him. The sum of their ages is 25 years.
(i) Write a linear equation for the above situation and represent it graphically.
(ii) Find the age of Akhil from the graph, when the age of Amit is 14 years. (5 Mark)
Ans. Let Age of Amit = x years
Age of Akhil = y years
(i) According to the question the linear equation for the above situation is
x + y = 25
or, y = 25 – x
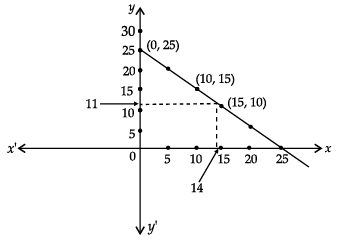 (ii) From the graph when Amit’s age = 14 years, then Akhil’s age = 11 years.
(ii) From the graph when Amit’s age = 14 years, then Akhil’s age = 11 years.
Q.36. In-class IX of 50 students, second language opted by the students is as follows:
Sanskrit – 14
Japanese – 08
French – 12
Urdu – 6
Rest of them opted for German.
A student is selected at random. Find the probability that the student.
(i) opts for French
(ii) does not opts for Japanese
(iii) Either opts for Sanskrit or for German. (5 Mark)
Ans. (i) Probability that a student selected opts
French language = 12 / 50
= 6 / 25
(ii) Probability that a student selected does not opt for Japanese = 1 – selected student opts Japanese
= 1 - 8 / 50
= 42 / 50 = 21 / 25
(iii) Probability that selected student either opts for Sanskrit or for German = Probability. of student opts Sanskrit + Probability of student opts. German
∵ Number of student who opted German
= 50 – (14 + 08 + 12 + 6)
= 50 – 40 = 10
∴ Probability that selected student either opt for Sanskrit or for German
= 14 / 50 = 10 / 50
= 24 / 50 = 12 / 25
FAQs on Sample Question Paper (2020-21) - 1 - Class 9
| 1. What is the structure of the question paper for Class 9 exams? |  |
| 2. How many sections are there in Part A of the Class 9 exam question paper? |  |
| 3. What is the purpose of Part B in the Class 9 exam question paper? |  |
| 4. How should the FAQs and answers be related to the given article in Section II of Part A? |  |
| 5. Are there any specific guidelines for the complexity of the questions and answers in Section II of Part A? |  |















