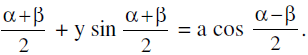Important Conic Section Formulas for JEE and NEET
1. Equation Of A Circle In Various Form :
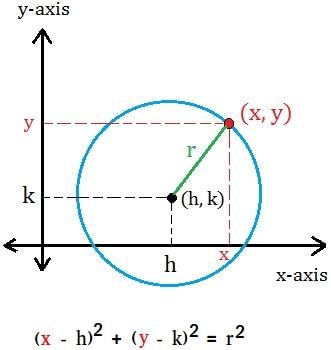
(a) The circle with centre(h, k) & radius ‘r’ has the equation:
(x − h)² + (y − k)² = r²
(b) The general equation of a circle is
x² + y² + 2gx + 2fy + c = 0 with centre as :
Remember that every second degree equation in x & y in which coefficient of x² = coefficient of y² & there is no xy term always represents a circle.
If g² + f ² − c > 0 ⇒ real circle.
g² + f ² - c = 0 ⇒ point circle.
g² + f ² - c < 0 ⇒ imaginary circle.
Note that the general equation of a circle contains three arbitrary constants, g, f & c which corresponds to the fact that a unique circle passes through three non collinear points.
(c) The equation of circle with (x1 , y1) & (x2 , y2) as its diameter is :
(x − x1) (x − x2) + (y − y1) (y − y2) = 0.
Note that this will be the circle of least radius passing through (x1 , y1) & (x2 , y2).
2. Intercepts Made By A Circle On The Axes :
The intercepts made by the circle x² + y² + 2gx + 2fy + c = 0 on the co-ordinate axes are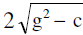 &
&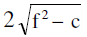 respectively.
respectively.
Note :
If g² − c > 0 ⇒ circle cuts the x axis at two distinct points.
If g² = c ⇒ circle touches the x-axis.
If g² < c ⇒ circle lies completely above or below the x-axis.
3. Position Of A Point w.r.t. A Circle :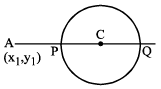 The point (x1 , y1) is inside, on or outside the circle x² + y² + 2gx + 2fy + c = 0.
The point (x1 , y1) is inside, on or outside the circle x² + y² + 2gx + 2fy + c = 0.
according as x1² + y1² + 2gx1 + 2fy1 + c ⇔ 0 .
Note : The greatest & the least distance of a point A from a circle with centre C & radius r is AC + r & AC − r respectively.
4. Line & A Circle :
Let L = 0 be a line & S = 0 be a circle.
If r is the radius of the circle & p is the length of the perpendicular from the centre on the line, then :
(i) p > r ⇔ the line does not meet the circle i. e. passes out side the circle.
(ii) p = r ⇔ the line touches the circle.
(iii) p < r ⇔ the line is a secant of the circle.
(iv) p = 0 ⇒ the line is a diameter of the circle.
5. Parametric Equations Of A Circle :
The parametric equations of (x − h)² + (y − k)² = r² are :
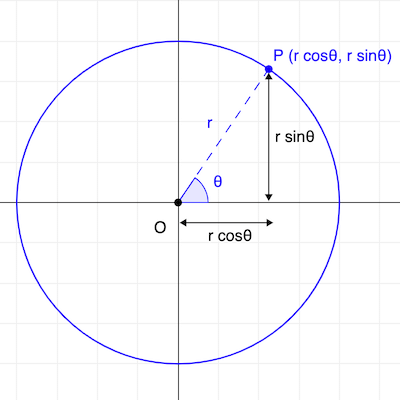
x = h + r cos θ ; y = k + r sin θ ; − π < θ ≤ π where (h, k) is the centre,r is the radius & θ is a parameter.
Note that equation of a straight line joining two point α & β on the circle x² + y² = a² is x cos
6. Tangent & Normal :
(a) The equation of the tangent to the circle x² + y² = a² at its point (x1 , y1) is, x x1 + y y1 = a².
Hence equation of a tangent at (a cos α, a sin α) is ;
x cos α + y sin α = a. The point of intersection of the tangents at the points P(α) and Q(β) is 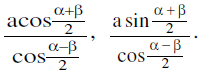
(b) The equation of the tangent to the circle x² + y² + 2gx + 2fy + c = 0 at its point (x1 , y1) is
xx1 + yy1 + g (x + x1) + f (y + y1) + c = 0.
(c) y = mx + c is always a tangent to the circle x² + y² = a² if c² = a² (1 + m²) and the point of contact is 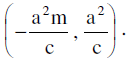
(d) If a line is normal / orthogonal to a circle then it must pass through the centre of the circle. Using this fact normal to the circle x² + y² + 2gx + 2fy + c = 0 at (x1 , y1) is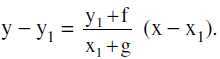
7. A Family Of Circles :
(a) The equation of the family of circles passing through the points of intersection of two circles S2 = 0 & S2 = 0 is :
S1 + K S2 = 0 (K ≠ −1).
(b) The equation of the family of circles passing through the point of intersection of a circle S = 0 & a line L = 0 is given by
S + KL = 0.
(c) The equation of a family of circles passing through two given points (x1 , y1) & (x2 , y2) can be written in the form :
(x − x1) (x − x2) + (y − y1) (y − y2) + K 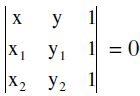
where K is a parameter.
(d) The equation of a family of circles touching a fixed line y − y1 = m (x − x1) at the fixed point (x1 , y1) is (x − x1)²+ (y − y1)² + K [y − y1 − m (x − x1)] = 0
where K is a parameter.
In case the line through (x1 , y1) is parallel to y - axis the equation of the family of circles touching it at (x1 , y1) becomes
(x − x1)²+ (y − y1)² + K (x − x1) = 0.
Also if line is parallel to x - axis the equation of the family of circles touching it at (x1, y1) becomes
(x − x1)²+ (y − y1)² + K (y − y1) = 0.
(e) Equation of circle circumscribing a triangle whose sides are given by L1 = 0 ; L2 = 0 & L3 = 0 is given by ;
L1L2 + λ L2L3 + μ L3L1 = 0
provided co-efficient of xy = 0 & co-efficient of x² = co-efficient of y².
(f) Equation of circle circumscribing a quadrilateral whose side in order are represented by the lines L1 = 0, L2 = 0, L3 = 0 & L4 = 0 is L1L3 + l L2L4 = 0 provided co-efficient of x² = co-efficient of y² and co-efficient of xy = 0.
8. Length Of A Tangent And Power Of A Point :
The length of a tangent from an external point (x1 , y1) to the circle S ≡ x² + y² + 2gx + 2fy + c = 0 is given by 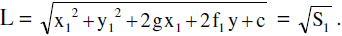 Square of length of the tangent from the point P is also called THE POWER OF POINT w.r.t. a circle. Power of a point remains constant w.r.t. a circle.
Square of length of the tangent from the point P is also called THE POWER OF POINT w.r.t. a circle. Power of a point remains constant w.r.t. a circle.
Note that : power of a point P is positive, negative or zero according as the point ‘P’ is outside, inside or on the circle respectively.
9. Director Circle :
The locus of the point of intersection of two perpendicular tangents is called the Director Circle of the given circle. The director circle of a circle is the concentric circle having radius equal to √2 times the original circle.
10. Equation Of The Chord With A Given Middle Point :
The equation of the chord of the circle S ≡ x² + y² + 2gx + 2fy + c = 0 in terms of its mid point M (x1,y1) is y − y1 = 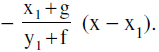
This on simplifying can be put in the form xx1 + yy1 + g (x + x1) +f (y + y1) + c = x1² + y1² + 2gx1 + 2fy1 + c which is designated by T = S1.
Note that : the shortest chord of a circle passing through a point ‘M’ inside the circle, is one chord whose middle point is M.
11. Chord Of Contact :
If two tangents PT1 & PT2 are drawn from the point P (x1, y1) to the circle S ≡ x² + y²+ 2gx + 2fy + c = 0, then the equation of the chord of contact T1T2 is : xx1 + yy1 + g (x + x1) + f (y + y1) + c = 0.
Remember :
(a) Chord of contact exists only if the point ‘P’ is not inside .
(b) Length of chord of contact T1 T2 = 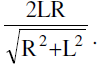
(c) Area of the triangle formed by the pair of the tangents & its chord of contact = 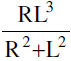 Where R is the radius of the circle & L is the length of the tangent from (x1, y1) on S = 0.
Where R is the radius of the circle & L is the length of the tangent from (x1, y1) on S = 0.
(d) Angle between the pair of tangents from (x1, y1) = tan−1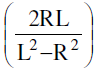 where R = radius ; L = length of tangent.
where R = radius ; L = length of tangent.
(e) Equation of the circle circumscribing the triangle PT1 T2 is :
(x − x1) (x + g) + (y − y1) (y + f) = 0.
(f) The joint equation of a pair of tangents drawn from the point A (x1 , y1) to the circle x² + y² + 2gx + 2fy + c = 0 is :
SS1 = T².
Where S ≡ x² + y² + 2gx + 2fy + c ; S1 ≡ x1²+ y1²+ 2gx1+ 2fy1 + c T ≡ xx1 + yy1 + g(x + x1) + f(y + y1) + c.
12. Pole & Polar :
(i) If through a point P in the plane of the circle , there be drawn any straight line to meet the circle in Q and R, the locus of the point of intersection of the tangents at Q & R is called the Polar of the point P ; also P is called the Pole of the Polar.
(ii) The equation to the polar of a point P (x1 , y1) w.r.t. the circle x² + y²= a² is given by xx1 + yy1 = a², & if the circle is general then the equation of the polar becomes xx1 + yy1 + g (x + x1) + f (y + y1) + c = 0. Note that if the point (x1 , y1) be on the circle then the chord of contact, tangent & polar will be represented by the same equation.
(iii) Pole of a given line Ax + By + C = 0 w.r.t. any circle x² + y² = a² is 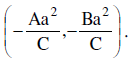
(iv) If the polar of a point P pass through a point Q, then the polar of Q passes through P.
(v) Two lines L1 & L2 are conjugate of each other if Pole of L1 lies on L2 & vice versa Similarly two points P & Q are said to be conjugate of each other if the polar of P passes through Q & vice-versa.
13. Common Tangents To Two Circles :
(i) Where the two circles neither intersect nor touch each other , there are FOUR common tangents, two of them are transverse & the others are direct common tangents.
(ii) When they intersect there are two common tangents, both of them being direct.
(iii) When they touch each other :www.MathsBySuhag.com , www.TekoClasses.com
(a) Externally : there are three common tangents, two direct and one is the tangent at the point of contact .
(b) Internally : only one common tangent possible at their point of contact.
(iv) Length of an external common tangent & internal common tangent to the two circles is given by: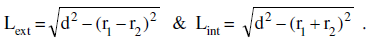
Where d = distance between the centres of the two circles . r1 & r2 are the radii of the 2 circles.
(v) The direct common tangents meet at a point which divides the line joining centre of circles externally in the ratio of their radii. Transverse common tangents meet at a point which divides the line joining centre of circles internally in the ratio of their radii.
14. Radical Axis & Radical Centre :
The radical axis of two circles is the locus of points whose powers w.r.t. the two circles are equal. The equation of radical axis of the two circles S1 = 0 & S2 = 0 is given ;
S1 − S2 = 0 i.e. 2 (g1 − g2) x + 2 (f1 − f2) y + (c1 − c2) = 0.
Note That :
(a) If two circles intersect, then the radical axis is the common chord of the two circles.
(b) If two circles touch each other then the radical axis is the common tangent of the two circles at the common point of contact.
(c) Radical axis is always perpendicular to the line joining the centres of the 2circles.
(d) Radical axis need not always pass through the mid point of the line joining the centres of the two circles.
(e) Radical axis bisects a common tangent between the two circles.
(f) The common point of intersection of the radical axes of three circles taken two at a time is calledthe radical centre of three circles.
(g) A system of circles , every two which have the same radical axis, is called a coaxal system.
(h) Pairs of circles which do not have radical axis are concentric.
15. Orthogonality Of Two Circles :
Two circles S1= 0 & S2= 0 are said to be orthogonal or said to intersect orthogonally if the tangents at their point of intersection include a right angle. The condition for two circles to be orthogonal is :
2 g1 g2 + 2 f1 f2 = c1 + c2 .
Note :
(a) Locus of the centre of a variable circle orthogonal to two fixed circles is the radical axis between the two fixed circles .
(b) If two circles are orthogonal, then the polar of a point 'P' on first circle w.r.t. the second circle passes through the point Q which is the other end of the diameter through P . Hence locus of a point which moves such that its polars w.r.t. the circles S1 = 0 , S2 = 0 & S3 = 0 are concurrent in a circle which is orthogonal to all the three circles.
|
172 videos|503 docs|154 tests
|
FAQs on Important Conic Section Formulas for JEE and NEET
| 1. What is the formula for the circumference of a circle? |  |
| 2. How do you find the area of a circle using the formula? |  |
| 3. What is the relationship between the diameter and radius of a circle? |  |
| 4. How can you find the radius of a circle if you are given the diameter? |  |
| 5. Can you find the circumference of a circle without knowing the radius? |  |