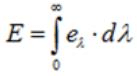Heat Transfer - Practice Revision Notes | Basic Technology for JSS 1 PDF Download

➢ Conduction

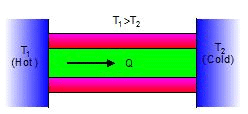
• Conduction is that mode of transmission of heat by which heat travels, through an unequally heated body, from the hot end to the cold end, from particle to particle, the particles themselves remaining at their mean positions.
  

➢ Convection

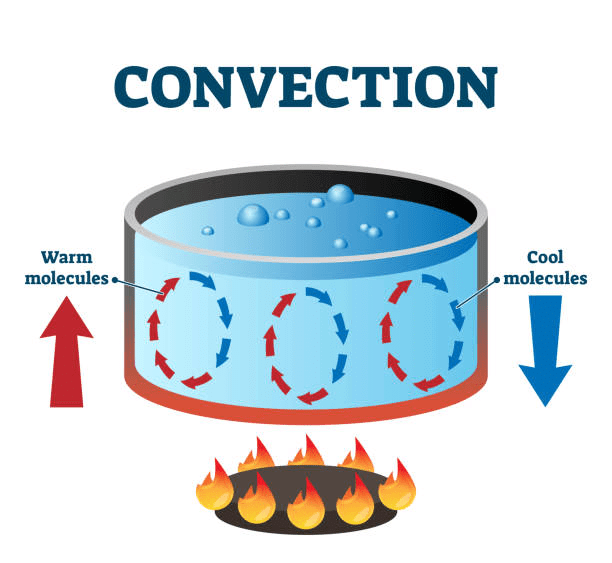
• It is the mode of transmission of heat, through fluids, in which the particle of fluids acquire heat from one region and deliver the same to the other regions by leaving their mean positions and moving from one point to another.

➢ Radiation

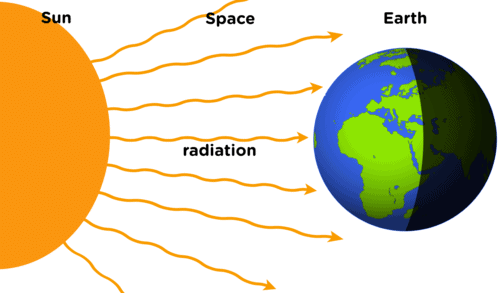
• It is defined as that mode of transmission of heat in which heat travels from hot body to cold body in straight lines without heating the intervening medium.

View Answer  

Power, 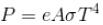Here, σ is the Stefan’s constant.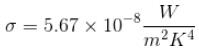

➢ Temperature Gradient

•  It is defined as the rate of change of temperature of different cross-section with distance.

➢ Coefficient of Thermal Conductivity

• Rate of flow of heat = dQ/dt
• Heat current, through a conducting rod, is defined as the amount of heat conducted across any cross-section of the rod in one second.
  H= dQ/dt

H depends upon following factors:

(a) Area of cross-section of rod: H ∝ A
(b) Temperature Gradient: H ∝-dθ/dx
(c)  Nature of the material

So, H = -KA (dθ/dx)
Here K is called the coefficient of thermal conductivity of the material of rod. It depends upon the nature of material of rod.

(d) The total heat Q crossing from one cross-section to the other in time t.

Q = KA(θ₁-θ₂)t/l
Or K = Ql/A(θ₁-θ₂)t

Coefficient of thermal conductivity of the material of a rod is defined as the heat current (amount of heat flowing per second) flowing per unit area between two cross-section of the rod each of area 1m² and separated 1m apart.

Dimension of K:
[K] = [M¹L¹T^-3K^-1]
Unit: C.G.S- cal cm^-1s^-1 ºC^-1
S.I.: Wm^-1K^-1

➢ Thermal Conductance (σ_h) 

• It is defined as heat current per unit temperature difference.

View Answer  

σ_h= KA/l
σ_h= H/dθ

Unit- S.I- WK^-1

➢ Thermal Resistance (R_H)

• Thermal resistance of a conductor is defined as the temperature difference between its two cross-sections when a unit heat current flows through it.
• Reciprocal of thermal conductance is known as thermal resistance of the substance.

View Answer  

R_h= 1/σ_H = l/KA = dθ/H

Units of R_H: S.I – W^-1K

➢ Analogy between Electricity and Heat

• H= (θ₁- θ₂)/(l/KA) = (θ₁- θ₂)/R_h

➢ Searle’s Method for K

• K= m(θ₄- θ₃)d/A(θ₁- θ)t
• The ratio of thermal and electrical conductivities is the same for the metals at a particular temperature and is proportional to the absolute temperature of the metal. If T is the absolute temperature, then
  K/σ ∝ T or K/ σT = constant

➢  Ingen Hausz Experiment

• K₁/K₂ = l₁²/ l₂²
• Thermal resistance of a conductor of length d:  R_TH = d/KA

Flow of a heat through a composite slab:
(a) Thermal Resistance in Series: Thermal resistance of the composite slab is equal to the sum of their individual thermal resistances.

(l₁ +l₂)/KA = (l₁/K₁A) + (l₂/K₂A)
R_comb = R_h+R_h'
If l₁=l₂=l, then, K = 2K₁K₂/K₁+K₂

Temperature of the interface:

θ₀= [θ₁R_h' + θ₂R_h]/ [R_h+ R_h'] or θ₀ 
= [θ₁K₁l₂+ θ₂ K₂l₁]/ [K₁l₂+ K₂l₁]

(b) Thermal resistance in parallel: Reciprocal of the combination thermal resistance is equal to the sum of the reciprocals of individual thermal resistances.
1/R_comb = 1/R_h + 1/R_h

➢ Bolometer

• If R_t and R₀ are the resistances of the conductor at 0ºC and tºC, then, R_t = R₀(1+αt), Here α is the temperature coefficient of change of resistance with temperature.

➢ Absorptive Power (a)

• Absorptive power (a) of the substance is defined as the ratio between amounts of heat absorbed by it to the total amount of heat incident upon it.
  a = Q₁/Q

➢ Reflecting Power (r)

• Reflecting power (r) of a substance is defined as the ratio between amount of heat reflected by the substance to the total amount of heat incident upon it.
  r= Q₂/Q

➢ Transmitting Power (t)

• Transmitting power (t) of a substance is defined as the ratio between amount of heat transmitted by the body to the total amount of heat incident upon it.

t = Q₃/Q
a + r + t = Q₁/Q + Q₂/Q + Q₃/Q = [Q₁+ Q₂+ Q₃]/Q = Q/Q = 1

➢ Radiant Emittance (E) 

• Radiant emittance of a body at a temperature T is defined as the total amount of energy (for all wavelengths) radiated per unit time, per unit area by the body.

Unit: S.I-Jm^-2s^-1
C.G.S: erg cm^-2s^-1

➢ Energy Density

• Total energy density (U) at any point is defined as the radiant energy per unit volume, around that point, for wave-lengths taken together.    

 
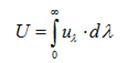
➢ Kirchhoff’s Law of Heat Radiation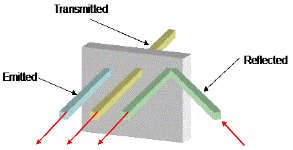

• It states that at any temperature, the ratio of emissive power e_λ of a body to its absorptive power a_λ, for a particular wave-length, is always constant and is equal to the emissive power of perfect black body for that wavelength.
• e_λ/a_λ = Constant = E_λ
• This implies the ratio between e_λ and a_λ for any body is a constant quantity (=E_λ).

➢ Wein’s Displacement Law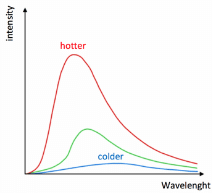

• It states that wavelength of radiation which is emitted with maximum intensity varies inversely as the absolute temperature of the body.
• λ_m×T = Constant

➢ Stefan’s Law 

• Radiant emittance or the energy radiated per second per unit area by a perfect black body varies directly as the fourth power of its absolute temperature.
• E = σT⁴
• Here σ is the Stefan’s constant and its value is 5.735×10^-8 Wm^-2K^-4

➢ Spectral Emissive Power

• e_λ= Q/At(dλ)

➢ Emissivity 

• ε = e/E,  0 ≤ ε ≤1
• The emissivity of a body is numerically equal to its absorptive power.
  e = a_λ
• Emissivity of body determines the radiant emittance of a body.
• Emissivity of a perfect body is always one.
• Emissivity of any body other than a perfect black body is less than one.
• Emissivity of any body is numerically equal to its absorbing power.

➢ Rate of Loss of Heat 

• -dQ/dT = εAσ(θ⁴- θ₀⁴)
• For spherical objects:
  (dQ/dT)₁/(dQ/dT)₂ = r₁²/r₂²

➢ Newton’s Law of Cooling 

• It states that the rate of loss of heat of a body is directly proportional to the temperature difference between the body and surroundings.
• dQ/dt = -K(T-T₀) or (T-T₀) ∝ e^-KT

➢ Wein’s Radiation Law 

• E_λdλ = (A/λ⁵) f(λT) dλ = (A/λ⁵) e^-a/λT dλ

➢ Solar Constant 

• S = (R_S/R_ES)² σT⁴