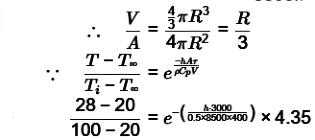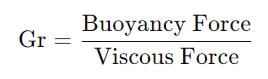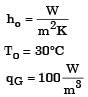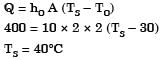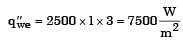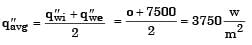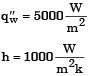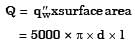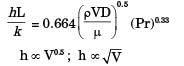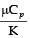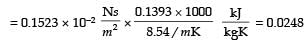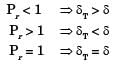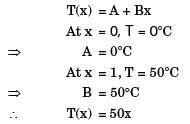Q1: Consider a hydrodynamically and thermally fully-developed, steady fluid flow of 1 kg/s in a uniformly heated pipe with diameter of 0.1 m and length of 40 m. A constant heat flux of magnitude 15000 W/m2 is imposed on the outer surface of the pipe. The bulk-mean temperature of the fluid at the entrance to the pipe is 200°C. The Reynolds number (Re ) of the flow is 85000, and the Prandtl number ( Pr ) of the fluid is 5. The thermal conductivity and the specific heat of the fluid are 0.08 W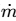 −1
−1 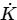 −1 and 2600 J
−1 and 2600 J 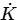 g−1
g−1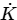 − 1, respectively. The correlation Nu = 0.023 Re 0.8 Pr 0.4 is applicable, where the Nusselt Number (Nu) is defined on the basis of the pipe diameter. The pipe surface temperature at the exit is ________ °C (round off to the nearest integer). [GATE ME 2022, SET-2]
− 1, respectively. The correlation Nu = 0.023 Re 0.8 Pr 0.4 is applicable, where the Nusselt Number (Nu) is defined on the basis of the pipe diameter. The pipe surface temperature at the exit is ________ °C (round off to the nearest integer). [GATE ME 2022, SET-2]
Ans: (317 to 324)
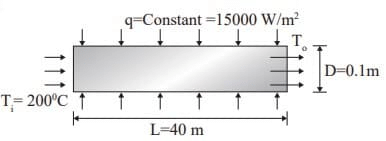
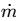 = 1kg/ sec
= 1kg/ sec
Re = 85000
Pr = 5
K = 0.08W/mK
C = 2600j/kgK
Nu = 0.023 Re 0.8 Pr 0.4
Nu = hD/k
Ts = ?
1500 x π x 0.1 x 40 = 1 x 2600 x (T0 - 200)
To = 275.5°C
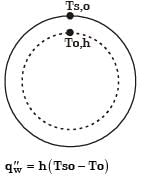
Newtons law of cooling
q = h (Ts - Tm)
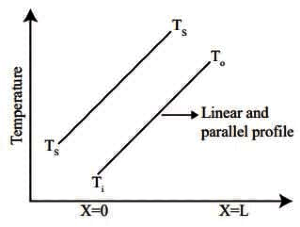
Q2: Which of the following non-dimensional terms is an estimate of Nusselt number? [GATE ME 2022 SET-2]
(a) Ratio of internal thermal resistance of a solid to the boundary layer thermal resistance
(b) Ratio of the rate at which internal energy is advected to the rate of conduction heat transfer
(c) Non-dimensional temperature gradient
(d) Non-dimensional velocity gradient multiplied by Prandtl number
Ans: (c)
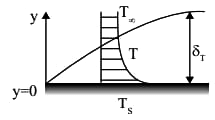 θ* = (Ts - T) / (Ts - T∞)
θ* = (Ts - T) / (Ts - T∞)
y* = y / L
dy */dy = 1/L
dθ*/dy = -dT/dy
Ts and T∞ are constant
At boundary
q conduction = q convection

Applying chain rule
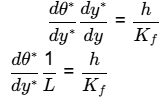
dθ*/dy* = hL / Kf = Nusselt Number
Nu = dθ*/dy*
Nu represents non dimensional temperature gradient.
Q3: In forced convective heat transfer, Stanton number (St), Nusselt number (Nu), Reynolds number (Re) and Prandtl number (Pr) are related as [GATE ME 2021, SET-2]
(a) St = Nu/Re Pr
(b) St = Nu Re/ Pr
(c) St =Nu Pr Re
(d) Nu Re/Pr
Ans: (a)
St = Nu/Re Pr
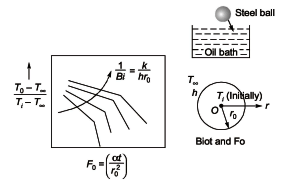
Q4: A hot steel spherical ball is suddenly dipped into a low temperature oil bath.
Which of the following dimensionless parameters are required to determine instantaneous center temperature of the ball using a Heisler chart? [GATE ME 2021 SET-1]
(a) Biot number and Fourier number
(b) Reynolds number and Prandtl number
(c) Biot number and Froude number
(d) Nusselt number and Grashoff number
Ans: (a)
Q5: Water flows through a tube of 3 cm internal diameter and length 20 m, The outside surface of the tube is heated electrically so that it is subjected to uniform heat flux circumferentially and axially. The mean inlet and exit temperatures of the water are 10 °C and 70°C, respectively. The mass flow rate of the water is 720 kg/h. Disregard the thermal resistance of the tube wall. The internal heat transfer coefficient is 1697 W/m2. Take specific heat Cp of water as 4.179 kJ/kg. K. The inner surface temperature at the exit section of the tube is __________ °C(round off to one decimal place). [GATE ME 2020, SET-2]
Ans: (85.1 to 86.1)
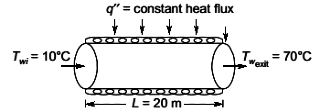
h=1697W/m 2 K
From energy balance equation,
Heat flux × Area of HT
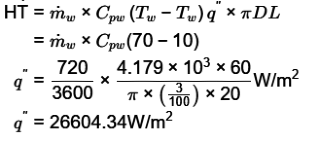 Applying Newton's law of cooling at exit
Applying Newton's law of cooling at exit
q" = h x (Ttube at exit - T water at exit) W/m2
266604.34 = 1697 x (Ttube at exit - 70) W/m2
(Ttube at exit = 85.67°C
Q6: A small metal bead (radius 0.5 mm), initially at 100°C , when placed in a stream of fluid at 20°C, attains a temperature of 28°C in 4.35 seconds. The density and specific heat of the metal are 8500 k g/m3 and 400 J/kgK, respectively. If the bead is considered as lumped system, the convective heat transfer coefficient (in W/m2K ) between the metal bead and the fluid stream is [GATE ME 2020, SET-1]
(a) 283.3
(b) 299.9
(c) 149.9
(d) 449.7
Ans: (b)
r = 0.5mm; cp = 400j/kg; p = 8500kg/m3; t = 4.35sec
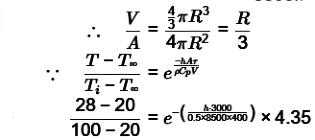
⇒ h = 299.95W/m2K
Question for GATE Past Year Questions: Free & Forced Convection
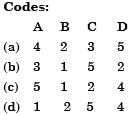
Try yourself:Match List-I with List-ll and select the correct answer using the code given below the lists:
List-I
A. Grashof number
B. Schmidt number
C. Weber number
D. Fourier number
List-II
1. Mass diffusion
2. Transient heat conduction
3. Free convection
4. Forced convection
5. Surface tension
6. Radiation
[1996]
Explanation
-
Grashof Number (A): The Grashof number is used in fluid dynamics to describe free convection. It relates the buoyancy forces to the viscous forces within a fluid. In simpler terms, it helps in analyzing the flow of fluid when there are temperature differences causing movement.
Matches with: 3 (Free convection)
-
Schmidt Number (B): The Schmidt number is a dimensionless number used in fluid dynamics that describes the ratio of momentum diffusivity (viscosity) to mass diffusivity. It is important in mass transfer operations.
Matches with: 1 (Mass diffusion)
-
Weber Number (C): The Weber number is a dimensionless number in fluid mechanics that is used to analyze the relative importance of the fluid's inertia compared to its surface tension. It is commonly used in the study of droplets, bubbles, and liquid surfaces.
Matches with: 5 (Surface tension)
-
Fourier Number (D): The Fourier number is a dimensionless number used in heat conduction problems. It represents the ratio of heat conduction rate to the rate of heat storage, making it crucial in transient heat conduction analysis.
Matches with: 2 (Transient heat conduction)
The correct matching code is (b) 3, 1, 5, 2,
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:The ratio of momentum diffusivity (v) to thermal diffusivity (α), is called
[2015]
Explanation
The ratio of momentum diffusivity (ν) to thermal diffusivity (α) is called the Prandtl number.
-
Prandtl Number (Pr): This is a dimensionless number that represents the ratio of momentum diffusivity (kinematic viscosity, ν) to thermal diffusivity (α). It is used to relate the relative thickness of the momentum boundary layer to the thermal boundary layer in fluid flow.
-
Nusselt Number (Nu): It represents the ratio of convective to conductive heat transfer across a boundary.
-
Biot Number (Bi): It relates the internal resistance to heat conduction within a body to the external convective heat transfer.
-
Lewis Number (Le): This is the ratio of thermal diffusivity to mass diffusivity.
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:Grashof number signifies the ratio of
[2016]
Explanation
The Grashof number signifies the ratio of buoyancy force to viscous force in a fluid.
Grashof Number (Gr): It is a dimensionless number that compares the relative significance of buoyancy forces to viscous forces in fluid flow. It is important in the study of natural convection, where fluid motion is caused by temperature-induced density differences (buoyancy).
A high Grashof number indicates that buoyancy forces dominate, leading to strong natural convection.
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:In pool boiling the highest HTC occurs in
[1990]
Explanation
The highest Heat Transfer Coefficient (HTC) in pool boiling occurs in the nucleate boiling zone.
-
Nucleate Boiling Zone: This is the regime where small bubbles form on the heated surface and then detach into the liquid. The heat transfer is extremely efficient in this zone because the bubbles enhance the mixing of the liquid, thus increasing the heat transfer rate significantly.
-
Subcooled Boiling Zone: This occurs when the bulk liquid is at a temperature below its boiling point, so boiling happens only near the surface. The HTC here is lower compared to nucleate boiling.
-
Partial Film Boiling Zone: In this zone, part of the surface is covered by a vapor film, which reduces heat transfer because vapor has lower thermal conductivity than liquid.
-
Film Boiling Zone: In this zone, the surface is completely covered by a stable vapor film, which significantly lowers the heat transfer coefficient due to the insulating effect of the vapor.
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:Heat transfer coefficients for free convection in gases, forced convection in gases and vapours, and for boiling water lie, respectively, in the range of
[1998]
Explanation
The heat transfer coefficients for free convection in gases, forced convection in gases and vapours, and for boiling water lie, respectively, in the range of:
- Free convection in gases: 5-15 W/m²K
- Forced convection in gases and vapours: 20-200 W/m²K
- Boiling water: 3000-50000 W/m²K
Explanation:
-
Free convection in gases: Heat transfer by natural or free convection in gases has a relatively low heat transfer coefficient because the fluid movement is primarily due to buoyancy forces.
-
Forced convection in gases and vapours: In forced convection, the movement of gases is induced by external forces (e.g., a fan or pump), leading to a higher heat transfer coefficient compared to free convection.
-
Boiling water: Boiling water has a significantly higher heat transfer coefficient due to the phase change from liquid to vapor, which enhances heat transfer.
Correct Answer:
A: 5-15; 20-200 and 3000-50000 W/m²K
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
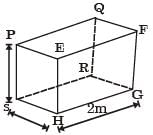
Try yourself:For the three-dimensional object shown in the figure below, five faces are insulated. The sixth face (PQRS), which is not insulated, interacts thermally with the ambient, with a convective heat transfer coefficient of 10W/m2K. The ambient temperature is 30°C. Heat is uniformly generated inside the object at the rate of 100 W/m3. Assuming the face PQRS to be at uniform temperature, its steady state temperature is
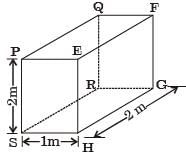
[2000]
Explanation
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:Water (specifie heat, c = 4.18 kJ/kgK) enters a pipe at a rate 0.01 kg/s and a temperature of 20°C. The pipe, of diameter 50 mm and length 3 m, is subjected to a wall heat flux q"w in W/m2.
If q"w = 2500x, where x is in m and in the direction of flow (x = 0 at the inlet), the bulk means temperature of the water leaving the pipe in °C is
[2013]
Explanation
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:Water (specifie heat, c = 4.18 kJ/kgK) enters a pipe at a rate 0.01 kg/s and a temperature of 20°C. The pipe, of diameter 50 mm and length 3 m, is subjected to a wall heat flux q"w in W/m2.
If q"w = 5000 and the convection heat transfer coefficient at the pipe outlet is 1000 W/m2K, the temperature in °C at the inner surface of the pipe at the outlet is
[2013]
Explanation
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:For laminar forced convection over a flat plate, if the free stream velocity increases by a factor of 2, the average heat transfer coefficient
[2014]
Explanation
Forlaminar flow, Nu = 0.664 (Re)0.5 (Pr)0.33
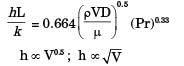
So when free stream velocity increases by a factor of 2, then the average heat transfer coefficient rises by a factor of √2.
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:The properties of mercury at 300 K are: Density = 13529 kg/m3, cp = 0.1393 kJ/kgK, dynamic viscosity = 0.1523 × 10–2 Ns/m2 and thermal conductivity = 8.540 W/mK. The Prandtl number of the mercury at 300 K is
[2002]
Explanation
Prandtl number = 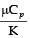
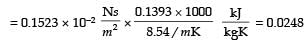
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:In the laminar flow of air (Pr = 0.7) over a heated plate, if δ and δT denote, respectively, the hydrodynamic and thermal boundary layer thicknesses, then
[2015]
Explanation
When
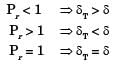
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:For a hydrodynamically and thermally fully developed laminar flow through a circular pipe of constant cross-section. The Nusselt number at constant wall heat flux (Nuq) and that at constant wall temperature (NuT) are related as
[2019]
Explanation
(Nu)q for constant wall heat flux and (Nu)T at constant wall temperature for a hydrodynamically and thermally fully developed laminar flow through a circular pipe of constant cross-section is 4.36 and 3.66 respectively.
Report a problem
Question for GATE Past Year Questions: Free & Forced Convection
Try yourself:The wall of a constant diameter pipe of length 1 m is heated uniformly with flux q” by wrapping a heater coil around it. The flow at the inlet to the pipe is hydrodynamically fully developed. The fluid is incompressible and the flow is assumed to be laminar and steady all through the pipe.
The bulk temperature of the fluid is equal to 0°C at the in let and 50°C at the exit. The wal l temperatures are measured at three locations, P, Q an d R as shown in the figure. The flow thermally develops after some distance from the inlet. The following measurements are made :
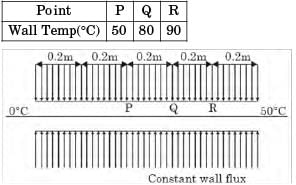
Among the locations P, Q and R, the flow is thermally at :
[2019]
Explanation
In case of uniform heat flux, bulk mean temperature varies linearly. The difference between bulk mean temperature and wall temperature is constant in thermally developed region so bulk tempeature,
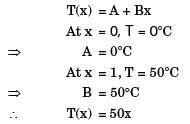
Here,
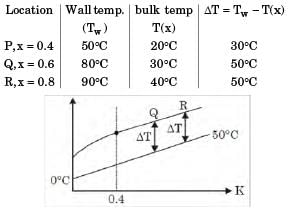
So, Q and R in thermally developed region.
Report a problem
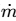 −1
−1 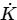 −1 and 2600 J
−1 and 2600 J 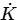 g−1
g−1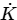 − 1, respectively. The correlation Nu = 0.023 Re 0.8 Pr 0.4 is applicable, where the Nusselt Number (Nu) is defined on the basis of the pipe diameter. The pipe surface temperature at the exit is ________ °C (round off to the nearest integer). [GATE ME 2022, SET-2]
− 1, respectively. The correlation Nu = 0.023 Re 0.8 Pr 0.4 is applicable, where the Nusselt Number (Nu) is defined on the basis of the pipe diameter. The pipe surface temperature at the exit is ________ °C (round off to the nearest integer). [GATE ME 2022, SET-2]
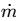 = 1kg/ sec
= 1kg/ sec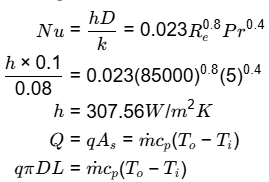

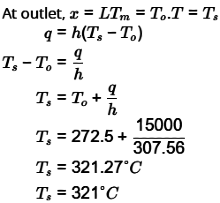
 θ* = (Ts - T) / (Ts - T∞)
θ* = (Ts - T) / (Ts - T∞)


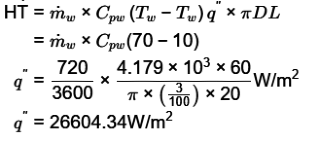 Applying Newton's law of cooling at exit
Applying Newton's law of cooling at exit