Practice Doc: CAT 2020 For Quant (Slot - 2) | Additional Study Material for CAT PDF Download
Q.1. The sum of the perimeters of an equilateral triangle and a rectangle is 90 cm. The area, T, of the triangle and the area, R, of the rectangle, both in sq cm, satisfy the relationship R = T2. If the sides of the rectangle are in the ratio 1: 3, then the length, in cm, of the longer side of the rectangle, is
(a) 24
(b) 27
(c) 21
(d) 18
Ans: b
Solution: Let the breadth of the rectangle be b.
Length of the rectangle = 3b
Let a be the side of the equilateral triangle.
Given,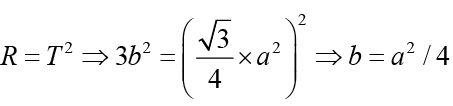
Given,
2(4b) + 3a = 90
⇒ 8 (a2 / 4) + 3a - 90 = 0
⇒ 2a2 + 3a - 90 = 0
⇒ (a - 6)(2a + 15) = 0
⇒ a = 6
∴ b = 9
⇒ 3b = 27
Q.2. In May, John bought the same amount of rice and the same amount of wheat as he had bought in April, but spent ₹ 150 more due to price increase of rice and wheat by 20% and 12%, respectively. If John had spent ₹ 450 on rice in April, then how much did he spend on wheat in May?
(a) ₹ 580
(b) ₹ 570
(c) ₹ 560
(d) ₹ 590
Ans: c
Solution: Amount spent on rice in May = 450 x 1.2 = ? 540.
If the amount spent on wheat in April is w, then in May it would be 1.12w.
Given, (1.12w + 540) - (w + 450) = 150
⇒ 12w = 60
⇒ w = 500
∴ The amount spent on wheat in May =1.12w i.e., ? 560
Q.3. In a car race, car A beats car B by 45 km, car B beats car C by 50 km, and car A beats car C by 90 km. The distance (in km) over which the race has been conducted is
(a) 500
(b) 475
(c) 550
(d) 450
Ans: d
Solution: Let the length of the racetrack be D.
When A covers D km, B covers ( D -45) km and C covers (D-90) km
When B covers D km, C covers ( D -50) km
The ratio of the speeds of the racers is same as the ratio of the distance travelled in a given time period.
Ratio of speed of B and C is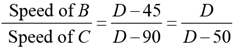
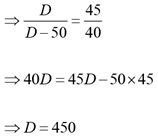
Q.4. John takes twice as much time as Jack to finish a job. Jack and Jim together take one-thirds of the time to finish the job than John takes working alone. Moreover, in order to finish the job, John takes three days more than that taken by three of them working together. In how many days will Jim finish the job working alone?
Ans: 4
Solution: Let the individual times taken by John, Jack and Jim to complete the works be a, b and c respectively.
Given, a = 2b...(1)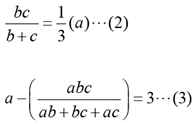
From (1) and (2), we've c = 2b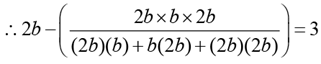
⇒ b = 2
∴ c = 4
Q.5. Let the m-th and n-th terms of a geometric progression be 3/4 and 12 , respectively, where m<n. If the common ratio of the progression is an integer r, then the smallest possible value of r + n - m is
(a) -2
(b) 2
(c) 6
(d) -4
Ans: a
Solution: Tn = 12
Tm = 3 / 4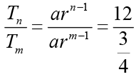
rn- m = 16 = (±2)4 = (±4)2
To get the minimum value for r + n - m, r should be minimum.
∴ r = - 4
n - m = 2
∴ Required answer = -2
Q.6. If x and y are positive real numbers satisfying x + y = 102, then the minimum possible value of 2601 (x + 1/x) (x + 1/y) is
Ans: 2704
Solution: AM ≥ GM ≥ HM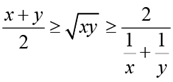
Given x + y = 102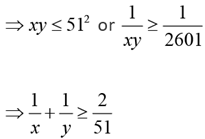
The minimum value of 2601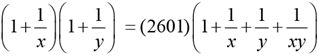
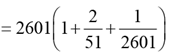
= 2704
Q.7. The value of loga (a/b) + logb (b/a), for 1 < a ≤ b cannot be equal to
(a) -0.5
(b) 1
(c) 0
(d) -1
Ans: b
Solution: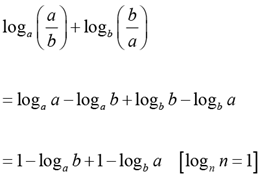
since (logab + logab) ≥ 2
∴ The above value is ≤ 0.
∴ 1 can't be the answer.
Q.8. In how many ways can a pair of integers (x, a) be chosen such that x2 -2|x| + |a - 2| = 0?
(a) 4
(b) 5
(c) 6
(d) 7
Ans: d
Solution: x2-2| x | +|a - 2|= 0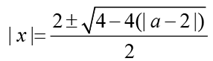
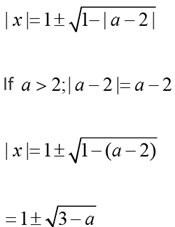
since x is integer 3 - a ≥ 0
a ≤ 3
The possible values of a is = 3
Then x = ± 1;
If a = 2, | x |=| 1 ± 1 |, ⇒ x = ± 2, 0
If a < 2, | a - 2 |= 2 - a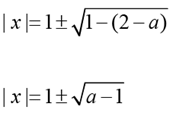
Since x is integer a -1 ≥ 0 ⇒ a ≥ 1
∴ The possible values of a is 1
If a = 1, | x |= 1 ⇒ x = ± 1
∴ The possible pairs =(-1,3), (1,3), (1,1), (-1,1), (2,2),(-2,2), (0,2) i.e., 7
Q.9. Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
1. 20
2. 22
3. 19
4. 21
Ans: a
Solution: Let a, b, c represent number of students who opted for two subjects - Maths and Chemistry, Maths and Physics and Physics and Chemistry respectively.
Given, a + b = 23 - 18 = 5
and b + c = 25 - 18 = 7
Since a, b and c cannot be negative the least value for any of the three is 5 .
We get a + c + 18 = (23 + 25 - 18) - 2b
Minimum value of number of students who chose chemistry = 23 + 25 - 18 - 10 = 20
Q.10. For real x, the maximum possible value of 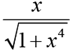 is
is
(a) 1/√3
(b) 1
(c) 1/√2
(d) 1/2
Ans: c
Solution: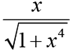
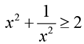
Hence the maximum value of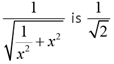
Q.11. Aron bought some pencils and sharpeners. Spending the same amount of money as Aron, Aditya bought twice as many pencils and 10 less sharpeners. If the cost of one sharpener is ₹ 2 more than the cost of a pencil, then the minimum possible number of pencils bought by Aron and Aditya together is
(a) 30
(b) 33
(c) 27
(d) 36
Ans: b
Solution: Let the price of each pencil be Rs. x and price of each sharpens be Rs. y
Aron y - x = 2 ⇒ ∴ x = y - 2
a(y - 2) + b(y) = 2a(y - 2) + (b -10) y
10 y = a(y - 2) → (1)
Required value = 3a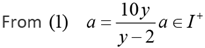
Its possible only when y = 22
∴ a = 11
Required answer = 33
Q.12. A sum of money is split among Amal, Sunil and Mita so that the ratio of the shares of Amal and Sunil is 3 : 2, while the ratio of the shares of Sunil and Mita is 4 : 5. If the difference between the largest and the smallest of these three shares is Rs 400, then Sunil’s share, in rupees, is
Ans: 800
Solution: Given ratio of shares of Amal and Sunil is 3: 2
Also the ratio of shares of Sunil and Mita is 4 : 5.
Hence the ratio of shares of Anil, Sunil and Mita is 6 : 4 : 5
∴ Sunil's share = 400 x 4/2 = 800
Q.13. Anil buys 12 toys and labels each with the same selling price. He sells 8 toys initially at 20% discount on the labeled price. Then he sells the remaining 4 toys at an additional 25% discount on the discounted price. Thus, he gets a total of Rs 2112, and makes a 10% profit. With no discounts, his percentage of profit would have been
(a) 60
(b) 55
(c) 50
(d) 54
Ans: c
Solution: Let the cost price and marked price of each toy be c and m respectively.
Overall selling price = 8(0.8m) + 4(3/4 x 0.8m) i.e 8.8m.
Given, 110% of 12c = 8.8m
⇒ c = 2m/3
∴ Overall CP = 12 x 2m/3 i.e 8m
Required profit percentage = 12m - 8m/8m x 100 = 50%
Q.14. Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2 at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make before he meets Rahim again for the first time is
(a) 4
(b) 3
(c) 2
(d) 5
Ans: b
Solution: Time taken by each of them to complete one round
Time taken for Ram to cover one round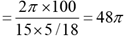
Time taken for Rahim to cover one round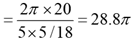
Time taken by Ram and Rahim meet each other for the first time = LCM of 48π and 28.8π = 144π
∴ Number of rounds made by Ram before he meets Rahim for the first time = 144π/48π = 3
Q.15. How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3
Ans: 315
Solution: Consider four blanks
7 is in thousand place, then 3 can be placed in any of the 3 places in 3 ways. Remaining two blanks can be filled with remaining eight digits in 8P2 ways. The number of numbers that have 7 is in thousand place is 3 x 8 P2 = 168
Thousand place cannot be 0,7 and 3, it can be filled with remaining 7 digits in 7 ways. In remaining 3 blanks, 7 and 3 can be arranged in 3 ways. Fourth blank can be filled in 7 ways. The number of numbers that are formed where 7 and 3 is not in thousand place is 7 x 3 x 7 = 147 . Hence total required numbers = 168 + 147 = 315.
Q.16. The number of pairs of integers (x , y) satisfying x ≥ y ≥ -20 and 2x + 5y = 99 is
Ans: 17
Solution: 2x + 5y = 99
When y = - 19, x = 97; since x ≥ y ; the maximum value of y is 13 and corresponding value of x is 17.
We know that the solutions of y are in arithmetic progression with common difference 2.
Here a = - 19, d = 2, tn = 13
tn = a + (n -1)d
-19 + (n - 1)(2) = 13
(n - 1)2 = 32 ⇒ n = 17
Hence number of pairs integers is 17
Q.17. If x and y are non-negative integers such that x + 9 = z, y + 1 = z and x + y < z + 5, then the maximum possible value of 2x + y equals
Ans: 23
Solution: Given x + 9 = z = y + 1 and x + y < z + 5
⇒ (z - 9) + (z -1) < z + 5
⇒ z < 15
Hence the maximum value of z = 14, max of x = 5 and max of y = 13
Required answer, 2x + y = 2 x 5 + 13 = 23
Q.18. A and B are two points on a straight line. Ram runs from A to B while Rahim runs from B to A. After crossing each other, Ram and Rahim reach their destinations in one minute and four minutes, respectively. If they start at the same time, then the ratio of Ram's speed to Rahim's speed is
(a) 2
(b) √2
(c) 2√2
(d) 1/2
Ans: a
Solution: Required ratio of speeds = Square root of inverse ratio of times taken after crossing each other. √4 : √1 i.e., 2 : 1
Q.19. The distance from B to C is thrice that from A to B. Two trains travel from A to C via B. The speed of train 2 is double that of train 1 while traveling from A to B and their speeds are interchanged while traveling from B to C. The ratio of the time taken by train 1 to that taken by train 2 in travelling from A to C is
(a) 1 : 4
(b) 7 : 5
(c) 5 : 7
(d) 4 : 1
Ans: c
Solution: Given,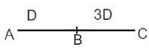
Let the speed of train 1 from A to B be s.
Then the speed of train 2 from A to B is 2s.
Time taken by train 1 to cover A to C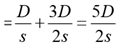
And, time taken by train 2 to cover A to C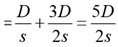
Required ratio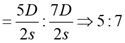
Q.20. Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to
(a) 7.2
(b) 7.8
(c) 6.6
(d) 8.8
Ans: d
Solution: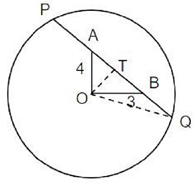
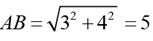
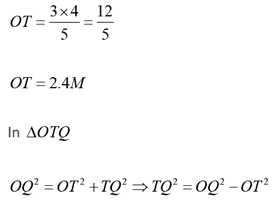
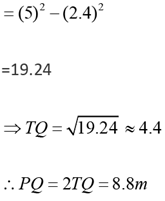
Q.21. The number of integers that satisfy the equality (x2 - 5x + 7) x+1 = 1 is
(a) 2
(b) 3
(c) 5
(d) 4
Ans: b
Solution: (x2 - 5x + 7) x+1= 1
We know, for ab = 1, if
-a = -1 then b is even.
-a = 1 then b is any number
-a > 0 then b = 0
Case 1: x + 1 = 0 ⇒ x = -1
Case 2: x2- 5x + 7 = 1 ⇒ x2 - 5x + 6 = 0 ⇒ x = 2 or 3
Case 3: x2 - 5x + 7 = -1 ⇒ x2 - 5x + 8 = 0
but x is not an integer
∴ The number of integers satisfies the equation is 3
Q.22. Let f (x) = x2 + ax + b and g (x) = f (x + 1) - f (x - 1). If f (x) ≥ 0 for all real x, and g (20) = 72 , then the smallest possible value of b is
(a) 1
(b) 16
(c) 0
(d) 4
Ans: d
Solution: f (x) = x2 + ax + b
g (x) = f (x + 1) - f (x - 1)
= {(x + 1)2 + a(x +1) + b} - {(x -1)2 + a(x -1) + b}
g (x) = 4x + 2a
g (20) = 72
80 + 2a = 72 ⇒ a = - 4
∴ f (x) = x2 - 4x + b
f (x) = (x - 2)2 + b - 4
when b ≥ 4 f (x) ≥ 0 for all x
∴ The minimum value of b is 4
Q.23. Let C1 and C2 be concentric circles such that the diameter of C1 is 2 cm longer than that of C2. If a chord of C1 has length 6 cm and is a tangent to C2, then the diameter, in cm, of C1 is
Ans: 10
Solution: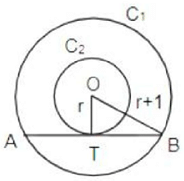
Given, d + 2 = D ⇒ r + 1 = R
In the figure OT = r and OB = r + 1
OT ⊥ AB as AB is the tangent
OT bisects AB i.e., TB = 6/2 =3
Now, in ΔOTB, OT2 + TB2 = OB2
∴ r2 + 32 = (r + 1)2 ⇒ r = 4
∴ D = 2(R) = 2(r + 1) = 10cm
Q.24. From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is
(a) 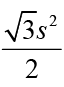
(b) 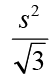
(c) 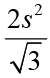
(d) 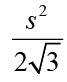
Ans: b
Solution: 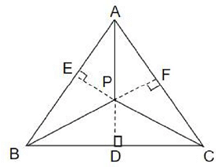
PD + PE + PF = s
Area of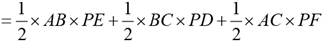
As AB = BC = CA, we've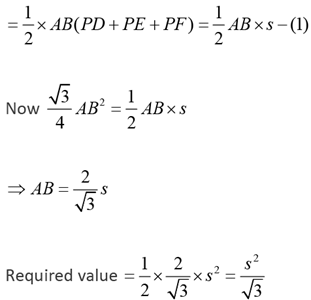
Q.25. For the same principal amount, the compound interest for two years at 5% per annum exceeds the simple interest for three years at 3% per annum by Rs 1125. Then the principal amount in rupees is
Ans: 90000
Solution: Let the principal be P.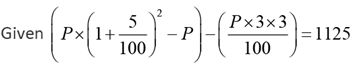
⇒ P(0.1025 - 0.09) = 1125
⇒ P = 90, 000
Q.26. In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by
(a) 4
(b) 3
(c) 5
(d) 6
Ans: a
Solution: Let x1 be the least number
x10 be the largest number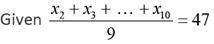
x2 + x3 + ...x9 + x10 = 423 → (1)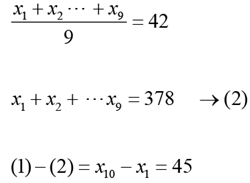
Sum of 10 observations
x1 + x2 + x3 + ...x10 = 423 +x1
Since the minimum value of x10 is 47, the minimum value of x1 is 2, minimum average 423 + 2/10 = 42.5
The maximum value of x1 is 42,
Maximum average
423 + 42/10 = 46.5
Required difference = 4
|
5 videos|385 docs|204 tests
|





















