Practice Doc: CAT 2020 For Quant (Slot - 3) | Additional Study Material for CAT PDF Download
Q.1. If loga30 = A, loga (5/3) = - B and log2a = 1/3, then log3a equals
(a) 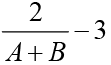
(b) 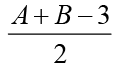
(c) 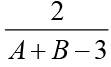
(d) 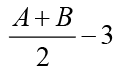
Ans: c
Solution:
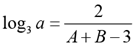
Q.2. Dick is thrice as old as Tom and Harry is twice as old as Dick. If Dick's age is 1 year less than the average age of all three, then Harry's age, in years, is
Ans: 18
Solution: Let the age of Tom be t.
Ages of Dick and Harry are 3t and 6t respectively.
Given,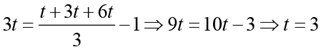
Age of Harry = 6 x 3 = 18
Q.3. A and B are two railway stations 90 km apart. A train leaves A at 9:00 am, heading towards B at a speed of 40 km/hr. Another train leaves B at 10:30 am, heading towards A at a speed of 20 km/hr. The trains meet each other at
(a) 11 : 45 am
(b) 10 : 45 am
(c) 11 : 20 am
(d) 11 : 00 am
Ans: d
Solution: The distance travelled by A before B starts his journey = 40 x 1.5 = 60
The time taken by them to meet each other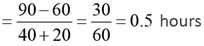
Required answer =10: 30 a.m. +30 min =11: 00 a.m.
Q.4. Let k be a constant. The equations kx + y = 3 and 4x + ky = 4 have a unique solution if and only if
(a) |k| ≠ 2
(b) |k| = 2
(c) k ≠ 2
(d) k = 2
Ans: a
Solution: Simultaneous equation have a unique solution only if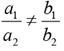
From the given equations, a unique solution would exist only if
k/2 ≠ 2/k
⇒ k2 ≠ 4 ⇒ |k| ≠ 2
Q.5. If x1 = -1 and xm = xm +1 + (m + 1) for every positive integer $m,$ then x100 equals
(a) -5151
(b) -5150
(c) -5051
(d) -5050
Ans: d
Solution: xm + 1 = xm - (m + 1)
x2 = x1 - 2 = -1 - 2 = - 3
x3 = x2 - 3 = -1 - 2 - 3 = - 6
Similarly,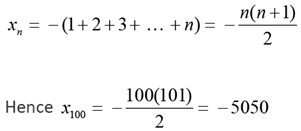
Q.6. Vimla starts for office every day at 9 am and reaches exactly on time if she drives at her usual speed of 40 km/hr. She is late by 6 minutes if she drives at 35 km/hr. One day, she covers two-thirds of her distance to office in one-thirds of her usual time to reach office, and then stops for 8 minutes. The speed, in km/hr, at which she should drive the remaining distance to reach office exactly on time is
(a) 29
(b) 27
(c) 28
(d) 26
Ans: c
Solution: Let the original time taken by Vimla be t minutes 40t / 60 = 35 x (t + 6) / 60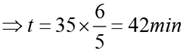
The distance to office = 28 km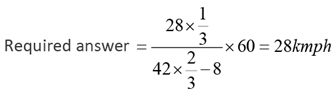
Q.7. A man buys 35 kg of sugar and sets a marked price in order to make a 20% profit. He sells 5 kg at this price, and 15 kg at a 10% discount. Accidentally, 3 kg of sugar is wasted. He sells the remaining sugar by raising the marked price by p percent so as to make an overall profit of 15%. Then p is nearest to
(a) 31
(b) 22
(c) 35
(d) 25
Ans: d
Solution: Let the CP and MP of each kg of sugar be 10x and 12x respectively.
Total cost price = 35 x 10x = 350x
Total selling price = 35 x 10x x 1.15 = 402.5x
Selling price already realized = 5 x 12x + 15 x 12x x 0.9 + 3 x 0 + 12 x 12x x (1 + p/100) = 402.5x
60 + 162 + 0 + 144(1 + p/100) = 402.5
p = 25.34% ≈ 25%
Q.8. If f (x + y) = f (x) f (y) and f (5) = 4, then f (10) - f (-10) is equal to
(a) 0
(b) 15.9375
(c) 3
(d) 14.0625
Ans: b
Solution: Given f (x + y) = f (x) f (y)
⇒ f (x) = ax (where a is a constant) Given, f (5) = 4 ⇒ a5 = 4 ⇒ a = 22/5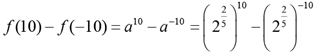
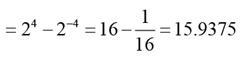
Q.9. If a, b, c are non-zero and 14a = 36b = 84c, then 6b(1/c - 1/a) is equal to
Ans: 3
Solution: Let 14a = 36b = 84c = k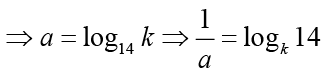
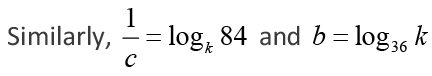
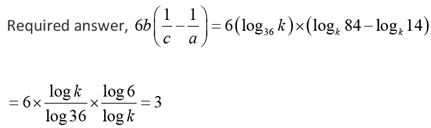
Q.10. A contractor agreed to construct a 6 km road in 200 days. He employed 140 persons for the work. After 60 days, he realized that only 1.5 km road has been completed. How many additional people would he need to employ in order to finish the work exactly on time?
Ans: 40
Solution: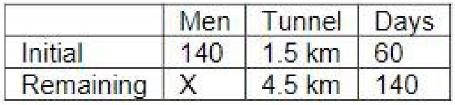
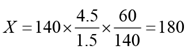
Additional men required = 180 - 140 = 40
Q.11. Let m and n be positive integers, If x2 + mx + 2n = 0 and x2 + 2nx + m = 0 have real roots, then the smallest possible value of m + n is
(a) 7
(b) 8
(c) 5
(d) 6
Ans: d
Solution: Since the roots are real m2 - 8n ≥ 0 and (2n)2 - 4m ≥ 0 ⇒ n2 - m ≥ 0
⇒ n4 ≥ m2 ≥ 8n
⇒ n ≥ 2 and m ≥ 4
Hence the least value of m + n = 2 + 4 = 6
Q.12. A person invested a certain amount of money at 10% annual interest, compounded half-yearly. After one and a half years, the interest and principal together became Rs 18522. The amount, in rupees, that the person had invested is
Ans: 16000
Solution: Let the sum be P. 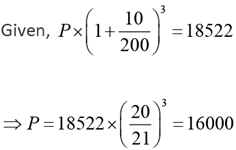
Q.13. Anil, Sunil, and Ravi run along a circular path of length 3 km, starting from the same point at the same time, and going in the clockwise direction. If they run at speeds of 15 km/hr, 10 km/hr, and 8 km/hr, respectively, how much distance in km will Ravi have run when Anil and Sunil meet again for the first time at the starting point?
(a) 4.2
(b) 5.2
(c) 4.8
(d) 4.6
Ans: c
Solution: Time taken by Anil and Sunil meet at the starting point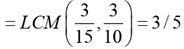
Distance run by Ravi in 3 / 5 hours = (3 / 5) x 8 = 24 / 5 = 4.8 km
Q.14. The area, in sq. units, enclosed by the lines x = 2, y = |x - 2 | +4 , the X -axis and the Y -axis is equal to
(a) 8
(b) 12
(c) 10
(d) 6
Ans: c
Solution: The line y =| x - 2 | +4 intersects the y -axis at (0, 6) and intersects x = 2 at (2, 4)
The other vertices are (0, 0) and (2, 0)
The figure formed is a trapezium of parallel sides 6 and 4 and the distance between the parallel sides is 2.
Required answer = 1/2 x 2 x (6 4) = 10
Q.15. The vertices of a triangle are (0, 0),(4, 0) and (3, 9). The area of the circle passing through these three points is
(a) 14π/3
(b) 12π/5
(c) 123π/7
(d) 205π/9
Ans: d
Solution: a = 4, b = √90 ; c = √82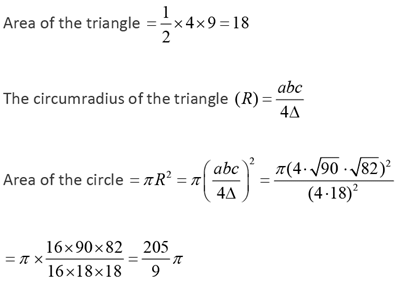
Q.16. How many integers in the set {100, 101, 102, ..., 999} have at least one digit repeated?
Ans: 252
Solution: The given set is a set of all three-digit numbers and the number of numbers in the set = 900.
The number of three-digit numbers having no digits repeating = 9 x 9 x 8 = 648
Required answer = 900 - 648 = 252
Q.17. Let N, x and y be positive integers such that N = x + y, 2 < x < 10 and 14 < y < 23. If N > 25, then how many distinct values are possible for N?
Ans: 6
Solution: Given, 2 < x < 10 and 14 < y < 23 ⇒ 17 < ( x + y ) < 32 i.e. 17 < N < 32
But N > 25 hence 25 < N < 32
N can take 6 distinct values.
Q.18. The points (2,1) and (-3, -4) are opposite vertices of a parallelogram. If the other two vertices lie on the line x + 9 y + c = 0 , then c is
(a) 12
(b) 14
(c) 13
(d) 15
Ans: b
Solution: The given line also passes through the point of intersection of the diagonals of the parallelogram, which is the mid-point of (2,1) and (-3, -4) The mid-point of the given two points is (-1/2, -3/2).
Substituting the point in the given equation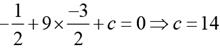
Q.19. How many pairs (a, b) of positive integers are there such that a ≤ b and ab = 42017?
(a) 2017
(b) 2019
(c) 2020
(d) 2018
Ans: d
Solution: Given, a × b = 42017 = 24034
Since a × b = 42017, is a perfect square the number of factors of 24034 is odd.
Required answer, the number of values of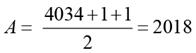
Q.20. In a trapezium ABCD, AB is parallel to DC, BC is perpendicular to DC and ∠BAD = 45°. If DC = 5 cm, BC = 4 cm, the area of the trapezium in sq cm is
Ans: 28
Solution: Dropping a perpendicular DE onto AB, the figure is divided into two parts - a rectangle of dimensions 4 × 5 and an isosceles triangle AED.
Required answer = Area of rectangle + Area of triangle = 4 × 5 + 1/2(4 × 4) = 28cm2
Q.21. How many of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7?
(a) 40
(b) 42
(c) 43
(d) 41
Ans: d
Solution: The required answer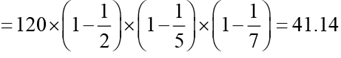
Required answer is the integral part of 41.14 = 41
Q.22. Two alcohol solutions, A and B, are mixed in the proportion 1:3 by volume. The volume of the mixture is then doubled by adding solution A such that the resulting mixture has 72% alcohol. If solution A has 60% alcohol, then the percentage of alcohol in solution B is
(a) 94%
(b) 92%
(c) 90%
(d) 89%
Ans: b
Solution: Let the quantity of solutions A and B mixed initially be p and 3p respectively.
After an additional 4p of solution A is added 60% of (1 p + 4 p) + x% of 3 p = 72% of (1p + 4p + 3p) ⇒ x = 92
Q.23. 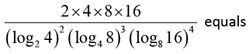
Ans: 24
Solution: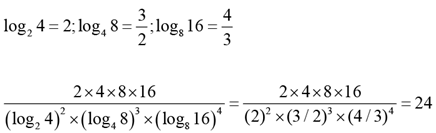
Q.24. A batsman played n + 2 innings and got out on all occasions. His average score in these n + 2 innings was 29 runs and he scored 38 and 15 runs in the last two innings. The batsman scored less than 38 runs in each of the first n innings. In these n innings, his average score was 30 runs and lowest score was x runs. The smallest possible value of x is
(a) 2
(b) 3
(c) 4
(d) 1
Ans: a
Solution: Total score in (n + 2) innings = 29 x (n + 2)
The total score in n innings = 29(n + 2) - 38 - 15
= 29n + 5 = 30n ⇒ n = 5
Total score in 5 innings = 30 x 5 = 150 = 37 x 4 + 2
Q.25. In the final examination, Bishnu scored 52% and Asha scored 64%. The marks obtained by Bishnu is 23 less, and that by Asha is 34 more than the marks obtained by Ramesh. The marks obtained by Geeta, who scored 84%, is
(a) 439
(b) 399
(c) 357
(d) 417
Ans: b
Solution: Let the total marks be T and scores of Bishnu, Asha and Ramesh be a, b and c respectively.
Given, a = 52% of T = c - 23 and b = 64% of T = c + 34
Hence, (64 - 52)% of T = (c + 34) - (c - 23) = 57
i.e. 12% of T = 57
Hence, score of Geeta = 84% of T = 7 x 57 = 399
Q.26. Let m and n be natural numbers such that n is even and 0.2 < m/20, n/m, n/11 < 0.5. Then m - 2n equals
(a) 3
(b) 4
(c) 1
(d) 2
Ans: c
Solution: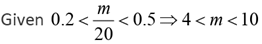
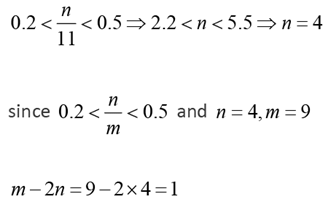
|
5 videos|385 docs|204 tests
|















