Trigonometric Ratios & Identities- 1 | Mathematics (Maths) for JEE Main & Advanced PDF Download
Introduction to Trigonometry
- The word 'trigonometry' is derived from the Greek words 'trigon' and 'metron' and it means 'measuring the sides of a triangle'. The subject was originally developed to solve geometric problems involving triangles. It was studied by sea captains for navigation, surveyor to map out the new lands, by engineers and others.
- Currently, trigonometry is used in many areas such as the science of seismology, designing electric circuits, describing the state of an atom, predicting the heights of tides in the ocean, analysing a musical tone and in many other areas.
Measurement of Angles
There are two systems of measurement of angles:
(i) Sexagesimal or English System: Here 1 right angle = 90 (degrees)
1 = 60’ (minutes)
1’ = 60" (seconds)
(ii) Circular System: Here an angle is measured in radians. One radian corresponds to the angle subtended by an arc of length ’r ’ at the centre of the circle of radius r. It is a constant quantity and does not depend upon the radius of the circle.
(a) Relation between the two systems: Degree = Radian*180 / π
(b) If θ is the angle subtended at the centre of a circle of radius 'r',
by an arc of length 'l' then l / r = θ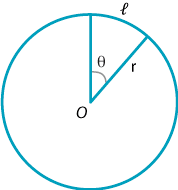
Note: l, r are in the same units and θ is always in radians.
Example.1. If the arcs of the same length in two circles subtend angles of 60° and 75° at their centres. Find the ratio of their radii.
Solution. Let r1 and r2 be the radii of the given circles and let their arcs of the same length s subtend angles of 60 and 75 at their centres.
Now,
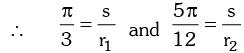
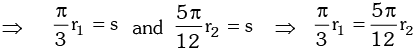
⇒ 4r1 = 5r2 ⇒ r1 : r2 = 5 : 4
T-ratios (or Trigonometric Functions)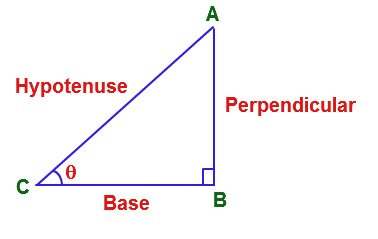
In a right angle triangle sin θ = p / h, cos θ = b / h, tan θ = p / b, cosec θ = h / p, sec θ = h / b and cot θ = b / p
'p' is perpendicular, 'b' is base and 'h' is hypotenuse.
Note : The quantity by which the cosine falls short of unity i.e. 1 - cosθ, is called the versed sine θ of θ and also by which the sine falls short of unity i.e. 1- sinθ is called the coversed sine of θ.
➢ New Definition of T-ratios 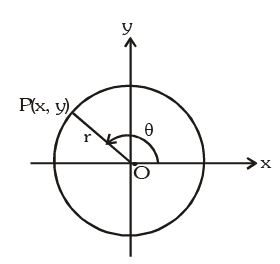 By using rectangular coordinates the definitions of trigonometric functions can be extended to angles of any size in the following way (see diagram). A point P is taken with coordinates (x, y). The radius vector OP has length r and the angle 0 is taken as the directed angle measured anticlockwise from the x-axis.
By using rectangular coordinates the definitions of trigonometric functions can be extended to angles of any size in the following way (see diagram). A point P is taken with coordinates (x, y). The radius vector OP has length r and the angle 0 is taken as the directed angle measured anticlockwise from the x-axis.
The three main trigonometric functions are then defined in terms of r and the coordinates x and y:
- sinθ = y / r
- cosθ = x / r
- tanθ = y / x
(The other function are reciprocals of these)
This can give negative values of the trigonometric functions.
Basic Trigonometric Identities
(i) sin θ. cosec θ = 1
(ii) cos θ. sec θ = 1
(iii) tan θ. cot θ = 1
(iv) tan θ = sin θ / cos θ & cot θ = cos θ / sin θ
(v) sin2 θ + cos2 θ = 1 or sin2 θ = 1 - cos2 θ or cos2 θ = 1 - sin2 θ
(vi) sec2 θ - tan2 θ = 1 or sec2 θ = 1 + tan2 θ or tan2 θ = sec2 θ - 1
(vii) 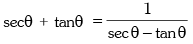
(viii) cosec2 θ - cot2 θ = 1 or cosec2 θ = 1 + cot2 θ or cot2 θ = cosec2 θ - 1
(ix) 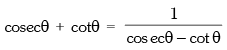
(x) Expressing trigonometrical ratio in terms of each other:
Example.2. If sin θ + sin2 θ = 1 , then prove that cos12 θ + 3 cos10 θ + 3 cos8 θ + cos6 θ - 1 = 0
Solution. Given that sin θ = 1 - sin2 θ = cos2 θ
L.H.S. = cos6 θ (cos2 θ + 1)3 - 1= sin3 θ (1 + sin θ )3 - 1= (sin θ + sin2 θ)3 - 1 = 1 - 1 = 0
Example.3. 2(sin6 θ + cos6 θ) - 3 ( sin4 θ + cos4 θ) + 1 is equal to
(a) 0
(b) 1
(c) –2
(d) none of these
Ans. (a)
Solution. 2 [(sin2 θ + cos2 θ )3 - 3 sin2 θ cos2 θ ( sin2 θ + cos2 θ) ] - 3 [(sin2 θ + cos2 θ)]2 - 2sin2 θ cos2 θ] + 1
= 2 [1 – 3 sin2 θ cos2 θ] - 3 [1 - 2 sin2 θ cos2 θ] + 1
= 2 - 6 sin2 θ cos2 θ - 3 + 6 sin2 θ cos2 θ + 1 = 0
Signs of Trigonometric Functions in Different Quadrants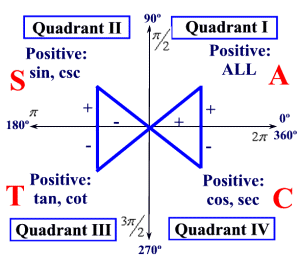

Trigonometric Functions of Allied Angles
(a) sin (2n π + θ) = sin θ, cos (2n π + θ) = cos θ, where n ∈ I
(b)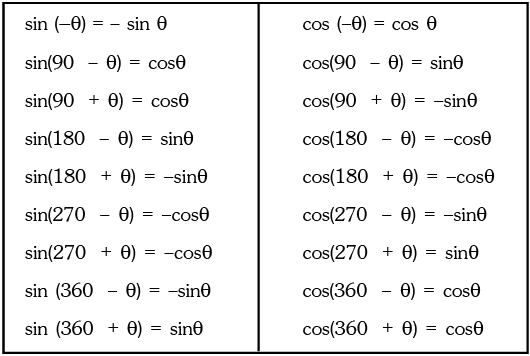
Values of T-ratios of Some Standard Angles
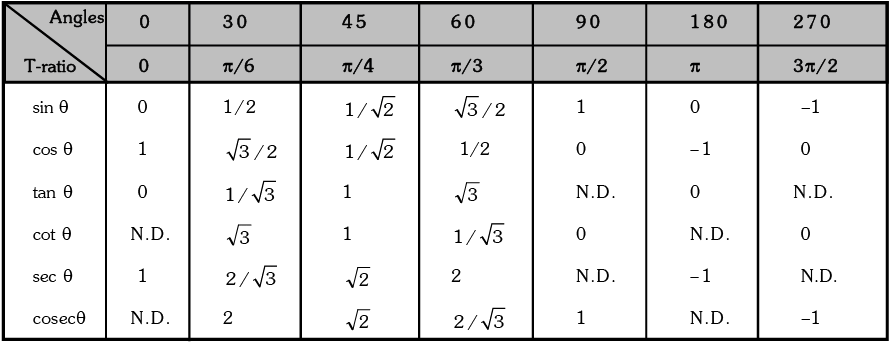
N.D. → Not Defined
(a) sin nπ = 0 ; cos nπ = (-1)n; tan nπ = 0 where n ∈ I
(b) sin(2n + 1) π / 2 = (-1)n; cos(2n + 1) π / 2 = 0 where n ∈ I
Example.4. If sin θ = -1 / 2 and tan θ = 1 / √3 then θ is equal to:
(a) 30°
(b) 150°
(c) 210°
(d) None of these
Ans. (c)
Solution. Let us first find out θ lying between 0 and 360°.
Since sin θ = -1 / 2 ⇒ θ = 210° or 330° and tan θ = 1 / √3 ⇒ θ = 30° or 210°
Hence, θ = 210° or 7π / 6 is the value satisfying both.
Graph of Trigonometric Functions
(i) y = sinx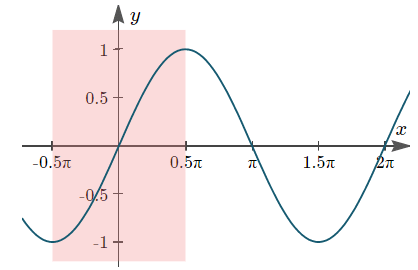
(ii) y = cosx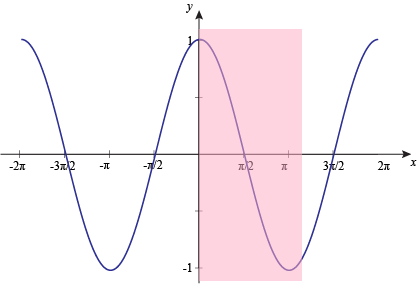
(iii) y = tanx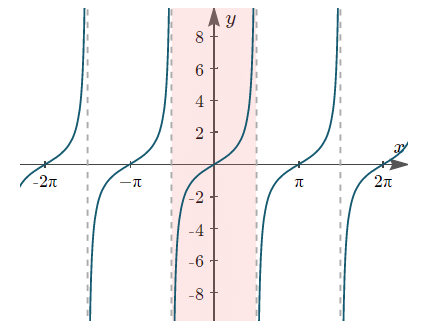 (iv) y = cotx
(iv) y = cotx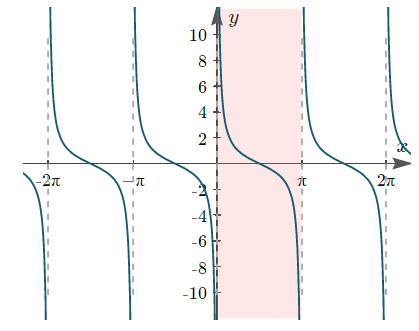 (v) y = secx
(v) y = secx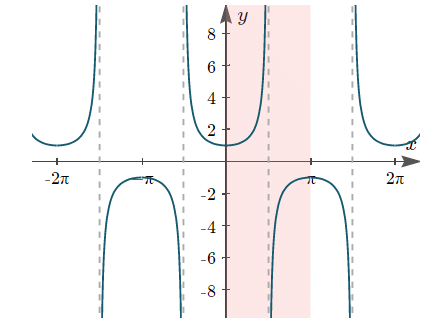
(vi) y = cosecx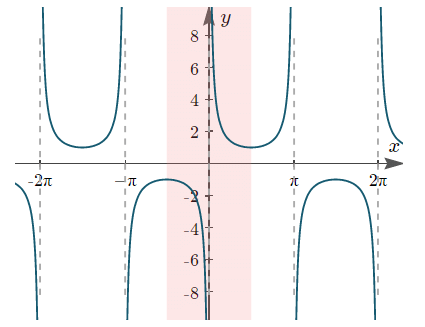
Domains, Ranges and Periodicity of Trigonometric Functions
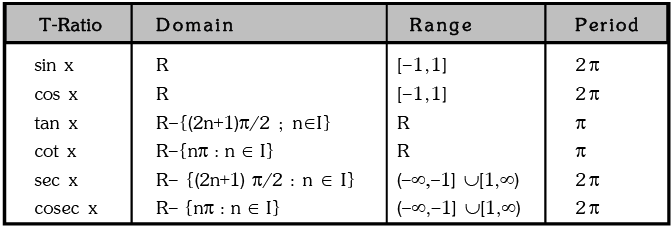
|
172 videos|476 docs|154 tests
|
FAQs on Trigonometric Ratios & Identities- 1 - Mathematics (Maths) for JEE Main & Advanced
| 1. What are T-ratios and how are they related to trigonometric functions? |  |
| 2. What are the basic trigonometric identities? |  |
| 3. How do the signs of trigonometric functions vary in different quadrants? |  |
| 4. What are allied angles and how are they related to trigonometric functions? |  |
| 5. What are the domains, ranges, and periodicity of trigonometric functions? |  |





















