JEE Exam > JEE Notes > Additional Study Material for JEE > Electric Potential of Uniformly Charged Ring, Rod, and Disc
Electric Potential of Uniformly Charged Ring, Rod, and Disc | Additional Study Material for JEE PDF Download
Electric Potential Due to a Charged Ring
Let electric potential at point P due to small element of length dℓ be dV.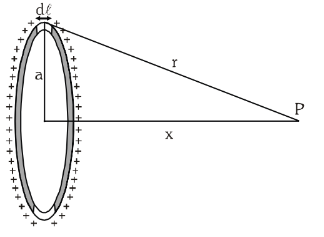
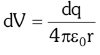
(distance between small element and point P is equal to r)
Electric potential due to whole ring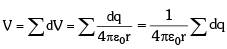
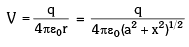
Potential Due to a Uniformly Charged Rod
Electric Potential due to a uniformly charged rod of length L and linear charge density lambda, at a point P on its axial line which is d units away from it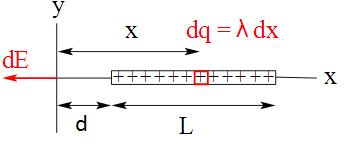
Charge per unit length λ = Q/L
Charge of slice dq = λ.dx
Electric potential: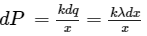 
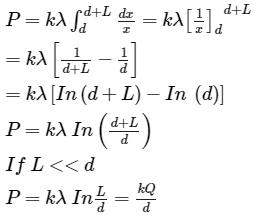
Potential Due to a Uniformly Charged Disc
Find the electric potential at the axis of a uniformly charged disc and use potential to find the electric field at same point.
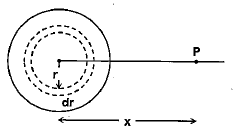
Potential due to ring element of radius r and thickness dr is dv:
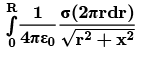
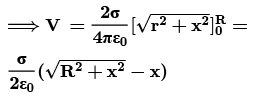
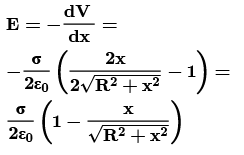
The document Electric Potential of Uniformly Charged Ring, Rod, and Disc | Additional Study Material for JEE is a part of the JEE Course Additional Study Material for JEE.
All you need of JEE at this link: JEE
|
22 videos|162 docs|17 tests
|
FAQs on Electric Potential of Uniformly Charged Ring, Rod, and Disc - Additional Study Material for JEE
| 1. What is the electric potential of a uniformly charged ring? |  |
Ans. The electric potential of a uniformly charged ring at a point on its axis is given by the equation V = kQ/(√(R^2 + x^2)), where V is the electric potential, k is the electrostatic constant, Q is the charge of the ring, R is the radius of the ring, and x is the distance from the center of the ring to the point on its axis.
| 2. How is the electric potential of a uniformly charged rod calculated? | |
Ans. The electric potential of a uniformly charged rod at a point on its perpendicular bisector is given by the equation V = (kλ/2πε) * ln((R + √(R^2 + d^2))/(R - √(R^2 + d^2))), where V is the electric potential, k is the electrostatic constant, λ is the linear charge density of the rod, ε is the permittivity of free space, R is the length of the rod, and d is the distance from the center of the rod to the point on its perpendicular bisector.
| 3. What is the electric potential of a uniformly charged disc at its center? | |
Ans. The electric potential of a uniformly charged disc at its center is given by the equation V = (kσ/2ε) * (1 - √(2)), where V is the electric potential, k is the electrostatic constant, σ is the surface charge density of the disc, and ε is the permittivity of free space.
| 4. How does the electric potential of a uniformly charged ring vary along its axis? | |
Ans. The electric potential of a uniformly charged ring decreases as the distance from the center of the ring to the point on its axis increases. It follows an inverse square law, where the electric potential is inversely proportional to the square root of the sum of the square of the distance and the square of the ring's radius.
| 5. What happens to the electric potential of a uniformly charged rod as the distance from its center increases? | |
Ans. The electric potential of a uniformly charged rod decreases as the distance from its center increases. It follows a logarithmic relationship, where the electric potential decreases as the natural logarithm of the ratio of the sum of the length of the rod and the distance from its center to the difference of the length of the rod and the distance from its center.
Related Exams
About this Document
|
4.90/5 Rating |
|
Dec 22, 2024 Last updated |
Document Description: Electric Potential of Uniformly Charged Ring, Rod, and Disc for JEE 2024 is part of Additional Study Material for JEE preparation.
The notes and questions for Electric Potential of Uniformly Charged Ring, Rod, and Disc have been prepared according to the JEE exam syllabus. Information about Electric Potential of Uniformly Charged Ring, Rod, and Disc covers topics
like and Electric Potential of Uniformly Charged Ring, Rod, and Disc Example, for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Electric Potential of Uniformly Charged Ring, Rod, and Disc.
Introduction of Electric Potential of Uniformly Charged Ring, Rod, and Disc in English is available as part of our Additional Study Material for JEE
for JEE & Electric Potential of Uniformly Charged Ring, Rod, and Disc in Hindi for Additional Study Material for JEE course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: Electric Potential of Uniformly Charged Ring, Rod, and Disc | Additional Study Material for JEE
Description
Full syllabus notes, lecture & questions for Electric Potential of Uniformly Charged Ring, Rod, and Disc | Additional Study Material for JEE - JEE | Plus excerises question with solution to help you revise complete syllabus for Additional Study Material for JEE | Best notes, free PDF download
Information about Electric Potential of Uniformly Charged Ring, Rod, and Disc
In this doc you can find the meaning of Electric Potential of Uniformly Charged Ring, Rod, and Disc defined & explained in the simplest way possible. Besides explaining types of
Electric Potential of Uniformly Charged Ring, Rod, and Disc theory, EduRev gives you an ample number of questions to practice Electric Potential of Uniformly Charged Ring, Rod, and Disc tests, examples and also practice JEE
tests
|
Explore Courses for JEE exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
study material
,mock tests for examination
,Rod
,and Disc | Additional Study Material for JEE
,practice quizzes
,Rod
,Semester Notes
,Objective type Questions
,Previous Year Questions with Solutions
,Electric Potential of Uniformly Charged Ring
,past year papers
,and Disc | Additional Study Material for JEE
,Viva Questions
,shortcuts and tricks
,Exam
,Important questions
,and Disc | Additional Study Material for JEE
,Electric Potential of Uniformly Charged Ring
,Electric Potential of Uniformly Charged Ring
,Rod
,Extra Questions
,Sample Paper
,Free
,video lectures
,MCQs
,Summary
,ppt
;
Additional Information about Electric Potential of Uniformly Charged Ring, Rod, and Disc for JEE Preparation
Electric Potential of Uniformly Charged Ring, Rod, and Disc Free PDF Download
The Electric Potential of Uniformly Charged Ring, Rod, and Disc is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Electric Potential of Uniformly Charged Ring, Rod, and Disc now and kickstart your journey towards success in the JEE exam.
Importance of Electric Potential of Uniformly Charged Ring, Rod, and Disc
The importance of Electric Potential of Uniformly Charged Ring, Rod, and Disc cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Electric Potential of Uniformly Charged Ring, Rod, and Disc Notes
Electric Potential of Uniformly Charged Ring, Rod, and Disc Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Electric Potential of Uniformly Charged Ring, Rod, and Disc.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Electric Potential of Uniformly Charged Ring, Rod, and Disc Notes on EduRev are your ultimate resource for success.
Electric Potential of Uniformly Charged Ring, Rod, and Disc JEE Questions
The "Electric Potential of Uniformly Charged Ring, Rod, and Disc JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Electric Potential of Uniformly Charged Ring, Rod, and Disc on the App
Students of JEE can study Electric Potential of Uniformly Charged Ring, Rod, and Disc alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Electric Potential of Uniformly Charged Ring, Rod, and Disc,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Electric Potential of Uniformly Charged Ring, Rod, and Disc is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup