Sample Question Paper- 1 | Mathematics (Maths) Class 8 PDF Download
Class - VIII
Mathematics
Time - 3 hrs
M.M. - 80 Marks
General Instructions :
1. All questions are compulsory.
2. The question paper consist of 30 questions divided into four sections A, B, C and D. Section A comprises of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of 3 marks each and Section D comprises of 8 questions of 4 marks each.
3. There is no overall choice. 4. Use of calculator is not allowed.
SECTION ‘A’ (1 mark each)
Q.1. Find the perfect square numbers between : 30 and 40
Ans. The perfect square numbers between 30 and 40 is 36.
Q.2. Multiply the following :
(a) 15xy2, 17yz2
(b) – 5a2bc, 11ab, 13abc2
Ans. (a) 15xy2 × 17yz2 = (15 × 17) × x × y2 × y × z2
= 255 xy3z2
(b) – 5a2bc × 11ab × 13abc2 = (– 5 × 11 × 13) a2bc × ab × abc2
= – 715 a4b3c3
Q.3. Express 16–2 as a power with the base 2.
Ans.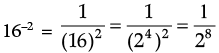
= 2–8
Q.4. A polyhedron is having 8 vertices and 12 edges. How many faces of it are there ?
Ans.
Number of vertices (V) = 8
Number of edges (E) = 12.
Let the number of faces be F
Now, using Euler’s formula
F + V = E + 2
We have,
F + 8 = 12 + 2
⇒ F + 8 = 14
⇒ F = 14 – 8
⇒ F = 6.
Thus, the required number of faces = 6
Q.5. Write 0.000005678 in the standard form.
Ans.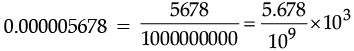
= 5.678 × 10–6
Q.6. What is a parallelepiped ?
Ans. When the ends of a quadrilateral prism are parallelograms, then it is called a parallelepiped.
SECTION ‘B’ (2 marks each)
Q.7. 160 m3 of water is to be used to irrigate a rectangular field whose area is 800 m2. What will be the height of the water level in the field ?
Ans.
Volume of water = 160 m3
Area of rectangular field = 800 m2
Let h be the height of water level in the field.
Now, volume of water = volume of cuboid formed on the field by water.
160 = Area of base × height
= 800 × h
So, required height = 0.2 m.
Q.8. If 16 shirts of equal size can be made out of 24 m of cloth, how much cloth is needed for making one shirt ?
Ans. Cloth needed of 16 shirt = 24 m
Cloth needed for 1 shirt =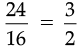
= 1.5 m
Q.9. 72% of 25 students are good in Mathematics. How many are not good in Mathematics ?
Ans. Given, 72% of 25 students are good in Mathematics, then real value of students are good in Mathematics
= 72% of 25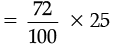
= 18 students are good in Mathematics
Students who are not good in Mathematics = Total students – Students good in Mathematics
= 25 – 18
= 7
Q.10. Factorise the following :
(a) 18 + 11x + x2
(b) y2 – 2y – 15
Ans. (a) 18 + 11x + x2 = x2 + 11x + 18
= x2 + (9 + 2) x + 18
= x2 + 9x + 2x + 18
= x (x + 9) + 2 (x + 9)
= (x + 9) (x + 2)
(b) y2 – 2y – 15
= y2 – (5 – 3) y – 15
= y2 – 5y + 3y – 15
= y(y – 5) + 3(y – 5)
= (y – 5) (y + 3)
Q.11. A colour T.V. is available for Rs. 26880 inclusive of VAT. If the original cost of the T.V. is Rs. 24,000, find the rate of VAT.
Ans. Let the rate of VAT = x%
Then 24000 + x% of 24000 = 26880
or 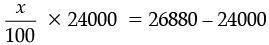
or 240x = 2880
or 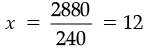
Therefore, Rate of VAT = 12%
Q.12. Simplify : 3x (4x – 5) + 3 and find its value
(a) x = 3
(b) x = 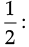
Ans.
3x (4x – 5) + 3
= 3x (4x – 5) + 3
= 12x2 – 15x + 3
(a) For x = 3,
= 12 (3)2 – 15(3) + 3
= 12 (9) – 45 + 3
= 108 – 45 + 3 = 66
(b) For x = 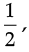
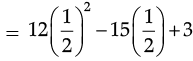
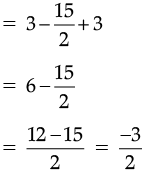
SECTION ‘C’ (3 marks each)
Q.13. The sum of two rational numbers is  if one of them is
if one of them is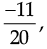 find the other.
find the other.
Ans. ∵ (a rational number) =
(a rational number) = 
∴ The required rational number = 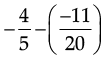
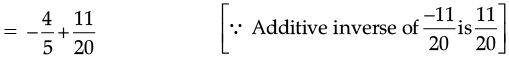
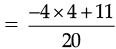 [∵ LCM of 5 and 20 is 20]
[∵ LCM of 5 and 20 is 20]
Thus, the other rational number = 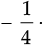
Q.14. If 25 metres of costs Rs. 337.50, then
(a) What will be the cost of 40 metres of the same type of cloth ?
(b) What will be the length of the cloth bought for Rs. 810 ?
Ans.
(a) Let cost of cloth be Rs. x.
Here, cost will be increase by increasing the length of cloth. Hence, it is directly proportional.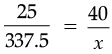
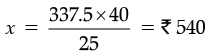
Q.15. A volleyball court is in a rectangular shape and its dimensions are directly proportional to the dimensions of the swimming pool given below. Find the width of the pool.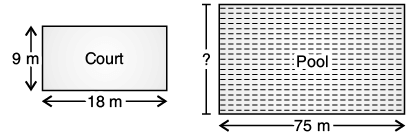 Ans. Here, a volleyball court and a swimming pool both are in rectangular shape and their dimensions are directly proportional. Let l and b are length and breadth, respectively.
Ans. Here, a volleyball court and a swimming pool both are in rectangular shape and their dimensions are directly proportional. Let l and b are length and breadth, respectively.
If l = b
⇒ 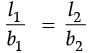
Here, l1 = 18 m, b1 = 9 m, l2 = 75 m, b2 = ?
Then, 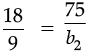
2b2 = 75
b2 =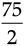
b2 = 37.5 m
So, the width of the pool is 37.5 m.
Q.16. Simplify :
Ans.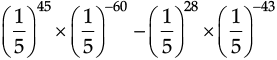

Q.17. During a sale, a shop offered a discount of 10% on the market price of all the items. What would a customer have to pay for a pair of jeans market at Rs. 1450 and two shirts marked at Rs. 850 each.
Ans. The market price of jeans = Rs. 1450
Discount % = 10%
Discount value = 
S.P after 10% discount = 1450 – 145 = Rs.1305
The market price of 2 shirts = 2 × 850 = Rs. 1700
Discount on two shirts = 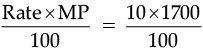
= Rs. 170
∴ S. P. of two shirts = Rs. 1700 – Rs. 170 = Rs. 1530
∴ The customer had to pay = Rs. 1305 + Rs. 1530
= Rs. 2835
Q.18. Radius of a cylinder is r and the height is h. Find the change in the volume if the
(a) height is doubled
(b) height is doubled and the radius is halved
(c) height remains same and the radius is halved.
Ans.
Volume of cylinder = πr2h
(a) Height is doubled i.e., h’ = 2h
Volume of cylinder = πr2h’
= πr2 (2h)
= 2πr2h (Double of the original)
(b) h’ = 2h and r’ = r/2
Then volume of cylinder = πr2h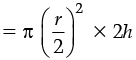
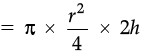
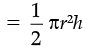 (Half of the original)
(Half of the original)
(c) 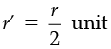
Volume of cylinder = pπr’2h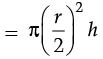
 (One fourth of the original)
(One fourth of the original)
Q.19. Find the area to be painted in the following block with a cylindrical hole. Given that length is 15 cm, weight 12 cm, and radius of the hole 2.8 cm.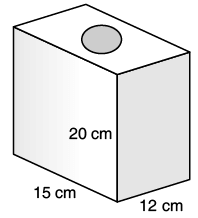
Ans.
Here, l = 15 cm, b = 12 cm, h = 20 cm
and r = 2.8 cm
Surface area of cuboid = 2(lb + bh + hl) = 2(15 × 12 + 12 × 20 + 20 × 15)
= 2(180 + 240 + 300)
= 2 × 720
= 1440 cm2
Area of two holes = 2πr2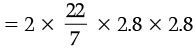
= 49.28 cm2
So, Required area for paint = S.A. of cuboid – area of holes
= 1440 – 49.28
= 1390.72 cm2
Q.20. (a) Find the compound interest on Rs. 31250 at 8% per annum for 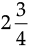 years.
years.
(b) Mohit bought a CD for Rs. 750 and sold it for Rs. 875. Show that his gain percent is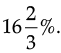
Ans. (a) Since, P = Rs. 31250, n =  years, R = 8% p.a.
years, R = 8% p.a.
Then, A = 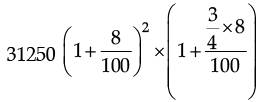

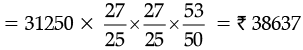
Hence, C.I. = 38637 – 31250 = Rs. 7387
(b) Since, C.P. = Rs. 750 and S.P = Rs. 875
C.P. < S.P.
Gain = Rs. (875 – 750) = Rs. 125
Then, 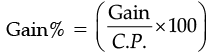
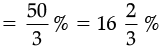
AD = BC = b
CO = AO’ = h
Q.21. Two persons could fit new windows in a house in 3 days.
(a) One of the persons fell ill before the work started. How long would the job take now ?
(b) How many persons would be needed to fit the windows in one day ?
Ans. (a) Let the job take x days
More the persons, the lesser the days. Hence, this is a case of inverse proportion
So, 2 × 3 = 1 × x
⇒ x = 6
Thus, the job would take 6 days.
(b) Let x persons needed to fit the windows in one day
This is case of inverse proportion
∴ 2 × 3 = x × 1
⇒ x = 6
Thus, 6 persons would be needed.
Q.22. If a + b = 25 and a2 + b2 = 225, then find ab.
Ans. We know that, (a + b)2 = a2 + b2 + 2ab
Here, a + b = 25, a2 + b2 = 225
⇒ (25)2 = 225 + 2ab
⇒ 625 = 225 + 2ab
625 – 225 = 2ab
⇒ 400 = 2ab
⇒ 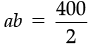
⇒ ab = 200
SECTION ‘D’ (4 marks each)
Q.23. Factorise and divide the following :
(a) (x2 – 22x + 117) / (x – 13)
(b) (9x2 – 4) / (3x + 2)
Ans.
(a) (x2 – 22x + 117) ÷ (x – 13)
∵ x2 – 22x + 117 = x2 – (13 + 9) x + 117
= x2 – 13x – 9x + 117
= x (x – 13) – 9 (x – 13)
= (x – 13) (x – 9)
∴ 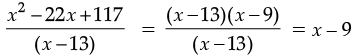
(b) (9x2 – 4) ÷ (3x + 2)
∵ 9x2 – 4 = (3x)2 – (2)2
= (3x + 2) (3x – 2)
∴ 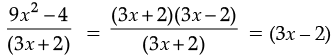
Q.24. Half of a herd of deer are grazing in the field and three fourths of the remaining are playing nearby. The rest 9 are drinking water from the pond. Find the number of deer in the herd.
Ans. Let the total number of deer in the herd be x.
According to question,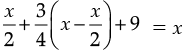
or, 
or,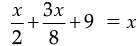
or, 
or, 7x + 72 = 8x
or, 7x – 8x = – 72
or, – x = – 72 or, x = 72
Hence, the required number of deers in the herd are 72.
Q.25. The students of Anju’s class sold posters to raise money. Anju wanted to create a ratio for finding the amount of money her class would make for different numbers of posters sold. She knew they could raise Rs. 250 for every 60 posters sold.
(a) How much money would Anju’s class make for selling 102 posters ?
(b) Could Anju’s class raise exactly Rs. 2,000 ? If so, how many posters would they need to sell ? If not, why ?
Ans. Here, Anju’s class raised money for every 60 posters.
(a) Let x be the money.
Clearly, number of poster will increase, money raised will also increased. This is case of direct proportion
∴ 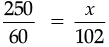
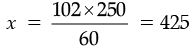
Money raised by 102 poster is Rs. 425.
(b) No, class could not raise exactly Rs. 2000.
Let the number of poster Anju’s class need to sell be n.
∴ 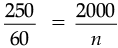

So, required number of posters are 480.
Q.26. (a) Divide 34 into two parts in such a way that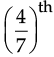 of one part is equal to
of one part is equal to of the other.
of the other.
(b) Which of the following equation are linear equation in one variable.
(a) x2 + x = 1
(b) 2x – 7 = 2/3
(c) x2 + x = 10
(d) x – 15 = 3x
Ans. (a) Let, Ist part = x
Then, IInd part = (34 – x)
According to question,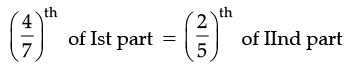
or 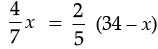
or 20x = 14 (34 – x), [by cross multiplication]
or 20x = 14 × 34 – 14x
or 20x + 14x = 14 × 34
or 34x = 14 × 34
or 
or x = 14
Hence, two parts are 14 and 34 – 14 = 20
i.e., Ist part = 14 and IInd part = 20
(b) Linear equation in one variable are
(c) 2x – 7 = 2/3 and (d) x – 15 = 3x
Q.27. Lakshmi is a cashier in a bank. She has currency notes of denominations Rs. 100, Rs. 50 and Rs. 10 respectively. The ratio of the number of these notes is 2 : 3 : 5. The total cash with Lakshmi is Rs. 400,000. How many notes of each denomination does she have ?
Ans. Let number of notes be 2x, 3x and 5x
According to question,
2x × 100 + 3x × 50 + 5x × 10 = 4,00,000
or 200x + 150x + 50x = 4,00,000
or 400x = 4,00,000
or 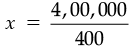
[Dividing both sides by 400]
or x = 1,000
Hence, Number of denomination of Rs. 100 notes
= 2 × 1,000
= 2,000
Number of denomination of Rs. 50 notes = 3 × 1,000= 3,000
= 3,000
Number of denomination of notes Rs. 10 notes
= 5 × 1,000
= 5,000
Hence, required denominations of notes of Rs. 100, Rs. 50 and Rs. 10 are 2,000, 3,000 and 5,000 respectively.
Q.28. Factorise :
(a) a4 – b4
(b) p4 – 81
(c) x4 – (y + z)4
(d) x4 – (x – z)4
Ans.
(a) a4 – b4 = (a2)2 – (b2)2
= (a2 – b2) (a2 + b2)
= (a – b) (a + b) (a2 + b2)
(b) p4 – 81 = (p2)2 – (9)2
= (p2 – 9) (p2 + 9)
= [ (p)2 – (3)2] (p2 + 9)
= (p – 3) (p + 3) (p2 + 9)
(c) x4 – (y + z)4 = (x2)2 – {(y + z)2}2
= {x2 – (y + z)2} {x2 + (y + z)2}
= {x – (y + z)}{x + (y + z)} {x2 + (y +z)2}
= (x – y – z) (x + y + z) {x2 + (y + z)2}
(d) x4 – (x – z)4 = (x2)2 – {(x – z)2]2
= {x2 – (x – z)2} {x2 + (x – z)2}
= (x – x + z) (x + x – z) {x2 + (x – z)2}
Q.29. Find the volume of cuboid whose dimensions are (x2 – 2), (2x + 2) and (x – 1).
Volume of a cuboid = Length × Breadth × Height
Ans.
= (x2 – 2) [(2x + 2)(x – 1)]
= (x2 – 2) [2x2 – 2x + 2x – 2]
= (x2 – 2) [2x2 – 2] 1 = 2(x2 – 2) (x2 – 1)
= 2[x4 – x2 – 2x2 + 2]
= 2[x4 – 3x2 + 2]
= 2x4 – 6x2 + 4
Q.30. If 51x 3 is a multiple of 9, where x is a digit, then that is the value of x ?
Ans. We have, the sum of the digits of 51x 3 = 5 + 1 + x + 3 = 9 + x
Since, 51x 3 is divisible by 9.
∴ (9 + x) must be divisible by 9.
∴ (9 + x) must be equal to 0 or 9 or 18 or 27 or ...
But x is a digit, then
9 + x = 9 ⇒ x = 0
9 + x = 18 ⇒ x = 9
x = 27 ⇒ x = 18, which is not possible.
∴ The required value of x = 0 or 9.
|
81 videos|423 docs|31 tests
|
FAQs on Sample Question Paper- 1 - Mathematics (Maths) Class 8
| 1. What is the importance of solving sample question papers for Class 8 exams? |  |
| 2. How can solving sample question papers help in improving exam performance? |  |
| 3. Where can I find sample question papers for Class 8 exams? |  |
| 4. How should I use sample question papers effectively for exam preparation? |  |
| 5. Are sample question papers enough for Class 8 exam preparation? |  |

















