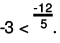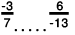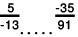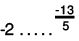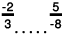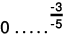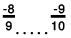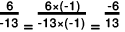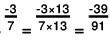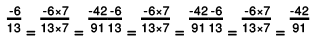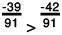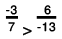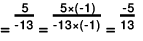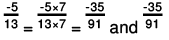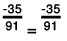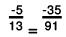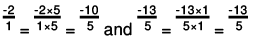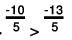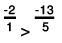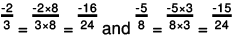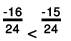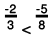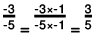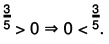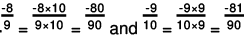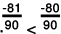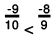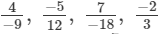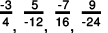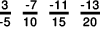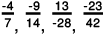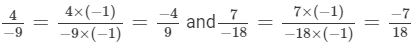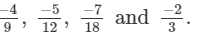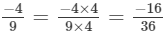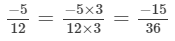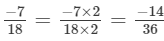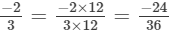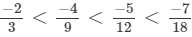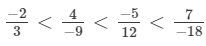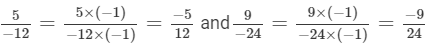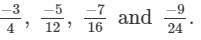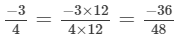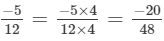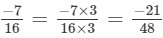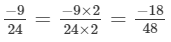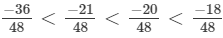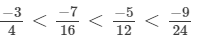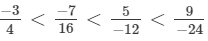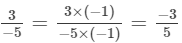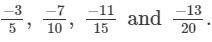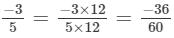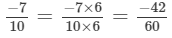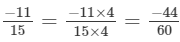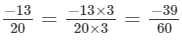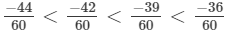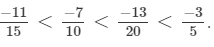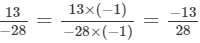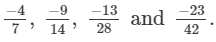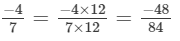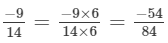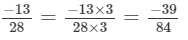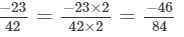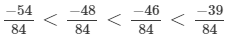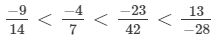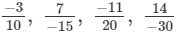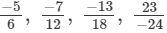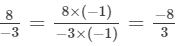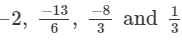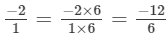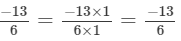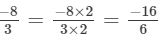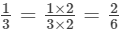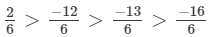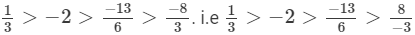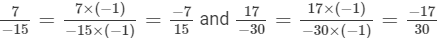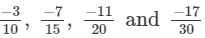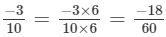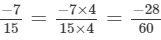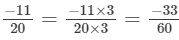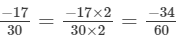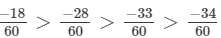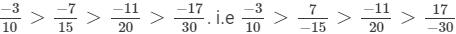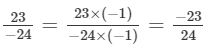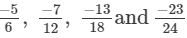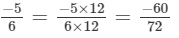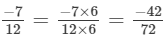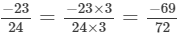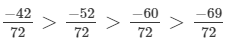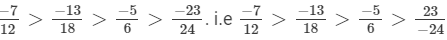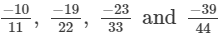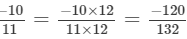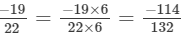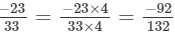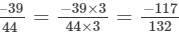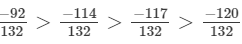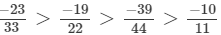Q.1. Express -3/5 as a rational number with denominator
(a) 20
(b) -30
(c) 35
(d) -40
Solution: If a/b is a fraction and m is a non-zero integer, then a/b = 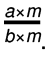
Now,
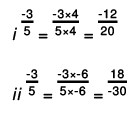
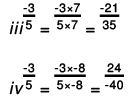
Q.2. Express -42/98 as a rational number with denominator 7.
Solution: If a/b is a rational number and m is a common divisor of a and b, then 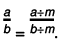
∴ 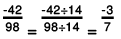
Q.3. Express -48/60 as a rational number with denominator 5.
Solution: If a/b is a rational integer and m is a common divisor of a and b, then 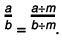
∴ 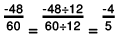
Q.4. Express each of the following rational numbers in standard form:
(a) -12/30
(b) -14/49
(c) 24/-64
(d) -36/-63
Solution: A rational number a/b is said to be in the standard form if a and b have no common divisor other than unity and b > 0.
Thus,
(a) The greatest common divisor of 12 and 30 is 6.
∴ 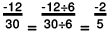 In the standard form
In the standard form
(b) The greatest common divisor of 14 and 49 is 7.
∴ 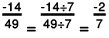 In the standard form
In the standard form
(c) 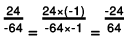
The greatest common divisor of 24 and 64 is 8.
∴ 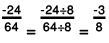 In the standard form
In the standard form
(d) 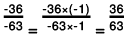
The greatest common divisor of 36 and 63 is 9.
∴ 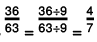 In the standard form
In the standard form
Q.5. Which of the two rational numbers is greater in the given pair?
(a) 3/8 or 0
(b) -2/9 or 0
(c) -3/4 or 1/4
(d) -5/7 or -4/7
(e) 2/3 or 3/4
(f) -1/2 or -1
Solution: We know:
(i) Every positive rational number is greater than 0.
(ii) Every negative rational number is less than 0.
Thus, we have:
(a) 3/8 is a positive rational number.
∴ 3/8 > 0
(b) -2/9 is a negative rational number.
∴ -2/9 < 0
(c) -3/4 is a negative rational number.
∴ -3/4 < 0
Also,
1/4 is a positive rational number.
∴ 1/4 > 0
Combining the two inequalities, we get:
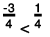
(d) Both -5/7 and -4/7 have the same denominator, that is, 7.
So, we can directly compare the numerators.
∴ 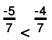
(e) The two rational numbers are 2/3 and 3/4.
The LCM of the denominators 3 and 4 is 12.
Now,
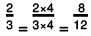
Also,
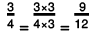
Further
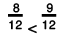
∴ 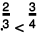
(f) The two rational numbers are -1/2 and -1.
We can write -1 = -1/1.
The LCM of the denominators 2 and 1 is 2.
Now,
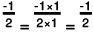
Also,
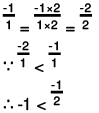
Q.6. Which of the two rational numbers is greater in the given pair?
(a) 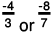
(b) 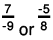
(c) 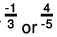
(d) 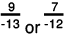
(e) 
(f) 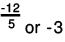
Solution:
(a) The two rational numbers are -4/3 and -8/7.
The LCM of the denominators 3 and 7 is 21.
Now,
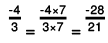
Also,
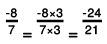
Further,
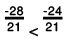
∴ 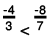
(b) The two rational numbers are 7/-9 and -5/8.
The first fraction can be expressed as 
The LCM of the denominators 9 and 8 is 72.
Now,
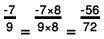
Also,
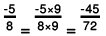
Further,
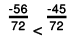
∴ 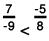
(c) The two rational numbers are -1/3 and 4/-5.
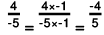
The LCM of the denominators 3 and 5 is 15.
Now,
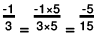
Also,
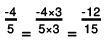
Further,
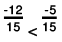
∴ 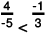
(d) The two rational numbers are 9/-13 and 7/-12.
Now, 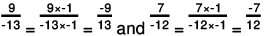
The LCM of the denominators 13 and 12 is 156.
Now,

Also,

Further,

∴ 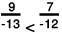
(e) The two rational numbers are 4/-5 and -7/10.
∴ 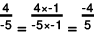
The LCM of the denominators 5 and 10 is 10.
Now,
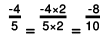
Also,

Further,
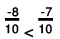
∴ 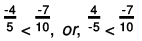
(f) The two rational numbers are -12/5 and -3.
-3 can be written as -3/1.
The LCM of the denominators is 5.
Now,
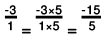
Because 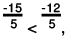 we can conclude that
we can conclude that 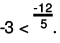
Q.7. Fill in the blanks with the correct symbol out of >, = and <:
(a) 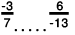
(b) 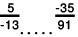
(c) 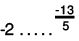
(d) 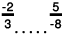
(e) 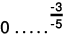
(f) 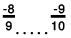
Solution: (a) We will write each of the given numbers with positive denominators.
One number = -3/7
Other number = 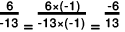
LCM of 7 and 13 = 91
∴ 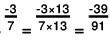
And,
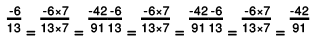
Clearly,
-39 > - 41
∴ 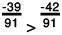
Thus,
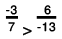
(ii) We will write each of the given numbers with positive denominators.
One number 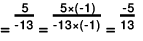
Other number = -35/91
LCM of 13 and 91 = 91
∴ 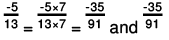
Clearly,
-35 = - 35
∴ 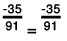
Thus,
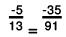
(c) We will write each of the given numbers with positive denominators.
One number = -2
We can write -2 as -2/1.
Other number = -13/5
LCM of 1 and 5 = 5
∴ 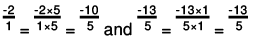
Clearly,
-10 > - 13
∴ 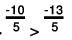
Thus,
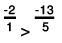
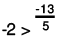
(d) We will write each of the given numbers with positive denominators.
One number = -2/3
Other number = 
LCM of 3 and 8 = 24
∴ 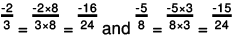
Clearly,
-16 < - 15
∴ 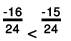
Thus,
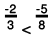

(e) 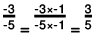
3/5 is a positive number.
Because every positive rational number is greater than 0, 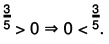
(f) We will write each of the given numbers with positive denominators.
One number = -8/9
Other number = -9/10
LCM of 9 and 10 = 90
∴ 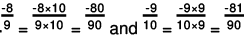
Clearly,
-81 < - 80
∴ 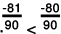
Thus,
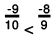
Q.8. Arrange the following rational numbers in ascending order:
(a) 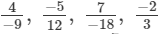
(b) 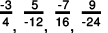
(c) 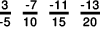
(d) 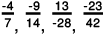
Solution:
(a) We will write each of the given numbers with positive denominators.
We have:
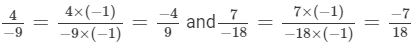
Thus, the given numbers are 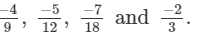
LCM of 9, 12, 18 and 3 is 36.
Now,
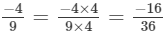
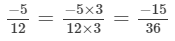
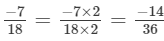
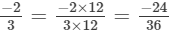
Clearly,

∴ 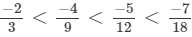
That is
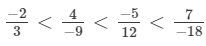
(b) We will write each of the given numbers with positive denominators.
We have:
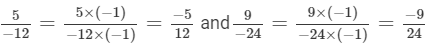
Thus, the given numbers are 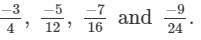
LCM of 4, 12, 16 and 24 is 48.
Now,
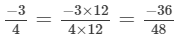
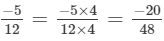
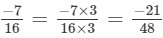
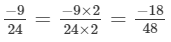
Clearly,
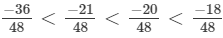
∴ 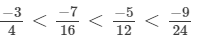
That is
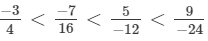
(c) We will write each of the given numbers with positive denominators.
We have:
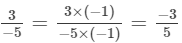
Thus, the given numbers are 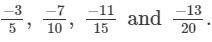
LCM of 5, 10, 15 and 20 is 60.
Now,
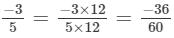
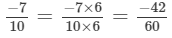
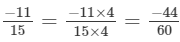
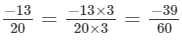
Clearly,
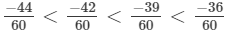
∴ 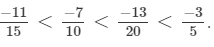
That is

(d) We will write each of the given numbers with positive denominators.
We have:
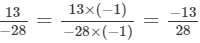
Thus, the given numbers are 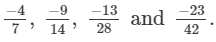
LCM of 7, 14, 28 and 42 is 84.
Now,
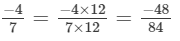
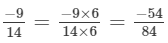
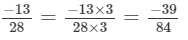
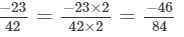
Clearly,
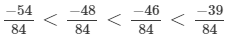
∴ 
That is
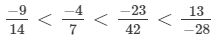
Q.9. Arrange the following rational numbers in descending order:
(a) 
(b) 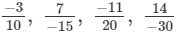
(c) 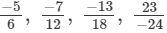
(d) 
Solution:
(a) We will first write each of the given numbers with positive denominators. We have:
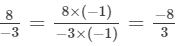
Thus, the given numbers are 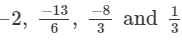
LCM of 1, 6, 3 and 3 is 6
Now,
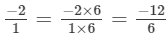
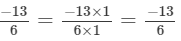
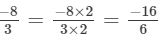
and
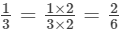
Clearly, Thus,
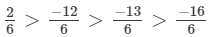
∴ 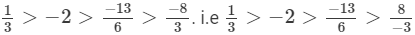
(b) We will first write each of the given numbers with positive denominators. We have:
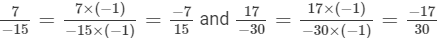
Thus, the given numbers are 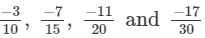
LCM of 10, 15, 20 and 30 is 60
Now,
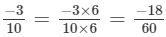
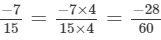
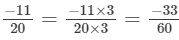
and
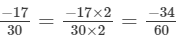
Clearly,
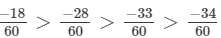
∴ 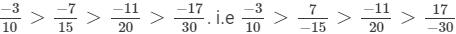
(c) We will first write each of the given numbers with positive denominators. We have:
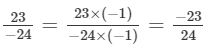
Thus, the given numbers are 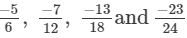
LCM of 6, 12, 18 and 24 is 72
Now,
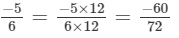
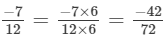
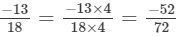
and
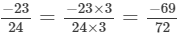
Clearly,
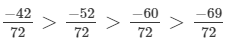
∴ 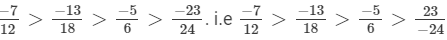
(d) The given numbers are 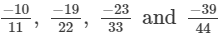
LCM of 11, 22, 33 and 44 is 132
Now,
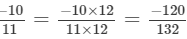
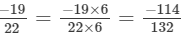
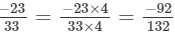
and
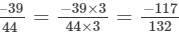
Clearly,
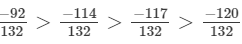
∴ 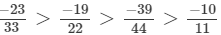
Q.10. Which of the following statements are true and which are false?
(a) Every whole number is a rational number.
(b) Every integer is a rational number.
(c) 0 is a whole number but it is not a rational number.
Solution:
(a) True
A whole number can be expressed as a/b, with b = 1 and a ≥ 0. Thus, every whole number is rational.
(b) True
Every integer is a rational number because any integer can be expressed as a/b, with b = 1 and 0 > a ≥ 0. Thus, every integer is a rational number.
(c) 0 = a/b, for a = 0 and b ≠ 0. Thus, 0 is a rational and whole number.
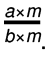
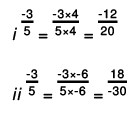
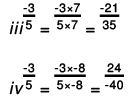
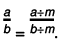
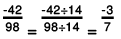
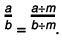
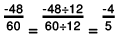
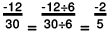 In the standard form
In the standard form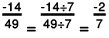 In the standard form
In the standard form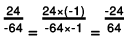
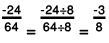 In the standard form
In the standard form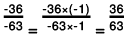
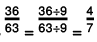 In the standard form
In the standard form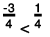
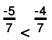
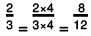
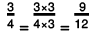
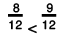
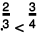
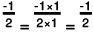
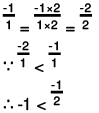
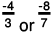
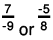
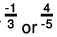
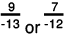

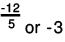
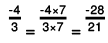
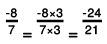
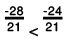
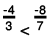

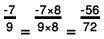
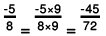
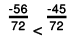
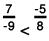
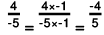
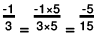
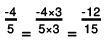
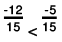
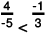
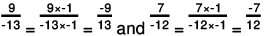



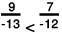
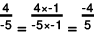
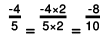

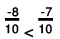
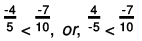
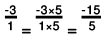
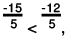 we can conclude that
we can conclude that