RS Aggarwal Solutions: Polynomials- 2 | Mathematics (Maths) Class 9 PDF Download
RS Aggarwal Solutions: Exercise 2B - Polynomials
Q.1. If p(x) = 5 − 4x + 2x2, find (i) p(0), (ii) p(3), (iii) p(−2)
Ans.
(i) p(x)=5−4x+2x2
⇒ p(0)=(5−4×0+2×02)
=(5 − 0 + 0) = 5
= 5
(ii) p(x)=5−4x+2x2
⇒ p(3)=(5−4×3+2×32)
= (5−12+18)
= 11
(iii) p(x)=5−4x+2x2
⇒ p(−2)=[5−4×(−2)+2×(−2)2]
=(5+8+8)
= 21
Q.2. If p(y) = 4 + 3y − y2 + 5y3, find (i) p(0), (ii) p(2), (iii) p(−1).
Ans.
(i) p(y)=4+3y−y2 + 5y3
⇒p(0) = (4 + 3 × 0− 02 + 5 × 03)
=(4 + 0 − 0 + 0)
= 4
(ii) p(y) = 4 + 3y − y2 + 5y3
⇒p(2) = (4 + 3 × 2 − 22 + 5 × 23)
=(4 + 6 − 4 + 40)
= 46
(iii) p(y) = 4 + 3y − y2 + 5y3
⇒ p(−1) = [4 + 3 × (−1) − (−1)2 + 5 × (−1)3]
=(4 − 3 − 1 − 5)
= − 5
Q.3. If f(t) = 4t2 − 3t + 6, find (i) f(0), (ii) f(4), (iii) f(−5).
Ans.
(i) f(t) = 4t2 − 3t + 6
⇒ f(0) = (4 × 02 − 3 × 0 + 6)
= (0 − 0 + 6)
= 6
(ii) f(t) = 4t2 − 3t + 6
⇒ f(4) = (4 × 42 − 3 × 4 + 6)
= (64 − 12 + 6)
= 58
(iii) f(t) = 4t2 − 3t + 6
⇒ f(−5) = [4×(−5)2 − 3× (−5)+6]
=(100+15+6)
=121
Q.4. If p(x)=x3 − 3x2 + 2x, find p(0), p(1), p(2). What do you conclude?
Ans.
p(x) = x3 − 3x2 + 2x .....(1)
Putting x = 0 in (1), we get
p(0) = 03 − 3 × 02 + 2 × 0 = 0
Thus, x = 0 is a zero of p(x).
Putting x = 1 in (1), we get
p(1)=13−3×12+2×1=1−3+2=0
Thus, x = 1 is a zero of p(x).
Putting x = 2 in (1), we get
p(2) = 23−3 × 22 + 2 × 2 = 8 − 3 × 4 + 4 = 8 − 12 + 4 = 0
Thus, x = 2 is a zero of p(x).
Q.5. If p(x) = x3 + x2 – 9x – 9, find p(0), p(3), p(–3) and p(–1). What do you conclude about the zero of p(x)? Is 0 a zero of p(x)?
Ans.
p(x) = x3 + x2 – 9x – 9 .....(1)
Putting x = 0 in (1), we get
p(0) = 03 + 02 – 9 × 0 – 9 = 0 + 0 – 0 – 9 = –9 ≠ 0
Thus, x = 0 is not a zero of p(x).
Putting x = 3 in (1), we get
p(3) = 33 + 32 – 9 × 3 – 9 = 27 + 9 – 27 – 9 = 0
Thus, x = 3 is a zero of p(x).
Putting x = –3 in (1), we get
p(–3) = (–3)3 + (–3)2 – 9 × (–3) – 9 = –27 + 9 + 27 – 9 = 0
Thus, x = –3 is a zero of p(x).
Putting x = –1 in (1), we get
p(–1) = (–1)3 + (–1)2 – 9 × (–1) – 9 = –1 + 1 + 9 – 9 = 0
Thus, x = –1 is a zero of p(x).
Q.6. Verify that:
(i) 4 is a zero of the polynomial p(x) = x − 4.
(ii) −3 is a zero of the polynomial q(x) = x + 3.
(iii) 2/5 is a zero of the polynomial, f(x) = 2 − 5x.
(iv) 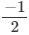 is a zero of the polynomial g(y) = 2y + 1.
is a zero of the polynomial g(y) = 2y + 1.
Ans.
(i) p(x)=x−4
⇒ p(4)=4−4
= 0
Hence, 4 is the zero of the given polynomial.
(ii) p(x) = (−3) + 3
⇒ p(3)=0
Hence, 3 is the zero of the given polynomial.
(iii) p(x) = 2 − 5x
⇒ 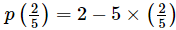
= 2−2
= 0
Hence, 2/5 is the zero of the given polynomial.
(iv) p(y) = 2y + 1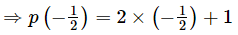
= − 1 + 1
= 0
Hence,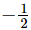 is the zero of the given polynomial.
is the zero of the given polynomial.
Q.7. Verify that
(i) 1 and 2 are the zeros of the polynomial p(x) = x2 − 3x + 2.
(ii) 2 and −3 are the zeros of the polynomial q(x) = x2 + x − 6.
(iii) 0 and 3 are the zeros of the polynomial r(x) = x2 − 3x.
Ans.
(i) p(x)=x2 − 3x + 2 = (x−1) (x−2)
⇒ p(1)=(1−1)×(1−2)
=0×(−1)
=0
Also,
p(2) = (2−1)(2−2)
= (−1) × 0
= 0
Hence, 1 and 2 are the zeroes of the given polynomial.
(ii) p(x) = x2 + x − 6
⇒ p(2) = 22 + 2 − 6
=4 − 4
= 0
Also,
p(−3) = (−3)2 + (−3) − 6
=9 − 9
= 0
Hence, 2 and −3 are the zeroes of the given polynomial.
(iii) p(x) = x2 − 3x
⇒ p (0) = 02 − 3 × 0
Also,
p(3) = 32 − 3 × 3
= 9 − 9
= 0
Hence, 0 and 3 are the zeroes of the given polynomial.
Q.8. Find the zero of the polynomial:
(i) p(x) = x − 5
(ii) q(x) = x + 4
(iii) r(x) = 2x + 5
(iv) f(x) = 3x + 1
(v) g(x) = 5 − 4x
(vi) h(x) = 6x − 2
(vii) p(x) = ax, a ≠ 0
(viii) q(x) = 4x
Ans.
(i) p(x) = 0⇒ x − 5 = 0
⇒ x = 5
Hence, 5 is the zero of the polynomial p(x).
(ii) q(x) = 0 ⇒ x + 4 = 0
⇒x= − 4
Hence, − 4 is the zero of the polynomial q(x).
(iii) r(x) = 0 ⇒ 2x + 5 = 0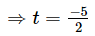
Hence,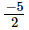 is the zero of the polynomial p(t).
is the zero of the polynomial p(t).
(iv) f(x) = 0 ⇒ 3x + 1 = 0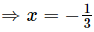
Hence,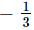 is the zero of the polynomial f(x).
is the zero of the polynomial f(x).
(v) g(x) = 0 ⇒ 5 − 4x = 0
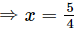
Hence, 5/4 is the zero of the polynomial g(x).
(vi) h (x) = 0 ⇒ 6x − 2 = 0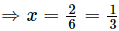
Hence, 1/3 is the zero of the polynomial h(x).
(vii) p(x) = 0 ⇒ ax = 0
⇒ x = 0
Hence, 0 is the zero of the polynomial p(x).
(viii) q(x) = 0 ⇒ 4x = 0
⇒x = 0
Hence, 0 is the zero of the polynomial q(x).
Q.9. If 2 and 0 are the zeros of the polynomial f(x)=2x3−5x2 + ax + b then find the values of a and b.
Hint f(2) = 0 and f(0) = 0.
Ans.
It is given that 2 and 0 are the zeroes of the polynomial f(x)=2x3 − 5x2 + ax + b.
∴ f(2) = 0
⇒2 × 23 − 5 × 22 + a × 2 + b = 0
⇒16 − 20 + 2a + b = 0
⇒ −4 + 2a + b = 0
⇒ 2a + b = 4 .....(1)
Also,
f(0) = 0
⇒ 2 × 03− 5 × 02 + a × 0 + b = 0
⇒ 0 − 0 + 0 + b = 0
⇒ b = 0
Putting b = 0 in (1), we get
2a + 0=4
⇒ 2a = 4
⇒ a = 2
Thus, the values of a and b are 2 and 0, respectively.
RS Aggarwal Solutions: Exercise 2C - Polynomials
Q.1. By actual division, find the quotient and the remainder when (x4 + 1) is divided by (x – 1).
Verify that remainder = f(1).
Ans. Let f(x) = x4 + 1 and g(x) = x – 1.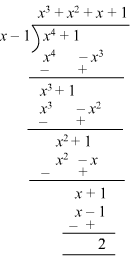
Quotient = x3 + x2 + x + 1
Remainder = 2
Verification:
Putting x = 1 in f(x), we get
f(1) = 14 + 1 = 1 + 1 = 2 = Remainder, when f(x) = x4 + 1 is divided by g(x) = x – 1
Q.2. Verify the division algorithm for the polynomials
p(x)=2x4 − 6x3 + 2x2 − x + 2 and g(x) = x + 2.
Ans.
p(x)=2x4 − 6 x3 + 2x2 −x + 2 and g(x) = x + 2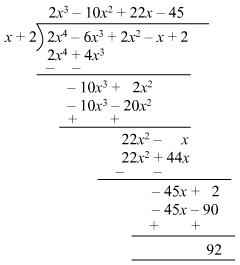
Quotient = 2x3−10x2 + 22x − 45
Remainder = 92
Verification:
Divisor × Quotient + Remainder
=(x+2)×(2x3−10x2 + 22x − 45) + 92
=x(2x3 − 10x2 + 22x − 45) + 2(2x3−10x2+22x − 45) + 92
=2x4 − 10x3 + 22x2 − 45x + 4x3 − 20x2 + 44x − 90 + 92
=2x4 − 6x3 + 2x2 − x + 2
= Dividend
Hence verified.
Q.3. Using the remainder theorem, find the remainder, when p(x) is divided by g(x), where
p(x)=x3−6x2 + 9x + 3, g(x) = x−1.
Ans. p(x)=x3 − 6x2 + 9x + 3
g(x)=x−1
By remainder theorem, when p(x) is divided by (x − 1), then the remainder = p(1).
Putting x = 1 in p(x), we get
p(1)=13 − 6 × 12 + 9 × 1 + 3 = 1 − 6 + 9 + 3 = 7
∴ Remainder = 7
Thus, the remainder when p(x) is divided by g(x) is 7.
Q.4. Using the remainder theorem, find the remainder, when p(x) is divided by g(x), where
p(x)=2x3 − 7x2 + 9x − 13, g(x) = x − 3.
Ans.
p(x)=2x3 − 7x2 + 9x − 13
g(x) = x − 3
By remainder theorem, when p(x) is divided by (x − 3), then the remainder = p(3).
Putting x = 3 in p(x), we get
p(3) = 2×33 − 7×32+9×3−13=54−63+27−13=5
∴ Remainder = 5
Thus, the remainder when p(x) is divided by g(x) is 5.
Q.5. Using the remainder theorem, find the remainder, when p(x) is divided by g(x), where
p(x)=3x4−6x2−8x−2, g(x)=x−2.
Ans.
p(x) = 3x4 − 6x2 − 8x − 2
g(x) = x − 2
By remainder theorem, when p(x) is divided by (x − 2), then the remainder = p(2).
Putting x = 2 in p(x), we get
p(2)=3 × 24 −6 × 22 − 8 × 2 − 2 = 48 − 24− 16 − 2=6
∴ Remainder = 6
Thus, the remainder when p(x) is divided by g(x) is 6.
Q.6. Using the remainder theorem, find the remainder, when p(x) is divided by g(x), where
p(x)=2x3 − 9x2 + x + 15, g(x) = 2x − 3.
Ans.
p(x)=2x3 − 9x2 + x + 15
g(x) = 2x − 3 = 2 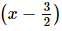
By remainder theorem, when p(x) is divided by (2x − 3), then the remainder = 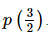
Putting 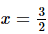 in p(x), we get
in p(x), we get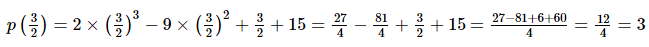
∴ Remainder = 3
Thus, the remainder when p(x) is divided by g(x) is 3.
Q.7. Using the remainder theorem, find the remainder, when p(x) is divided by g(x), where
p(x)=x3 − 2x2− 8x − 1, g(x) = x + 1.
Ans. p(x)=x3−2x2 − 8x − 1
g(x)=x+1
By remainder theorem, when p(x) is divided by (x + 1), then the remainder = p(−1).
Putting x = −1 in p(x), we get
p(−1)=(−1)3−2×(−1)2−8×(−1)−1=−1−2+8−1=4
∴ Remainder = 4
Thus, the remainder when p(x) is divided by g(x) is 4.
Q.8. Using the remainder theorem, find the remainder, when p(x) is divided by g(x), where
p(x) = 2x3 + x2− 15x − 12, g(x) = x + 2.
Ans.
p(x) = 2x3 + x2 −15x − 12
g(x) = x + 2
By remainder theorem, when p(x) is divided by (x + 2), then the remainder = p(−2).
Putting x = −2 in p(x), we get
p(−2) = 2 × (−2)3 + (−2)2 − 15 × (−2) −12 = −16 + 4 + 30 − 12 = 6
∴ Remainder = 6
Thus, the remainder when p(x) is divided by g(x) is 6.
Q.9. Using the remainder theorem, find the remainder, when p(x) is divided by g(x), where
p(x)=6x3 + 13x2 + 3, g(x) = 3x + 2.
Ans.
p(x) = 6x3 + 13x2 + 3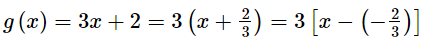
By remainder theorem, when p(x) is divided by (3x + 2), then the remainder = p 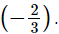
Putting x = 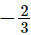 in p(x), we get
in p(x), we get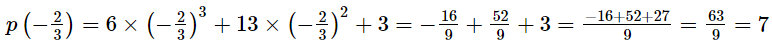
∴ Remainder = 7
Thus, the remainder when p(x) is divided by g(x) is 7.
Q.10. Using the remainder theorem, find the remainder, when p(x) is divided by g(x), where
p(x) = x3 − 6x2 + 2x − 4, g (x) = 1 - 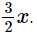
Ans.
p(x)=x3 − 6x2 + 2x − 4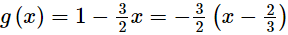
By remainder theorem, when p(x) is divided by 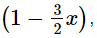 then the remainder =
then the remainder =
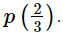
Putting x 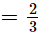 in p(x), we get
in p(x), we get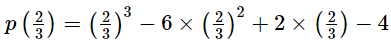
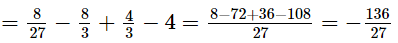
∴ Remainder = 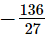
Thus, the remainder when p(x) is divided by g(x) is 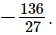
Q.11. Using the remainder theorem, find the remainder, when p(x) is divided by g(x), where
p(x) = 2x3 + 3x2 − 11x − 3, g(x) = 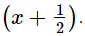
Ans.
p(x) = 2x3 + 3x2 − 11x − 3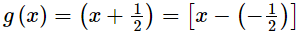
By remainder theorem, when p(x) is divided by 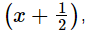 then the remainder =
then the remainder =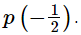
Putting x = 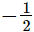 in p(x), we get
in p(x), we get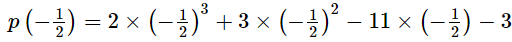
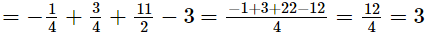
∴ Remainder = 3
Thus, the remainder when p(x) is divided by g(x) is 3.
Q.12. Using the remainder theorem, find the remainder, when p(x) is divided by g(x), where
p(x)=x3 −ax2 + 6x − a, g(x) = x − a.
Ans.
p(x)=x3 − ax2 + 6x − a
g(x) = x − a
By remainder theorem, when p(x) is divided by (x − a), then the remainder = p(a).
Putting x = a in p(x), we get
p(a) = a3 − a × a2 + 6 × a − a = a3 − a3 + 6a − a = 5a
∴ Remainder = 5a
Thus, the remainder when p(x) is divided by g(x) is 5a.
Q.13. The polynomials (2x3 + x2 − ax + 2) and (2x3 − 3x2 −3x + a) when divided by (x – 2) leave the same remainder. Find the value of a.
Ans.
Let f(x) = 2x3 + x2− ax + 2 and g(x)=2x3 − 3x2 − 3x + a.
By remainder theorem, when f(x) is divided by (x – 2), then the remainder = f(2).
Putting x = 2 in f(x), we get
f(2) = 2× 23 + 22 − a × 2 + 2 = 16 + 4 − 2a + 2= −2a + 22
By remainder theorem, when g(x) is divided by (x – 2), then the remainder = g(2).
Putting x = 2 in g(x), we get
g(2) = 2×23 − 3 × 22 − 3 × 2 + a = 16 − 12 − 6 + a = −2 + a
It is given that,
f(2)=g(2)
⇒ −2a + 22 = −2 + a
⇒ −3a = −24
⇒ a = 8
Thus, the value of a is 8.
Q.14. The polynomial p(x) = x4 − 2x3 + 3x2 − ax + b when divided by (x − 1) and (x + 1) leaves the remainders 5 and 19 respectively. Find the values of a and b. Hence, find the remainder when p(x) is divided by (x − 2).
Ans.
Let:
p(x) = x4 − 2x3 + 3x2 − ax + b
Now,
When p(x) is divided by (x−1), the remainder is p(1).
When p(x) is divided by (x+1), the remainder is p(−1).
Thus, we have:
p(1) = (14 − 2 × 13 + 3 × 12 − a × 1 + b)
=(1 − 2 + 3 − a + b)
= 2 − a + b
And,
p(−1)=[(−1)4−2×(−1)3+3×(−1)2−a×(−1)+b]
= (1 + 2 + 3 + a + b)
= 6 + a + b
Now,
2 − a + b = 5 ...(1)
6 + a + b = 19 ...(2)
Adding (1) and (2), we get:
8 + 2b = 24
⇒ 2b = 16
⇒ b = 8
By putting the value of b, we get the value of a, i.e., 5.
∴ a = 5 and b = 8
Now,
f(x) = x4 −2x3 + 3x2 − 5x + 8
Also,
When p(x) is divided by (x−2), the remainder is p(2).
Thus, we have:
p(2)=(24 − 2 × 23+ 3 × 22 − 5 × 2 + 8) [a=5 and b=8]
=(16 − 16 + 12 − 10 + 8)
=10
Q.15. If p(x)=x3 − 5x2 + 4x − 3 and g(x)= x − 2, show that p(x) is not a multiple of g(x).
Ans.
p(x) = x3 − 5x2 + 4x−3
g(x) = x − 2
Putting x = 2 in p(x), we get
p(2) = 23 − 5 × 22 + 4 × 2 − 3 = 8 − 20 + 8 − 3 = − 7 ≠ 0
Therefore, by factor theorem, (x − 2) is not a factor of p(x).
Hence, p(x) is not a multiple of g(x).
Q.16. If p(x) = 2x3 − 11x2 − 4x+5 and g(x) = 2x + 1, show that g(x) is not a factor of p(x).
Ans.
p(x) = 2x3−11x2 − 4x + 5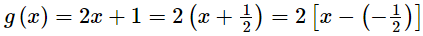
Putting 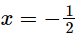 in p(x), we get
in p(x), we get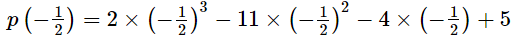
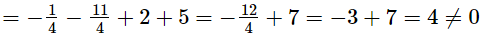
Therefore, by factor theorem, (2x + 1) is not a factor of p(x).
Hence, g(x) is not a factor of p(x).
RS Aggarwal Solutions: Exercise 2D - Polynomials
Q.1. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = x3 – 8, g(x) = x – 2
Ans.
Let:
p(x) = x3 – 8
Now,
g(x) = 0 ⇒ x −2 = 0 ⇒ x =2
By the factor theorem, (x – 2) is a factor of the given polynomial if p(2) = 0.
Thus, we have:
p(2)=(23 − 8)=0
Hence, (x − 2) is a factor of the given polynomial.
Q.2. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 2x3 + 7x2 – 24x – 45, g(x) = x – 3
Ans.
Let:
p(x) = 2x3 + 7x2 – 24x – 45
Now,
x − 3 = 0 ⇒ x = 3
By the factor theorem, (x − 3) is a factor of the given polynomial if p(3) = 0.
Thus, we have:
p(3) = (2 × 33 − 7 × 32 − 24 × 3 − 45)
= (54 + 63 − 72 − 45)
= 0
Hence, (x − 3) is a factor of the given polynomial
Q.3. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 2x4 + 9x3 + 6x2 – 11x – 6, g(x) = x – 1
Ans.
Let:
p(x) = 2x4 + 9x3 + 6x2 – 11x – 6
Here,
x − 1 = 0 ⇒ x=1
By the factor theorem, (x − 1) is a factor of the given polynomial if p(1) = 0.
Thus, we have:
p(1)=(2×14 + 9 × 13 + 6 × 12 − 11 × 1 − 6)
= (2 + 9 + 6 − 11 −6)
= 0
Hence, (x − 1) is a factor of the given polynomial.
Q.4. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = x4 – x2 – 12, g(x) = x + 2
Ans.
Let:
p(x) = x4 – x2 – 12
Here,
x+2 = 0 ⇒ x= −2
By the factor theorem, (x + 2) is a factor of the given polynomial if p (−2) = 0.
Thus, we have:
p(−2) = [(−2)4 − (−2)2 − 12]
= (16 − 4 − 12)
=0
Hence, (x + 2) is a factor of the given polynomial.
Q.5. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 69 + 11x – x2 + x3, g(x) = x + 3
Ans.
p(x)=69+11x−x2+x3
g(x) = x + 3
Putting x = −3 in p(x), we get
p(−3) = 69 + 11 × (−3) − (−3)2 + (−3)3 = 69 − 33 − 9 − 27 = 0
Therefore, by factor theorem, (x + 3) is a factor of p(x).
Hence, g(x) is a factor of p(x).
Q.6. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 2x3 + 9x2 – 11x – 30, g(x) = x + 5
Ans.
Let:
p(x) = 2x3 + 9x2 − 11x − 30
Here,
x + 5 = 0 ⇒ x = −5
By the factor theorem, (x + 5) is a factor of the given polynomial if p (−5) = 0.
Thus, we have:
p(−5) = [2 × (−5)3 +9 × (−5)2 −11 × (−5)−30]
= (−250 + 225 + 55 − 30)
= 0
Hence, (x + 5) is a factor of the given polynomial.
Q.7. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 2x4 + x3 – 8x2 – x + 6, g(x) = 2x – 3
Ans.
Let:
p(x)=2x4 + x3 − 8x2 − x + 6
Here,
2x − 3 = 0 ⇒ x = 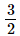
By the factor theorem, (2x − 3) is a factor of the given polynomial if p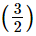 = 0
= 0
Thus, we have: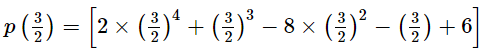
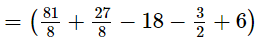
= 0
Hence, (2x − 3) is a factor of the given polynomial.
Q.8. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 3x3 + x2 – 20x + 12, g(x) = 3x – 2
Ans.
p(x) = 3x3 + x2 − 20x + 12
g(x) = 3x − 2 = 3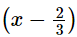
Putting 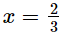 in p(x), we get
in p(x), we get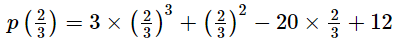
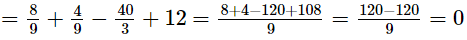
Therefore, by factor theorem, (3x − 2) is a factor of p(x).
Hence, g(x) is a factor of p(x).
Q.9. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 7x2 −4√2x − 6, g(x) = x − √2
Ans.
Let:
p(x)=7x2−4√2x − 6
Here,
x−√2 = 0 ⇒ x = √2
By the factor theorem, (x - √2) is a factor of the given polynomial if p(√2)=0
Thus, we have:
p(√2) = [7×(√2)2 −4√2 × √2 −6]
=(14 − 8 − 6)
= 0
Hence, (x − √2) is a factor of the given polynomial.
Q.10. Using factor theorem, show that g(x) is a factor of p(x), when
p(x)=2√2x2 + 5x + √2, g(x) =x + √2
Ans.
Let:
p(x)=2√2x2 + 5x + √2
Here,
x + √2 = 0 ⇒ x = −√2
By the factor theorem, (x+√2) will be a factor of the given polynomial if p(−√2) = 0.
Thus, we have:
p(−√2) = [2√2 × (−√2)2 + 5 × (−√2)+√2]
=(4√2−5√2+√2)
= 0
Hence, (x + √2) is a factor of the given polynomial.
Q.11. Show that (p – 1) is a factor of (p10 – 1) and also of (p11 – 1).
Ans.
Let f(p) = p10 – 1 and g(p) = p11 – 1.
Putting p = 1 in f(p), we get
f(1) = 110 − 1 = 1 − 1 = 0
Therefore, by factor theorem, (p – 1) is a factor of (p10 – 1).
Now, putting p = 1 in g(p), we get
g(1) = 111 − 1 = 1 − 1 = 0
Therefore, by factor theorem, (p – 1) is a factor of (p11 – 1).
Q.12. Find the value of k for which (x − 1) is a factor of (2x3 + 9x2 + x + k).
Ans.
Let:
f(x)=2x3 + 9x2 + x + k
(x−1) is a factor of f(x) = 2x3 + 9x2 + x + k.
⇒ f(1) = 0
⇒2 × 13 + 9 × 12 + 1 + k = 0
⇒12 + k = 0
⇒k= −12
Hence, the required value of k is −12.
Q.13. Find the value of a for which (x − 4) is a factor of (2x3 − 3x2 − 18x + a).
Ans.
Let:
f(x)=2x3 − 3x2 − 18x + a
(x−4) is a factor of f(x)=2x3 − 3x2 − 18x + a.
⇒ f(4) = 0
⇒2 × 43 − 3 × 42 − 18 × 4 + a = 0
⇒8 + a = 0 ⇒ a = −8
Hence, the required value of a is −8.
Q.14. Find the value of a for which (x + 1) is a factor of (ax3 + x2 – 2x + 4a – 9).
Ans.
Let f(x) = ax3 + x2 – 2x + 4a – 9
It is given that (x + 1) is a factor of f(x).
Using factor theorem, we have
f(−1) = 0
⇒a×(−1)3+(−1)2−2×(−1) + 4a − 9 = 0
⇒− a + 1 + 2+ 4a −9 = 0
⇒ 3a −6 = 0
⇒ 3a = 6
⇒a = 2
Thus, the value of a is 2.
Q.15. Find the value of a for which (x + 2a) is a factor of (x5 – 4a2 x3 + 2x + 2a +3).
Ans.
Let f(x) = x5 – 4a2 x3 + 2x + 2a +3
It is given that (x + 2a) is a factor of f(x).
Using factor theorem, we have
f(−2a) = 0
⇒(−2a)5−4a2×(−2a)3+2×(−2a)+2a+3=0
⇒−32a5−4a2×(−8a3)+2×(−2a)+2a+3=0
⇒−32a5+32a5−4a+2a+3=0
⇒ −2a + 3 = 0
⇒ 2a = 3
⇒ 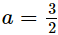
Thus, the value of a is 3/2.
Q.16. Find the value of m for which (2x – 1) is a factor of (8x4 + 4x3 – 16x2 + 10x + m).
Ans.
Let f(x) = 8x4 + 4x3 – 16x2 + 10x + m
It is given that (2x−1) = 2 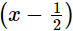 is a factor of f(x).
is a factor of f(x).
Using factor theorem, we have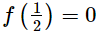
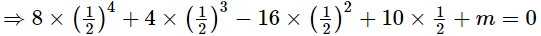
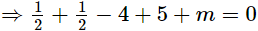
⇒2 + m = 0
⇒m = −2
Thus, the value of m is −2.
Q.17. Find the value of a for which the polynomial (x4 − x3 − 11x2 − x + a) is divisible by (x + 3).
Ans.
Let:
f(x) = x4 − x3 − 11x2 − x + a
Now,
x + 3 = 0 ⇒ x = −3
By the factor theorem, f(x) is exactly divisible by (x+3) if f (−3) = 0.
Thus, we have:
f(−3) = [(−3)4−(−3)3−11×(−3)2−(−3)+a]
=(81 + 27 − 99 + 3 + a)
=12 + a
Also,
f( − 3) = 0
⇒ 12 + a = 0
⇒ a = −12
Hence, f(x) is exactly divisible by (x+3) when a is −12.
Q.18. Without actual division, show that (x3 − 3x2 − 13x + 15) is exactly divisible by (x2 + 2x − 3).
Let:
f(x)=x3 − 3x2 −13 x + 15
And,
g(x) = x2 + 2x − 3
=x2 + x − 3x −3
=x(x − 1)+3(x − 1)
=(x − 1)(x + 3)
Now, f(x) will be exactly divisible by g(x) if it is exactly divisible by (x−1) as well as (x+3).
For this, we must have:
f(1) = 0 and f(−3) = 0
Thus, we have:
f(1) = (13 − 3 × 12 − 13 × 1 + 15)
=(1 − 3 − 13 + 15)
= 0
And,
f(−3)=[(−3)3−3×(−3)2−13×(−3)+15]
=(−27−27+39+15)
= 0
f(x) is exactly divisible by (x−1) as well as (x+3) . So, f(x) is exactly divisible by (x−1)(x+3).
Hence, f(x) is exactly divisible by x2 + 2x − 3.
Q.19. If (x3 + ax2 + bx + 6) has (x − 2) as a factor and leaves a remainder 3 when divided by (x − 3), find the values of a and b.
Ans.
Let:
f(x)=x3 + ax2 + bx + 6
(x−2) is a factor of f(x)=x3 + ax2 + bx + 6.
⇒f(2) = 0
⇒23 + a × 22 + b × 2 + 6 = 0
⇒14 + 4a + 2b =0
⇒4a + 2b = −14
⇒ 2a + b= −7 ...(1)
Now,
x − 3 = 0 ⇒ x = 3
By the factor theorem, we can say:
When f(x) will be divided by (x−3), 3 will be its remainder.
⇒ f(3) = 3
Now,
f(3)=33 + a × 32 + b × 3 + 6
=(27 + 9a + 3b + 6)
= 33 + 9a + 3b
Thus, we have:
f (3) = 3
⇒33 + 9a + 3b = 3
⇒9a + 3b = −30
⇒3a + b = −10 ...(2)
Subtracting (1) from (2), we get:
a = −3
By putting the value of a in (1), we get the value of b, i.e., −1.
∴ a = −3 and b = −1
Q.20. Find the values of a and b so that the polynomial (x3 − 10x2 + ax + b) is exactly divisible by (x −1) as well as (x − 2).
Ans.
Let:
f(x) =x3 − 10 x2 + ax + b
Now,
x − 1 = 0 ⇒ x = 1
By the factor theorem, we can say:
f(x) will be exactly divisible by (x − 1) if f(1) = 0
Thus, we have:
f(1)=13 − 10 × 12 + a × 1 + b
=(1 − 10 + a + b)
= −9 + a + b
∴ f(1) = 0 ⇒ a + b = 9 ...(1)
Also,
x − 2 = 0 ⇒ x = 2
By the factor theorem, we can say:
f(x) will be exactly divisible by (x−2) if f(2)=0.
Thus, we have:
f(2)=23 − 10 × 22 + a × 2 + b
=(8 − 40 + 2a + b)
= − 32 + 2a + b
∴ f(2) = 0 ⇒ 2a+b=32 ...(2)
Subtracting (1) from (2), we get:
a = 23
Putting the value of a, we get the value of b, i.e., −14.
∴ a = 23 and b = −14
Q.21. Find the values of a and b so that the polynomial (x4 + ax3 − 7x2 − 8x + b) is exactly divisible by (x + 2) as well as (x + 3).
Ans.
Let:
f(x)=x4 + ax3 − 7x2 − 8x + b
Now,
x + 2 = 0 ⇒ x = −2
By the factor theorem, we can say:
f(x) will be exactly divisible by (x+2) if f(−2)=0 .
Thus, we have:
f(−2)=[(−2)4+a×(−2)3−7×(−2)2−8×(−2)+b]
=(16 − 8a − 28 +16+ b)
=(4 − 8a + b)
∴ f(−2) = 0 ⇒ 8a − b = 4 ...(1)
Also,
x + 3 = 0 ⇒ x = −3
By the factor theorem, we can say:
f(x) will be exactly divisible by (x+3) if f(−3)=0 .Thus, we have:
f(−3) = [(−3)4+a×(−3)3−7×(−3)2−8×(−3)+b
=(81 −27a − 63 + 24 + b)
= (42 − 27 a + b)
∴ f(−3) = 0 ⇒ 27a − b = 42 ...(2)
Subtracting (1) from (2), we get:
⇒19a = 38
⇒ a = 2
Putting the value of a, we get the value of b, i.e., 12.
∴ a = 2 and b = 12
Q.22. If both (x – 2) and 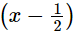 are factors of px2 + 5x + r, prove that p = r.
are factors of px2 + 5x + r, prove that p = r.
Ans.
Let f(x) = px2 + 5x + r
It is given that (x – 2) is a factor of f(x).
Using factor theorem, we have
f(2) = 0
⇒p × 22 + 5 × 2 + r = 0
⇒ 4p + r= −10 .....(1)
Also,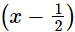 is a factor of f(x).
is a factor of f(x).
Using factor theorem, we have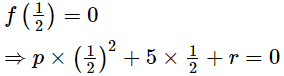
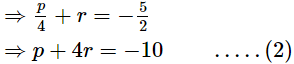
From (1) and (2), we have
4p + r = p + 4r
⇒ 4p − p= 4r − r
⇒3p = 3r
⇒ p = r
Q.23. Without actual division, prove that 2x4 – 5x3 + 2x2 – x + 2 is divisible by x2 – 3x + 2.
Ans.
Let f(x) = 2x4 – 5x3 + 2x2 – x + 2 and g(x) = x2 – 3x + 2.
x2 − 3x + 2
=x2 − 2x − x + 2
= x(x − 2) − 1(x − 2)
=(x−1)(x − 2)
Now, f(x) will be divisible by g(x) if f(x) is exactly divisible by both (x − 1) and (x − 2).
Putting x = 1 in f(x), we get
f(1) = 2 × 14 – 5 × 13 + 2 × 12 – 1 + 2 = 2 – 5 + 2 – 1 + 2 = 0
By factor theorem, (x − 1) is a factor of f(x). So, f(x) is exactly divisible by (x − 1).
Putting x = 2 in f(x), we get
f(2) = 2 × 24 – 5 × 23 + 2 × 22 – 2 + 2 = 32 – 40 + 8 – 2 + 2 = 0
By factor theorem, (x − 2) is a factor of f(x). So, f(x) is exactly divisible by (x − 2).
Thus, f(x) is exactly divisible by both (x − 1) and (x − 2).
Hence, f(x) = 2x4 – 5x3 + 2x2 – x + 2 is exactly divisible by (x − 1)(x − 2) = x2 – 3x + 2.
Q.24. What must be added to 2x4 – 5x3 + 2x2 – x – 3 so that the result is exactly divisible by (x – 2)?
Ans.
Let k be added to 2x4 – 5x3 + 2x2 – x – 3 so that the result is exactly divisible by (x – 2). Here, k is a constant.
∴ f(x) = 2x4 – 5x3 + 2x2 – x – 3 + k is exactly divisible by (x – 2).
Using factor theorem, we have
f(2)=0
⇒2×24−5×23+2×22−2−3+k=0
⇒32 − 40 + 8 − 5 + k = 0
⇒ −5 + k = 0
⇒k = 5
Thus, 5 must be added to 2x4 – 5x3 + 2x2 – x – 3 so that the result is exactly divisible by (x – 2).
Q.25. What must be subtracted from (x4 + 2x3 – 2x2 + 4x + 6) so that the result is exactly divisible by (x2 + 2x – 3)?
Ans.
Dividing (x4 + 2x3 – 2x2 + 4x + 6) by (x2 + 2x – 3) using long division method, we have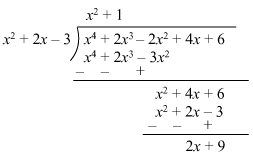
Here, the remainder obtained is (2x + 9).
Thus, the remainder (2x + 9) must be subtracted from (x4 + 2x3 – 2x2 + 4x + 6) so that the
result is exactly divisible by (x2 + 2x – 3).
Q.26. Use factor theorem to prove that (x + a) is a factor of (xn + an) for any odd positive integer.
Ans.
Let f(x) = xn + an
Putting x = −a in f(x), we get
f(−a) = (−a)n + an
If n is any odd positive integer, then
f(−a) = (−a)n + an = −an + an = 0
Therefore, by factor theorem, (x + a) is a factor of (xn + an) for any odd positive integer.
|
40 videos|563 docs|57 tests
|
FAQs on RS Aggarwal Solutions: Polynomials- 2 - Mathematics (Maths) Class 9
| 1. What are the RS Aggarwal Solutions? |  |
| 2. What is Exercise 2B - Polynomials in RS Aggarwal Solutions? |  |
| 3. What is the purpose of Exercise 2C - Polynomials in RS Aggarwal Solutions? |  |
| 4. What does Exercise 2D - Polynomials in RS Aggarwal Solutions cover? |  |
| 5. Are the RS Aggarwal Solutions for Polynomials-2 suitable for competitive exams? |  |
















