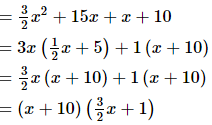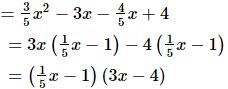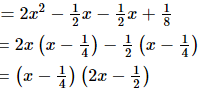Q.1. Factorize: x2 + 11x + 30
Ans. We have:
x2+11x+30
We have to split 11 into two numbers such that their sum of is 11 and their product is 30.
Clearly, 5+6=11 and 5×6=30.
∴ x2+11x+30
= x2+5x+6x+30
= x(x+5)+6(x+5)
=(x+5)(x+6)
Q.2. Factorize: x2 + 18x + 32
Ans. We have:
x2+18x+32
We have to split 18 into two numbers such that their sum is 18 and their product is 32.
Clearly, 16+2=18 and 16×2=32.
∴x2+18x+32
=x2+16x+2x+32
=x(x+16)+2(x+16)
=(x+16)(x+2)
Q.3. Factorise: x2 + 20x – 69
Ans. x2+20x-69
=x2+23x-3x-69
=x(x+23)-3(x+23)
=(x+23)(x-3)
Q.4. x2 + 19x – 150
Ans. x2+19x-150
=x2+25x-6x-150
=x(x+25)-6(x+25)
=(x+25)(x-6)
Q.5. Factorise: x2 + 7x – 98
Ans. x2+7x-98
=x2+14x-7x-98
=x(x+14)-7(x+14)
=(x+14)(x-7)
Q.6. Factorise: x2+2√3x–24
Ans. x2+2√3x–24
= x2+4√3x-2√3x-24
= x(x+4√3)-2√3(x+4√3)
=(x+4√3)(x-2√3)
Q.7. Factorise: x2 – 21x + 90
Ans. x2-21x+90
=x2-15x-6x+90
=x(x-15)-6(x-15)
=(x-6)(x-15)
Q.8. Factorise: x2 – 22x + 120
Ans. x2-22x+120
=x2-12x-10x+120
=x(x-12)-10(x-12)
=(x-10)(x-12)
Q.9. Factorise: x2 – 4x + 3
Ans. x2-4x+3
=x2-3x-x+3
=x(x-3)-1(x-3)
=(x-1)(x-3)
Q.10. Factorise: x2+7√6x+60
Ans. x2+7√6x+60
=x2+5√6x+2√6x+60
=x(x+5√6)+2√6(x+5√6)=(x+5√6)(x+2√6)
Q.11. Factorise: x2+3√3x+6
Ans. x2+3√3x+6
=x2+2√3x+√3x+6
=x(x+2√3)+√3(x+2√3)
=(x+2√3)(x+√3)
Q.12. Factorise: x2+6√6x+48
Ans. x2+6√6x+48
=x2+4√6x+2√6x+48
=x(x+4√6)+2√6(x+4√6)
=(x+4√6)(x+2√6)
Q.13. Factorise: x2+5√5x+30
Ans. x2+5√5x+30
=x2+3√5x+2√5x+30
=x(x+3√5)+2√5(x+3√5)=(x+3√5)(x+2√5)
Q.14. Factorise: x2-24x-180
Ans. x2-24x-180
=x2-30x+6x-180
=x(x-30)+6(x-30)
=(x-30)(x+6)
Q.15. Factorise: x2 – 32x – 105
Ans. x2-32x-105
=x2-35x+3x-105
=x(x-35)+3(x-35)
=(x-35)(x+3)
Q.16. Factorise: x2 – 11x – 80
Ans. x2-11x-80
=x2-16x+5x-80
=x(x-16)+5(x-16)
=(x-16)(x+5)
Q.17. Factorise: 6 – x – x2
Ans. -x2-x+6
=-x2-3x+2x+6
=-x(x+3)+2(x+3)
=(x+3)(-x+2)
=(x+3)(2-x)
Q.18. Factorise: x2-√3x-6
Ans. x2-√3x-6
=x2-2√3x+√3x-6
=x(x-2√3)+√3(x-2√3)
=(x-2√3)(x+√3)
Q.19. Factorise: 40 + 3x – x2
Ans. -x2+3x+40
=-x2+8x-5x+40
=-x(x-8)-5(x-8)
=(x-8)(-x-5)
=(8-x)(x+5)
Q.20. Factorise: x2 – 26x + 133
Ans. x2-26x+133
=x2-19x-7x+133
=x(x-19)-7(x-19)
=(x-19)(x-7)
Q.21. Factorise: x2-2√3x-24
Ans. x2-2√3x-24
=x2-4√3x+2√3x-24
=x(x-4√3)+2√3(x-4√3)
=(x-4√3)(x+2√3)
Q.22. Factorise: x2-3√5x-20
Ans. x2-3√5x-20
=x2-4√5x+√5x-20
=x(x-4√5)+√5(x-4√5)
=(x-4√5)(x+√5)
Q.23. Factorise: x2+√2x-24
Ans. x2+√2x-24
=x2+4√2x-√2x-24
=x(x+4√2)-3√2(x+4√2)
=(x+4√2)(x-3√2)
Q.24. Factorise: x2-2√2x-30
Ans. x2-2√2x-30
=x2-5√2x+3√2x-30
=x(x-5√2)+3√2(x-5√2)
=(x-5√2)(x+3√2)
Q.25. Factorize: x2 − x − 156
Ans. We have: x2-x-156
We have to split (-1) into two numbers such that their sum is (-1) and their product is (-156).
Clearly, -13+12=-1 and -13×12=-156.
∴x2-x-156
=x2-13x+12x-156
=x(x-13)+12(x-13)
=(x-13)(x+12)
Q.26. Factorise: x2 – 32x – 105
Ans. x2-32x-105
=x2-35x+3x-105
=x(x-35)+3(x-35)
=(x-35)(x+3)
Q.27. Factorise: 9x2 + 18x + 8
Ans. 9x2+18x+8
=9x2+12x+6x+8
=3x(3x+4)+2(3x+4)
=(3x+4)(3x+2)
Q.28. Factorise: 6x2 + 17x + 12
Ans. 6x2+17x+12
=6x2+9x+8x+12
=3x(2x+3)+4(2x+3)
=(2x+3)(3x+4)
Q.29. Factorize: 18x2 + 3x − 10
Ans. We have: 18x2+3x-10
We have to split 3 into two numbers such that their sum is 3 and their product is (-180), i.e., 18×(-10).
Clearly, 15+(-12)=3 and 15×(-12)=-180.
∴18x2+3x-10
=18x2+15x-12x-10
=3x(6x+5)-2(6x+5)
=(6x+5)(3x-2)
Q.30. Factorize: 2x2 + 11x − 21
Ans. We have: 2x2+11x-21
We have to split 11 into two numbers such that their sum is 11 and their product is (-42),
i.e., 2×(-21).
Clearly, 14+(-3)
=11 and 14×(-3)
=-42.
∴2x2+11x-21
=2x2+14x-3x-21
=2x(x+7)-3(x+7)
=(x+7)(2x-3)
Q.31. Factorize: 15x2 + 2x − 8
Ans. We have: 15x2+2x-8
We have to split 2 into two numbers such that their sum is 2 and their product is (-120), i.e., 15×(-8).
Clearly, 12+(-10)=2
and 12×(-10)=-120.
∴15x2+2x-8
=15x2+12x-10x-8
=3x(5x+4)-2(5x+4)
=(5x+4)(3x-2)
Q.32. Factorise: 21x2 + 5x – 6
Ans. 21x2+5x-6
=21x2+14x-9x-6
=7x(3x+2)-3(3x+2)
=(3x+2)(7x-3)
Q.33. Factorize: 24x2 − 41x + 12
Ans. We have: 24x2-41x+12
We have to split (-41) into two numbers such that their sum is (-41) and their product is 288, i.e., 24×12.
Clearly, (-32)+(-9)=-41 and (-32)×(-9)=288.
∴24x2-41x+12
=24x2-32x-9x+12
=8x(3x-4)-3(3x-4)
=(3x-4)(8x-3)
Q.34. Factorise: 3x2 – 14x + 8
Ans. 3x2-14x+8
=3x2-12x-2x+8
=3x(x-4)-2(x-4)
=(x-4)(3x-2)
Hence, factorisation of 3x2 – 14x + 8 is (x-4)(3x-2).
Q.35. Factorize: 2x2 + 3x − 90
Ans. We have: 2x2+3x-90
We have to split 3 into two numbers such that their sum is 3 and their product is (-180), i.e., 2×(-90).
Clearly, -12 + 15 = 3 and -12×15 = -180.
∴2x2+3x-90
=2x2-12x+15x-90
=2x(x-6)+15(x-6)
=(x-6)(2x+15)
Q.36. Factorize: √5x2+2x-3√5
Ans. We have:√5x2+2x-3√5
We have to split 2 into two numbers such that their sum is 2 and product is (-15), i.e.,√5×(-3√5).
Clearly, 5+(-3)=2 and 5×(-3)=-15.
∴√5x2+2x-3√5
=√5x2+5x-3x-3√5
=√5x(x+√5)-3(x+√5)
=(x+√5)(√5x-3)
Q.37. Factorize: 2√3x2+x-5√3
Ans. We have: 2√3x2+x-5√3
We have to split 1 into two numbers such that their sum is 1 and product is 30, i.e.,2√3×(-5√3).
Clearly, 6+(-5)=1 and 6×(-5)=-30.
∴2√3x2+x-5√3
=2√3x2+6x-5x-5√3
=2√3x(x+√3)-5(x+√3)
=(x+√3)(2√3x-5)
Q.38. Factorize: 7x2+2√14x+2
Ans. We have: 7x2+2√14x+2
We have to split 2√14 into two numbers such that their sum is 2√14 and product is 14.
Clearly, √14+√14=2
√14 and √14×√14=14.
∴7x2+2√14x+2
=7x2+√14x+√14x+2
=√7x(√7x+√2)+√2(√7x+√2)
=(√7x+√2)(√7x+√2)
=(√7x+√2)2
Q.39. Factorize: 6√3x2-47x+5√3
Ans. We have: 6√3x2-47x+5√3
Now, we have to split (-47) into two numbers such that their sum is (-47) and their product is 90.
Clearly, (-45)+(-2)=-47 and (-45)×(-2)=90.
∴6√3x2-47x+5√3
=6√3x2-2x-45x+5√3
=2x(3√3x-1)-5√3(3√3x-1)
=(3√3x-1)(2x-5√3)
Q.40. Factorize: 5√5x2+20x+3√5
Ans. We have: 5√5x2+20x+3√5
We have to split 20 into two numbers such that their sum is 20 and their product is 75.
Clearly, 15+5=20 and 15×5=75
∴5√5x2+20x+3√5
=5√5x2+15x+5x+3√5
=5x(√5x+3)+√5(√5x+3)
=(√5x+3)(5x+√5)
Q.41. Factorise: √3x2+10x+8√3
Ans. √3x2+10x+8√3
=√3x2+6x+4x+8√3
=√3x(x+2√3)+4(x+2√3)
=(x+2√3)(√3x+4)
Hence, factorisation of √3x2+10x+8√3 is (x+2√3)(√3x+4).
Q.42. Factorize: √2x2+3x+√2
Ans. We have: √2x2+3x+√2
We have to split 3 into two numbers such that their sum is 3 and their product is 2, i.e.,
√2×√2.
Clearly, 2+1=3 and 2×1=2.
∴√2x2+3x+√2
=√2x2+2x+x+√2
=√2x(x+√2)+1(x+√2)
=(x+√2)(√2x+1)
Q.43. Factorize: 2x2+3√3x+3
Ans. We have: 2x2+3√3x+3
We have to split 3√3 into two numbers such that their sum is 3√3 and their product is 6, i.e.,2×3.
Clearly, 2√3+√3=3√3 and 2√3×√3=6.
∴2x2+3√3x+3=2x2+2√3x+√3x+3
=2x(x+√3)+√3(x+√3)
=(x+√3)(2x+√3)
Q.44. Factorize: 15x2 − x − 128
Ans. We have: 15x2-x-28
We have to split (-1) into two numbers such that their sum is (-1) and their product is (-420), i.e., 15×(-28).
Clearly, (-21)+20=-1 and (-21)×20=-420.
∴15x2-x-28
=15x2-21x+20x-28
=3x(5x-7)+4(5x-7)
=(5x-7)(3x+4)
Q.45. Factorize: 6x2 − 5x − 21
Ans. We have: 6x2-5x-21
We have to split (-5) into two numbers such that their sum is (-5) and their product is (-126), i.e., 6×(-21).
Clearly, 9+(-14)=-5 and 9×(-14)=-126.
∴6x2-5x-21
=6x2+9x-14x-21
=3x(2x+3)-7(2x+3)
=(2x+3)(3x-7)
Q.46. Factorize: 2x2 − 7x − 15
Ans. We have: 2x2-7x-15
We have to split (-7) into two numbers such that their sum is (-7) and their product is (-30), i.e., 2×(-15).
Clearly, (-10)+3=-7 and (-10)×3=-30.
∴2x2-7x-15
=2x2-10x+3x-15
=2x(x-5)+3(x-5)
=(x-5)(2x+3)
Q.47. Factorize: 5x2 − 16x − 21
Ans. We have: 5x2-16x-21
We have to split (-16) into two numbers such that their sum is (-16) and their product is (-105), i.e., 5×(-21).
Clearly, (-21)+5=-16 and (-21)×5=-105.
∴ 5x2-16x-21
=5x2+5x-21x-21
=5x(x+1)-21(x+1)
=(x+1)(5x-21)
Q.48. Factorise: 6x2 – 11x – 35
Ans. 6x2-11x-35
=6x2-21x+10x-35
=3x(2x-7)+5(2x-7)
=(2x-7)(3x+5)
Hence, factorisation of 6x2 – 11x – 35 is (2x-7)(3x+5).
Q.49. Factorise: 9x2 – 3x – 20
Ans. 9x2-3x-20
=9x2-15x+12x-20
=3x(3x-5)+4(3x-5)
=(3x-5)(3x+4)
Hence, factorisation of 9x2 – 3x – 20 is (3x-5)(3x+4).
Q.50. Factorize: 10x2 − 9x − 7
Ans. We have: 10x2-9x-7
We have to split (-9) into two numbers such that their sum is (-9) and their product is (-70), i.e., 10×(-7).
Clearly, (-14)+5=-9 and (-14)×5=-70.
∴10x2-9x-7
=10x2+5x-14x-7
=5x(2x+1)-7(2x+1)
=(2x+1)(5x-7)
Q.51. Factorize: x2-2x+7/16
Ans. We have:x2-2x+716
= (16x2-32x+7)/16
= 1/16 (16x2-32x+7)
Now, we have to split (-32) into two numbers such that their sum is (-32) and their product is 112, i.e., 16×7.
Clearly, (-4)+(-28)=-32 and (-4)×(-28)=112.
∴x2 - 2x + 7/16 = 1/16 (16x2-32x+7)
= 1/16 (16x2-4x-28x+7)
= 1/16 [4x(4x-1)-7(4x-1)]
= 1/16 (4x-1)(4x-7)
Q.52. Factorise: (1/3)x2-2x-9
Ans. (1/3)x2-2x-9 = (x2-6x-27)/3
= (x2-9x+3x-27)/3
= (x(x-9)+3(x-9))/3
= ((x-9)(x+3))/3
= (x-9)/3×(x+3)/1
=(1/3x-3)(x+3)
Hence, factorisation of (1/3) x2-2x-9 is (1/3x-3)(x+3).
Q.53. Factorise: x2+ 12/35 x+1/35
Ans. x2+ 12/35x+ 1/35
= (35x2+12x+1)/35
= (35x2+7x+5x+1)/35
= (7x(5x+1)+1(5x+1))/35= ((5x+1)(7x+1))/35
= (5x+1)/5 x (7x+1)/7
= (x+1/5) × (x+1/7)
Hence, factorisation of x2+12/35x+1/35is (x+1/5)(x+1/7).
Q.54. Factorise: 21x2-2x+ 1/21
Ans. 21x2-2x+1/21
=21x2-x-x+1/21
=21x(x-1/21)-1(x-1/21)
=(x-1/21)(21x-1)
Hence, factorisation of 21x2-2x+1/21 is (x-1/21)(21x-1).
Q.55. Factorise: 3/2 x2+16x+10
Ans. 3/2 x2+16x+10
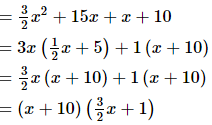
Hence, factorisation of 3/2 x2+16x+10 is (x+10)(3/2x+1).
Q.56. Factorise: 2/3x2 - 17/3x-28
Ans. 2/3x2-17/3 x-28

Hence, factorisation of 2/3 x2- 17/3 x-28 is (1/3x-4)(2x+7).
Q.57. Factorise: 3/5 x2-19/5x+4
Ans. 3/5 x2-19/5 x+4
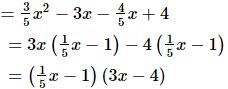
Hence, factorisation of 3/5 x2- 19/5 x+4 is (1/5 x-1)(3x-4).
Q.58. Factorise: 2x2-x+1/8
Ans. 2x2-x+1/8
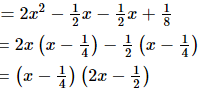
Hence, factorisation of 2x2-x+1/8 is (x-1/4)(2x-1/2).
Q.59. Factorize: 2(x + y)2 − 9(x + y) − 5
Ans. We have: 2(x+y)2-9(x+y)-5
Let:(x+y)=u
Thus, the given expression becomes
2u2-9u-5
Now, we have to split (-9) into two numbers such that their sum is (-9) and their product is (-10).
Clearly, -10+1=-9 and -10×1=-10.
∴2u2-9u-5
=2u2-10u+u-5
=2u(u-5)+1(u-5)
=(u-5)(2u+1)
Putting u=(x+y), we get:
2(x+y)2 - 9(x+y) - 5
= (x+y-5)[2(x+y)+1]
= (x+y-5)(2x+2y+1)
Q.60. Factorize: 9(2a − b)2 − 4(2a − b) − 13
Ans. We have: 9(2a-b)2-4(2a-b)-13
Let:(2a-b)=p
Thus, the given expression becomes
9p2-4p-13
Now, we must split (-4) into two numbers such that their sum is (-4) and their product is (-117).
Clearly, -13+9=-4 and -13×9=-117.
∴ 9p2-4p-13
=9p2+9p-13p-13
=9p(p+1)-13(p+1)
=(p+1)(9p-13)
Putting p=(2a-b), we get: 9(2a-b)2-4(2a-b)-13
=[(2a-b)+1][9(2a-b)-13]
=(2a-b+1)[18a-9b-13]
Q. 61. Factorise: 7(x−2y)2−25(x−2y)+12
Ans. 7(x−2y)2−25(x−2y)+12
=7(x−2y)2−21(x−2y)−4(x−2y)+12
=[7(x−2y)](x−2y−3)−4(x−2y−3)
=[7(x−2y)−4](x−2y−3)
=(7x−14y−4)(x−2y−3)7x-2y2-25x-2y+12
=7x-2y2-21x-2y-4x-2y+12
=7x-2yx-2y-3-4x-2y-3
=7x-2y-4x-2y-3
=7x-14y-4x-2y-3
Hence, factorisation of 7(x−2y)2−25(x−2y)+12 is (7x−14y−4)(x−2y−3)
Q.62. Factorise: 10(3x+1/x)2−(3x+1/x)−3
Ans. 10(3x+1/x)2−(3x+1/x)−3
=10(3x+1/x)2−6(3x+1/x)+5(3x+1/x)−3
=[2(3x+1/x)][5(3x+1/x)−3]+1[5(3x+1/x)−3]
=[5(3x+1/x)−3][2(3x+1/x)+1]
=(15x+5/x−3)(6x+2/x+1)
Hence, factorisation of 10(3x+1/x)2−(3x+1/x)−3 is (15x+5/x−3)(6x+2/x+1)
Q.63. Factorise: 6(2x−3/x)2+7(2x−3/x)−20
Ans. 6(2x−3/x)2+7(2x−3/x)−20
=6(2x−3/x)2+15(2x−3x)−8(2x−3x)−20
=[3(2x−3/x)][2(2x−3/x)+5]−4[2(2x−3/x)+5]
=[2(2x−3/x)+5][3(2x−3/x)−4]
=(4x−6/x+5)(6x−9/x−4)
Hence, factorisation of 6(2x−3/x)2+7(2x−3/x)−20 is (4x−6/x+5)(6x−9/x−4)
Q.64. Factorise: (a+2b)2+101(a+2b)+100
Ans. (a+2b)2+101(a+2b)+100
=(a+2b)2+100(a+2b)+1(a+2b)+100
=(a+2b)[(a+2b)+100]+1[(a+2b)+100]
=[(a+2b)+1][(a+2b)+100]
=(a+2b+1)(a+2b+100)
Hence, factorisation of (a+2b)2+101(a+2b)+100 is (a+2b+1)(a+2b+100)
Q.65. Factorise: 4x4 + 7x2 – 2
Ans. 4x4+7x2−2
=4x4+8x2−x2−2
=4x2(x2+2)−1(x2+2)
=(4x2−1)(x2+2)
Hence, factorisation of 4x4 + 7x2 – 2 is (4x2−1)(x2+2)
Q.66. Evaluate {(999)2 – 1}.
Ans. {(999)2−1}
={(999)2−12}
=(999−1)(999+1)
=(998)(1000)
=998000
Hence, {(999)2 – 1} = 998000.