Playing With Numbers (Exercise 2.8) RD Sharma Solutions | Mathematics (Maths) Class 6 PDF Download
Q.1. Find the largest number which 615 and 963 leaving remainder 6 in each case.
Ans: We have to find the largest number which divides (615 − 6) and (963 − 6) exactly.
Therefore, the required number = HCF of 609 and 957
Resolving 609 and 957 into prime factors, we have:
609 = 3 × 7 × 29
957 = 3 × 11 × 29
Therefore, HCF of 609 and 957 = 29 × 3 = 87
Hence, the required largest number is 87.
Q.2. Find the greatest number which divides 285 and 1249 leaving remainders 9 and 7 respectively.
Ans: We have to find the greatest number which divides (285 − 9) and (1,249 − 7) exactly.
The required number will be given by the HCF of 276 and 1242.
Resolving 276 and 1242 into prime factors, we have:
276 = 2 × 2 × 3 × 23
1242 = 2 × 3 × 3 × 3 × 23
∴ HCF of 276 and 1242 is 2 × 3 × 23 = 138.
Q.3. What is the largest number that divides 626,3127 and 15628 and leaves remainders of 1,2 and 3 respectively?
Ans: We have to find the largest number which divides (626 − 1), (3,127 − 2), and (15,628 − 3) exactly.
The required number will be given by the HCF of 625, 3,125 and 15,625.
Resolving 625, 3125, and 15625 into prime factors, we have:
625 = 5 × 5 × 5 × 5
3,125 = 5 × 5 × 5 × 5 × 5
15,625 = 5 × 5 × 5 × 5 × 5 × 5
Therefore, HCF of 625, 3125 and 15625 = 5 × 5 × 5 × 5 = 625
Hence, the required largest number is 625.
Q.4. The length, breadth and height of a room are 8 m 25 cm, 6 m 75 cm and 4 m 50 cm, respectively. Determine the longest rod which can measure the three dimensions if the room exactly.
Ans: Given:
Length of the room = 8 m 25 cm = 825 cm
Breadth of the room = 6 m 75 cm = 675 cm
Height of the room = 4 m 50 cm = 450 cm
The longest rod will be given by the HCF of 825, 675 and 450.
Prime factorisation of 825 = 3 × 5 × 5 × 11
Prime factorisation of 675 = 3 × 3 × 3 × 5 × 5
Prime factorisation of 450 = 2 × 3 × 3 × 5 × 5
Therefore, HCF of 825, 675 and 450 = 3 × 5 × 5 = 75
Thus, the required length of the longest rod is 75 cm.
Q.5. A rectangular courtyard is 20 m 16 cm long and 15 m 60 cm broad. It is to be paved with square stones of the same size. Find the least possible number of such stones.
Ans:
Length of the rectangular courtyard = 20 m 16 cm = 2,016 cm
Breadth of the rectangular courtyard = 15 m 60 cm = 1,560 cm
Least possible side of the square stones used to pave the rectangular courtyard = HCF of (2,016 and 1,560)
Prime factorisation of 2,016 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 7
Prime factorisation of 1,560 = 2 × 2 × 2 × 3 × 5 × 13
HCF of (2,016, 1,560) = 2 × 2 × 2 × 3 = 24
Least possible side of square stones used to pave the rectangular courtyard is 24 cm.
Number of square stones used to pave the rectangular courtyard
=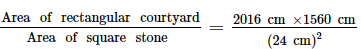 =5460
=5460
Thus, the least number of square stones used to pave the rectangular courtyard is 5,460.
Q.6. Determine the longest tape which can be used to measure exactly the lengths 7 m, 3 m 85 cm and 12 m 95 cm.
Ans: Given:
Length of the first tape = 7 m = 700 cm
Length of the second tape = 3 m 85 cm = 385 cm
Length of the third tape = 12 m 95 cm = 1,295 cm
The length of the longest tape will be the HCF of 700, 385, and 1,295.
Prime factorisation of 700 = 2 × 2 × 5 × 5 × 7
Prime factorisation of 385 = 5 × 7 × 11
Prime factorisation of 1,295 = 5 × 7 × 37
∴ HCF of 700, 385, and 1,295 = 5 × 7 = 35
∴ Required length of the longest tape = 35 cm
Q.7. 105 goats, 140 donkeys and 175 cows have to be taken across a river. There is only one boat which will have to make many trips in order to do so. The lazy boatman has his own conditions for transporting them. He insists that he will take the same number of animals in every trip and they have to be of the same kind. He will naturally like to take the largest possible number each time. Can you tell how many animals went in each trip.
Ans: We have to find the largest possible number of animals. Thus, we will have to find the HCF of 105, 140, and 175.
Prime factorisation of 105 = 3 × 5 × 7
Prime factorisation of 140 = 2 × 2 × 5 × 7
Prime factorisation of 175 = 5 × 5 × 7
∴ Required HCF = 5 × 7 = 35
Hence, 35 animals went in each trip.
Q.8. Two brands of chocolates are available in packs of 24 and 15 respectively. If i need to buy an equal number of chocolates of both kinds, what is the least number of boxes of each kind i would need to buy?
Ans: Let the brand ‘A’ contain 24 chocolates in one packet and brand ‘B’ contain 15 chocolates in one packet.
Equal number of chocolates of each kind can be find out by taking the LCM of the number of chocolates in each packet.
∴ LCM of 15 and 24 is:
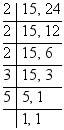
Required LCM = 2 × 2 × 2 × 3 × 5 = 120
Therefore, minimum 120 chocolates of each kind should be purchased.
Number of boxes of brand ‘A’ which needs to be purchased = 120 ÷ 24 = 5
Number of boxes of brand ‘B’ which needs to be purchased = 120 ÷ 15 = 8
Q.9. During a sale, colour pencils were being sold in packs of 24 each and crayons in packs of 32 each. If you want full packs of both and the same number of pencils and crayons, how many each would you need to buy?
Ans: To find the required number of pencils and crayons, we need to find the LCM of 24 and 32.
Prime factorisation of 24 = 2 × 2 × 2 × 3
Prime factorisation of 32 = 2 × 2 × 2 × 2 × 2
∴ Required LCM of 24 and 32 = 2 × 2 × 2 × 2 × 2 × 3 = 96
Thus, number of pencils and crayons needed to be bought is 96 each, i.e. 96÷24=4 packs of colour pencils and 96÷32 = 3 packs of crayons.
Q.10. Reduce each of the following fractions to the lowest terms:
(i)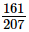
(ii)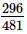
Ans:
(i) For reducing the given fraction to the lowest terms, we have to divide its numerator and denominator by their HCF.
Now, we have to find the HCF of 161 and 207.
Prime factorisation of 161 = 7 × 23
Prime factorisation of 207 = 3 × 3 × 23
∴ HCF of 161 and 207 = 23
Now, 161÷23207÷23=7/9
Hence, 79 is the required fraction.
(ii) For reducing the given fraction to the lowest terms, we have to divide its numerator and denominator by their HCF.
Now, we have to find the HCF of 296 and 481.
Prime factorisation of 296 = 2 × 2 × 2 × 37
Prime factorisation of 481 = 13 × 37
∴ HCF of 296 and 481 = 37
Now, 296 ÷ 37481 ÷ 37 = 8/13
Hence, 813 is the required fraction.
Q.11. A merchant has 120 litres of oil of one kind, 180 liters of another kind and 240 litres of third kind. He wants to sell the oil by filling the three kinds of oil in tins of equal capacity. What should be the greatest capacity of such a tin?
Ans: The maximum capacity of the required tin is the HCF of the three quantities of oil.
Prime factorisation of 120 = 2 × 2 × 2 × 3 × 5
Prime factorisation of 180 = 2 × 2 × 3 × 3 × 5
Prime factorisation of 240 = 2 × 2 × 2 × 2 × 3 × 5
∴ HCF of 120, 180, and 240 = 2 × 2 × 3 × 5 = 60
Hence, the required greatest capacity of the tin must be 60 litres
|
92 videos|348 docs|54 tests
|






















