Stress & Strain
Stress
When a material is subjected to an external force, internal resisting forces develop within the component. The intensity of these internal forces per unit area at a point is called the stress. In common engineering practice the original cross-sectional area is used to calculate stress; this is known as engineering stress or conventional stress.
- The engineering (normal) stress is given by σ = P / A, where P is the axial internal (or external) force and A is the original cross-sectional area.
- P is measured in newton (N) and A in square metre (m2), so stress σ is in N/m2 which is called Pascal (Pa).
- Multiples commonly used in practice:
- 1 kPa = 103 Pa = 103 N/m2
- 1 MPa = 106 Pa = 106 N/m2 = 1 N/mm2
- 1 GPa = 109 Pa = 109 N/m2
Stress- For an axially loaded member the resultant of internal forces on a section cut perpendicular to the member axis is normal to that section; the intensity of this normal internal force is called normal stress.
ITry yourself: What is the unit of stress?
Tensile Stress
If the computed value of σ is positive (σ > 0), the stress is tensile. Under tensile stress the fibres of the component tend to elongate. The distribution of tensile stress over a uniform cross-section is shown in the figure.
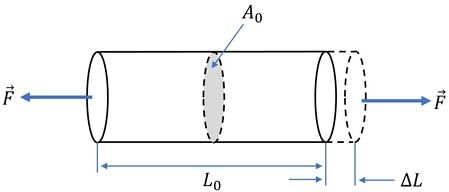Tensile StressCompressive Stress (σc)
- If σ < 0, the stress is compressive and the fibres tend to shorten.
- A member subjected to a compressive axial force P develops compressive stresses across its cross-section as indicated in the figure for such members.
Shear Stress (τ)
- Shear stress acts tangentially (parallel) to the plane of the cross-section under consideration.
- The internal forces that act in the plane of the section are called shearing forces.
- Average shear stress on a plane is given by T = P / A where P is the shear force and A the area resisting that shear.
Strain
Strain is a measure of deformation and is defined as displacement per unit length; it is dimensionless.
- The normal (longitudinal) strain is ε = ΔL / L0, where ΔL is the change in length and L0 the original length.
- Strain is a ratio of two lengths and therefore has no units.
Tensile Strain
- The elongation per unit length under tensile load is called tensile strain.
- εt = ΔL / L0 (engineering or conventional strain - original length used in denominator).
Tensile StrainCompressive Strain
- When the applied load is compressive, the reduction in length per unit length is called compressive strain.
- Compress ive strain is negative in sign when tensile strain is taken as positive.
- εc = -ΔL / L0
Shear Strain (γ)
When tangential forces displace one face of an element relative to the opposite face, the change in right angle between two originally perpendicular lines is called shear strain and is denoted by γ.
If the lateral displacement of the upper face is e and the distance between the faces is L, then the shear strain is approximately
Shear StrainHooke's Law
- Within the elastic limit, normal stress is directly proportional to normal strain and shear stress is directly proportional to shear strain.
- Mathematical form:
- σ = E ε where E is Young's modulus (modulus of elasticity).
- τ = G γ where G is the shear modulus (modulus of rigidity).
- E and G are material properties that measure resistance to elastic deformation.
Volumetric Strain
For three-dimensional bodies, change in volume is expressed by volumetric strain which is the fractional change in volume.
εv = (V - V0) / V0 = ΔV / V0
- Where V is the final volume, V0 the original volume and ΔV the change in volume.
- Volumetric strain is dimensionless.
- For small strains the volumetric strain equals the sum of principal (linear) strains:
- ΔV / V ≈ εx + εy + εz = ε1 + ε2 + ε3
Poisson's Ratio
Poisson's ratio (ν or μ) is the negative ratio of transverse strain to longitudinal strain for a material subjected to uniaxial stress.
Poisson's ratio
- Typical values of Poisson's ratio for engineering materials lie between -1 and 0.5.
- Many common materials have Poisson's ratio between about 0.0 and 0.5. An example: cork has a Poisson's ratio close to zero and is therefore suitable where lateral expansion must be minimised.
Ratios of various materialBiaxial Stretching of a Sheet
When a thin sheet is stretched in two orthogonal in-plane directions, the strains and stresses in the two directions are related by material constants and the boundary conditions. The diagram below illustrates biaxial stretching.
RatioElongation of Bars
Elongation (change in length) depends on the distribution of axial stress and the modulus of elasticity.
Elongation for a bar- Where L is the original length, A the cross-sectional area, and E Young's modulus.
Elongation of Composite Body
For two or more bars of different materials connected in series (loaded axially), the total elongation is the sum of elongations of individual bars:
Elongation of a composite bodyElongation of a Tapered Body
For a bar whose cross-section varies along its length, elongation is obtained by integrating local strain along the length:
Elongation of a tapered bodyElongation of a body due to its Self-weight
A vertical bar under its own weight has a varying axial force along its length; the elongation is found by integrating the incremental elongation produced by the weight of the portion below the section.
Elongation due to self-weightThermal (Temperature) Strain and Stress
- When temperature of a material changes by ΔT, the material undergoes free thermal expansion or contraction. If the deformation is unrestrained, there is strain but no stress.
- The free thermal strain is εthermal = α ΔT, where α is the coefficient of linear thermal expansion of the material.
- If thermal expansion or contraction is restrained, thermal stresses develop. For a completely restrained member the induced thermal stress is σt = α E ΔT.
- An increase in temperature, when restrained, produces a compressive thermal stress. A decrease in temperature, when restrained, produces a tensile thermal stress.
Worked Example
Problem: A steel rod of original length 2.00 m and cross-sectional area 200 mm2 is subjected to an axial tensile force of 50 kN. Take Young's modulus for steel as 200 GPa. Find (a) the engineering tensile stress and (b) the tensile strain.
Sol.
Convert all quantities to SI base units.
Area: 200 mm2 = 200 × 10-6 m2 = 2.00 × 10-4 m2
Force: 50 kN = 50 × 103 N
Young's modulus: E = 200 GPa = 200 × 109 Pa
Compute engineering stress using σ = P / A.
σ = (50 × 103 N) / (2.00 × 10-4 m2)
σ = 2.5 × 108 N/m2 = 250 MPa
Compute tensile strain using Hooke's law ε = σ / E.
ε = (2.5 × 108 Pa) / (200 × 109 Pa)
ε = 1.25 × 10-3
The tensile strain is dimensionless; the elongation ΔL = ε L0 = 1.25 × 10-3 × 2.00 m = 2.50 × 10-3 m = 2.5 mm.
Ans. σ = 250 MPa; ε = 1.25 × 10-3; ΔL = 2.5 mm.
FAQs on Stress & Strain
| 1. What's the difference between stress and strain in strength of materials? |  |
| 2. How do I calculate stress if I know the force and cross-sectional area? | |
| 3. Why do some materials show elastic behaviour while others show plastic deformation? | |
| 4. What does a stress-strain diagram actually tell me about material properties? | |
| 5. Can strain ever be negative, and what does that actually mean? | |
