Mechanical Engineering Exam > Mechanical Engineering Notes > Strength of Materials (SOM) > Euler's Theory of Columns
Euler's Theory of Columns | Strength of Materials (SOM) - Mechanical Engineering PDF Download
Columns and Struts
- A structural member subjected to an axial compressive force is called strut. As per definition strut may be horizontal, inclined or even vertical.
- The vertical strut is called a column.
Euler’s Column Theory
Assumptions of Euler's theory:
Euler's theory is based on the following assumptions:
(i) Axis of the column is perfectly straight when unloaded.
(ii) The line of thrust coincides exactly with the unstrained axis of the column.
(iii) Flexural rigidity El is uniform.
(iv) Material is isotropic and homogeneous.
Limitation of Euler’s Formula
- There is always crookedness in the column and the load may not be exactly axial.
- This formula does not take into account the axial stress and the buckling load is given by this formula may be much more than the actual buckling load.
Euler’s Buckling (or crippling load)
The maximum load at which the column tends to have lateral displacement or tends to buckle is known as buckling or crippling load. Load columns can be analysed with the Euler’s column formulas can be given as
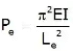
where, E = Modulus of elasticity, Le = Effective Length of column, and I = Moment of inertia of column section.
(i) For both end hinged
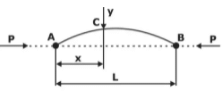in case of Column hinged at both end Le = L
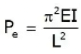
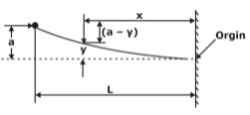
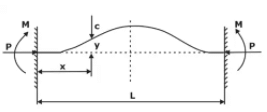
in case of column one end fixed and other free: Le = 2L
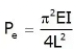
in case of Column with both end Fixed Le = L / 2
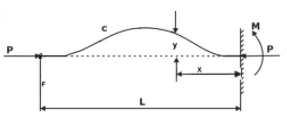in case of Column with one end fixed and other hinged Le = L / √2
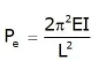
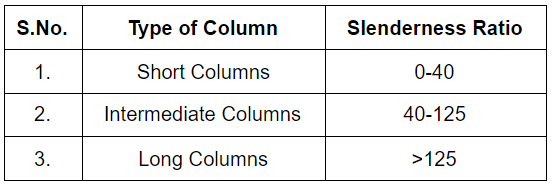
Slenderness Ratio (S)
The slenderness ratio of a compression member is defined as the ratio of its effective length to least radius of gyration.
slenderness (s) = Le / k = Effective length of member / Least radius of gyration
Rankine proposed an empirical formula for columns which coven all Lasts ranging from very short to very long struts. He proposed the relation
1 / PR = 1 / PC + 1 / PE
Pc = σC. A = ultimate load for a strut
Eulerian crippling load for the standard case
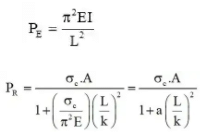
Where a = Rankine's constant = 
The document Euler's Theory of Columns | Strength of Materials (SOM) - Mechanical Engineering is a part of the Mechanical Engineering Course Strength of Materials (SOM).
All you need of Mechanical Engineering at this link: Mechanical Engineering
|
37 videos|102 docs|47 tests
|
FAQs on Euler's Theory of Columns - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is Euler's Theory of Columns in mechanical engineering? |  |
Ans. Euler's Theory of Columns is a concept in mechanical engineering that deals with the stability and strength of slender columns under compressive loads. It provides a mathematical framework to determine the critical load at which a column will buckle or fail.
| 2. What are the assumptions made in Euler's Theory of Columns? | |
Ans. Euler's Theory of Columns makes certain assumptions for its application, including:
- The column is slender and has a constant cross-section along its length.
- The material of the column is homogeneous and isotropic, exhibiting linear-elastic behavior.
- The column is subjected to an axial compressive load without any lateral forces or moments.
- The column buckles in a single plane and does not experience any lateral deflection.
| 3. How is the critical buckling load determined in Euler's Theory of Columns? | |
Ans. The critical buckling load in Euler's Theory of Columns can be determined using the formula:
Pcr = (π^2 * E * I) / (l^2)
Where Pcr is the critical load, E is the modulus of elasticity of the column material, I is the moment of inertia of the column's cross-section, and l is the effective length of the column.
| 4. What is the significance of Euler's Theory of Columns in mechanical engineering? | |
Ans. Euler's Theory of Columns is of great significance in mechanical engineering as it helps engineers design and analyze slender columns to ensure their stability and prevent buckling failures. It provides a fundamental understanding of how loads and geometry affect the behavior of columns under compression, aiding in the safe and efficient design of various structural systems.
| 5. Can Euler's Theory of Columns be applied to all types of columns? | |
Ans. Euler's Theory of Columns is primarily applicable to long, slender columns with relatively low slenderness ratios. It is most accurate for columns with pinned or hinged ends, as well as those with fixed or clamped ends. However, for columns with intermediate slenderness ratios or special boundary conditions, more advanced theories, such as the Rankine-Gordon formula or Perry-Robertson formula, may be required for accurate analysis.
About this Document
4.86/5
Rating
Jul 13, 2025
Last updated
Related Exams
Document Description: Euler's Theory of Columns for Mechanical Engineering 2025 is part of Strength of Materials (SOM) preparation.
The notes and questions for Euler's Theory of Columns have been prepared according to the Mechanical Engineering exam syllabus. Information about Euler's Theory of Columns covers topics
like and Euler's Theory of Columns Example, for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Euler's Theory of Columns.
Introduction of Euler's Theory of Columns in English is available as part of our Strength of Materials (SOM)
for Mechanical Engineering & Euler's Theory of Columns in Hindi for Strength of Materials (SOM) course.
Download more important topics related with notes, lectures and mock test series for Mechanical Engineering
Exam by signing up for free. Mechanical Engineering: Euler's Theory of Columns | Strength of Materials (SOM) - Mechanical Engineering
Description
Full syllabus notes, lecture & questions for Euler's Theory of Columns | Strength of Materials (SOM) - Mechanical Engineering - Mechanical Engineering | Plus excerises question with solution to help you revise complete syllabus for Strength of Materials (SOM) | Best notes, free PDF download
Information about Euler's Theory of Columns
In this doc you can find the meaning of Euler's Theory of Columns defined & explained in the simplest way possible. Besides explaining types of
Euler's Theory of Columns theory, EduRev gives you an ample number of questions to practice Euler's Theory of Columns tests, examples and also practice Mechanical Engineering
tests
Related Searches
past year papers
,Viva Questions
,ppt
,Summary
,shortcuts and tricks
,video lectures
,Semester Notes
,Previous Year Questions with Solutions
,MCQs
,Euler's Theory of Columns | Strength of Materials (SOM) - Mechanical Engineering
,practice quizzes
,Important questions
,Free
,Extra Questions
,Exam
,study material
,Sample Paper
,mock tests for examination
,Euler's Theory of Columns | Strength of Materials (SOM) - Mechanical Engineering
,Objective type Questions
,Euler's Theory of Columns | Strength of Materials (SOM) - Mechanical Engineering
,
Additional Information about Euler's Theory of Columns for Mechanical Engineering Preparation
Euler's Theory of Columns Free PDF Download
The Euler's Theory of Columns is an invaluable resource that delves deep into the core of the Mechanical Engineering exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Euler's Theory of Columns now and kickstart your journey towards success in the Mechanical Engineering exam.
Importance of Euler's Theory of Columns
The importance of Euler's Theory of Columns cannot be overstated, especially for Mechanical Engineering aspirants.
This document holds the key to success in the Mechanical Engineering exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Euler's Theory of Columns Notes
Euler's Theory of Columns Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Euler's Theory of Columns.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Euler's Theory of Columns Notes on EduRev are your ultimate resource for success.
Euler's Theory of Columns Mechanical Engineering Questions
The "Euler's Theory of Columns Mechanical Engineering Questions" guide is a valuable resource for all aspiring students preparing for the
Mechanical Engineering exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Euler's Theory of Columns on the App
Students of Mechanical Engineering can study Euler's Theory of Columns alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Euler's Theory of Columns,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Euler's Theory of Columns is prepared as per the latest Mechanical Engineering syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup