Linear Programming | Industrial Engineering - Mechanical Engineering PDF Download
Linear Programming Problem (LPP)
It is used for the optimization of our limited resources when there is a number of alternate solution possible for the problem.
A Linear Programming Problem (LPP) has three main parameters named as:
- These are the economic or physical quantities, which are competing with one another for sharing the given limited resources.
- In linear programming, these variables must form a linear relationship among them.
- The numerical values of decision variables represent the solution of LPP.
- In a linear programming problem, the objective function forms a linear function of the decision variable expressing the objective of the decision-maker.
- Example: maximization of profit or contribution, minimization of cost/time.
- The constraints put limitations on the resources allocated among various decision variables. The resources may be in the form of production capacity, manpower, time, space or machinery.
- Generally, these are written in linear equations in equal terms (i.e. =) or in inequalities form (i.e. > or < type) in terms of decision variables. Thus, these represent the linear equalities or inequalities arising out of practical limitations.
- Non-negativity Restriction Non-negativity restriction indicates that: All decision variables ≥ 0.
Basic Assumptions or Laws of LPP
- Certainty: All parameters, availability of resources, profit consumption of resources must be fixed.
- Divisibility (or continuity): Non-negative values of decision variable can positive frictional value.
- Proportionality: Decision variable directly proportional to the value of the variable.
- Additivity: The value of the objective function for a given value of decision variables and the total sum of resources used by each decision respectively.
Note: LPP involving two decision variables can easily be solved by the graphical method.
Graphical Method Steps
- Identify the problem, define decision variables, objective function, and constraints.
- Draw a graph including all the constraints and search the common feasible region.
- Find out the point within the feasible region which optimizes the objective fun this point gives the final optimum solution.
- One of the corner points of the feasible region gives the final solution because objective fun is a straight line with a constant slope and as it moves away from the origin there is an increase in its value and the corner extreme point will be its optimum value.
- The objective function will be tangent to that point and give the optimum solution.
Special cases
- Infinite or multi-optimal solution: Infinite solution means we get the same optimum value of the objective function for different varying variables.
- No solution or in-feasibility: In some conditions constraint may in inconsistent in such a manner that it is not possible to find a feasible region where all the constraints are satisfied, it is termed as no solution or in-feasibility.
- Unbounded solution: In some conditions, the highest value of objective function goes up-to infinite and it simply means that the common feasible region is not bounded by the limit on the constraints.
Simplex Method
When the decision variables are more than two, the graphical method becomes inadequate and the linear programming problem is solved by the simplex method. The simplex method is defined as an algebraic procedure that through a series of repetitive operations progressively approaches an optimal solution.
The simplex method is based on 2 fundamental conditions, they are:
- Conditions of Feasibility: It assumes that if the initial solution is basic feasible, and then during computation, only basic feasible solutions will be obtained.
- Condition of Optimality: It ensures that only better solutions will be encountered.
Simplex Procedure
- Setup the objective function.
- Setup the constrained equations.
- Convert the inequalities to equalities.
Special cases
- Unique solution: If the number of basic variables is equal to the number of zeros, then the solution is unique.
- Infinite or multi-optimum solution: When a non-basic variable in an optimum solution has zero value for Δj row then the solution is not unique and it indicates that the problem has infinite no. of solution.
- Unbounded solution: If in a case all the values in the replacement ratio column are either –ve or infinite then the solution terminates and it indicates that the problem has an unbounded solution.
- No-solution/in-feasibility: When in the final solution artificial variable remains in the basis then there is no feasible solution to the problem.
- Degenerate solution: When one or more of the basic variables becomes equal to zero during calculation then the solution is called degenerate & the condition is known as degeneracy. In a degenerate solution the no. of basic variables becomes less than equality constraint.
BIG. M Method
- Big M method is a modified form of simplex method, and it is always used whenever the constraints are of (≥ or =) type irrespective of whether the problem is for maximization or for minimization.
- In this condition, we introduce artificial variables in the current solution to get an initial working matrix.
- These artificial variables must not appear in the final solution and this is ensured by providing an extremely negative value (M) to their profit coefficients in the objection function.
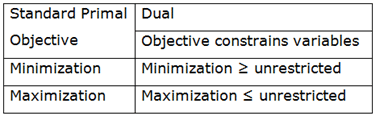
Duality in Linear Programming
Corresponding to a linear programming problem is another linear programming problem formulated from the Parameters of the original problem.
- Dual Theorem of Linear Programming: States a theoretic relationship between the primal and dual problems.
- Dual Variables: These are the variables of the dual LPP.
- Primal Problem: is the original linear programming problem.
- Post-Optimality (Sensitivity) Analysis: AGA linear programming problem is a study of the effect of changes of the profit of resource level on the solution.
|
30 videos|64 docs|30 tests
|
FAQs on Linear Programming - Industrial Engineering - Mechanical Engineering
| 1. What is linear programming and how is it related to mechanical engineering? |  |
| 2. How does the graphical method work in linear programming? |  |
| 3. What are the advantages of using linear programming in mechanical engineering? |  |
| 4. Can linear programming be used to optimize complex mechanical systems? |  |
| 5. Are there any limitations or challenges in applying linear programming to mechanical engineering problems? |  |





















