Deflection of Beams | Solid Mechanics - Mechanical Engineering PDF Download
Deflections of Beam
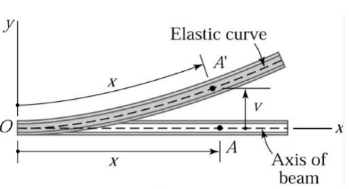
The deformation of a beam is usually expressed in terms of its deflection from its original unloaded position. The deflection is measured from the original neutral surface of the beam to the neutral surface of the deformed beam. The configuration assumed by the deformed neutral surface is known as the elastic curve of the beam.
- Slope of a Beam: Slope of a beam is the angle between deflected beam to the actual beam at the same point.
- Deflection of Beam: Deflection is defined as the vertical displacement of a point on a loaded beam. There are many methods to find out the slope and deflection at a section in a loaded beam.
The maximum deflection occurs where the slope is zero. The position of the maximum deflection is found out by equating the slope equation zero. Then the value of x is substituted in the deflection equation to calculate the maximum deflection
Methods of Determining Beam Deflections
Numerous methods are available for the determination of beam deflections. These methods include:
1. Double Integration Method
- This is most suitable when concentrated or udl over entire length is acting on the beam. A double integration method is a powerful tool in solving deflection and slope of a beam at any point because we will be able to get the equation of the elastic curve.

- In the derivation of flexure formula, the radius of curvature of a beam is
ρ = EI / M - Deflection of beams is so small, such that the slope of the elastic curve dy/dx is very small, and squaring this expression the value becomes practically negligible, hence
ρ = 1 / d2y / dx2 = 1 / y"
Thus, EI / M = 1 / y"
y" = M / EI = (1 / EI)M - If EI is constant, the equation may be written as:
EIy′′ = M
where x and y are the coordinates shown in the figure of the elastic curve of the beam under load,
- y is the deflection of the beam at any distance x.
- E is the modulus of elasticity of the beam,
- I represent the moment of inertia about the neutral axis, and
- M represents the bending moment at a distance x from the end of the beam.
The product EI is called the flexural rigidity of the beam.
(EI)(d2y / dx2) = -M
Integrating one time
EI(dy / dx) = -∫M
The first integration y'(dy / dx) yields the Slope of the Elastic Curve
Second Integration
EIy = -∫∫M
The second integration y gives the Deflection of the Beam at any distance x.
- The resulting solution must contain two constants of integration since EI y" = M is of second order. These two constants must be evaluated from known boundary conditions concerning the slope deflection at certain points of the beam.
- For instance, in the case of a simply supported beam with rigid supports, at x = 0 and x = L, the deflection y = 0, and in locating the point of maximum deflection, we simply set the slope of the elastic curve y' to zero
2. Area Moment Method
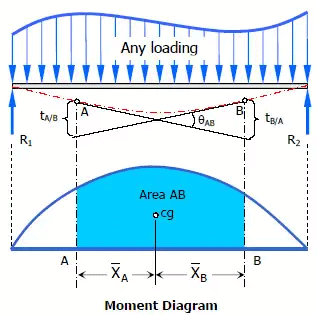
- Another method of determining the slopes and deflections in beams is the area-moment method, which involves the area of the moment diagram.
- The moment-area method is a semi graphical procedure that utilizes the properties of the area under the bending moment diagram. It is the quickest way to compute the deflection at a specific location if the bending moment diagram has a simple shape.

(i) Theorems of Area-Moment Method
- Theorem 1
The change in slope between the tangents drawn to the elastic curve at any two points A and B is equal to the product of 1 / EI multiplied by the area of the moment diagram between these two points
θAB = (1 / EI)(Area between A and B) - Theorem 2
The deviation of any point B relative to the tangent drawn to the elastic curve at any other point A, in a direction perpendicular to the original position of the beam, is equal to the product of 1 / EI multiplied by the moment of an area about B of that part of the moment diagram between points A and B.
tB/A = (1 / EI)(Area between A and B)⋅X¯B
and
tA/B = (1 / EI)(Area between A and B)⋅X¯A
3. Method of Superposition
The method of superposition, in which the applied loading is represented as a series of simple loads for which deflection formulas are available. Then the desired deflection is computed by adding the contributions of the component loads(principle of superposition).
- Mostly direct formula is used in questions, hence it is advised to look for the beam deflection formula which are directly asked from this topic rather than going for long derivations.
Deflection for Common Loadings
1. Concentrated load at the free end of cantilever beam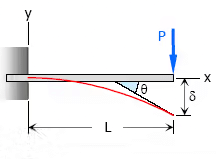
- Maximum Moment, M = −PL
- Slope at end, θ = PL2 / 2EI
- Maximum deflection, δ = PL3 / 3EI
- Deflection Equation (y is positive downward), EIy = (Px2)(3L − x) / 6
2. Concentrated load at any point on the span of the cantilever beam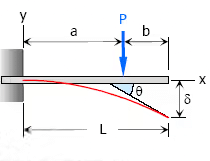
- Maximum Moment. M = -Pa
- Slope at end, θ = Pa2 / 2EI
- Maximum deflection, δ = Pa3(3L − a) / 6EI
- Deflection Equation (y is positive downward),
(i) EIy = Px2(3a − x) / 6 for 0 < x < a
(ii) EIy = Pa2(3x − a) / 6 for a < x < L
3. Uniformly distributed load over the entire length of the cantilever beam
- Maximum Moment, M = −woL2 / 2
- Slope at end, θ = woL3 / 6EI
- Maximum deflection, δ = woL4 / 8EI
- Deflection Equation (y is positive downward), EIy = wox2(6L2 − 4Lx + x2) / 120L
4. Triangular load, full at the fixed end and zero at the free end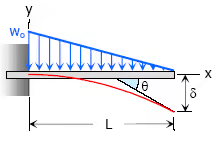
- Maximum Moment, M = −woL2/ 6M
- Slope at end, θ = woL3 / 24EI
- Maximum deflection, δ = woL4 / 30EI
- Deflection Equation (y is positive downward), EIy = wox2(10L3− 10L2x + 5Lx2 − x3) / 120L
5. Moment load at the free end of the cantilever beam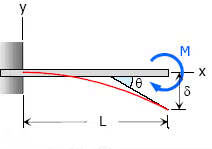
- Maximum Moment, M = −M
- Slope at end, θ = ML / EI
- Maximum deflection, δ = ML2 / 2EI
- Deflection Equation (y is positive downward), EIy = Mx2 / 2
6. Concentrated load at the midspan of simple beam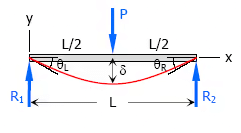
- Maximum Moment, M = PL / 4
- Slope at end, θL = θR = PL2 / 16EI
- Maximum deflection, δ = PL3 / 48EI
- Deflection Equation (y is positive downward), EIy = Px{(3 / 4)L2 − x2)} / 12 for 0 < x < 12L
7. Uniformly distributed load over the entire span of simple beam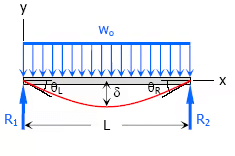
- Maximum Moment, M = woL2 / 8
- Slope at end, θL = θR = woL3 / 24EI
- Maximum deflection, δ = 5woL4 / 384EI
- Deflection Equation (y is positive downward), EIy = wox(L3 − 2Lx2 + x3) / 24
8. Triangle load with zero at one support and full at the other support of simple beam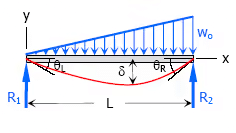
- Maximum Moment, M = woL2 / 9√3
- Slope at end,
(i) θL = 7woL3 / 360EI
(ii) θR = 8woL3 / 360EI - Maximum deflection, δ = 2.5woL4 / 384EI at x = 0.519L
- Deflection Equation (y is positive downward), EIy = wox(7L4 − 10L2x + 3x) / 360L
9. Triangular load with zero at each support and full at the midspan of simple beam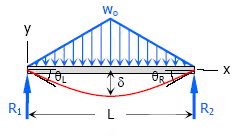
- Maximum Moment, M = woL2 / 12
- Slope at end, θL = θR = 5woL3 / 192EI
- Maximum deflection, δ = w0L4 / 120EI
- Deflection Equation (y is positive downward), EIy = wox(25L4 − 40L2x2 + 16x4) / 960L for 0 < x < L / 2
Beam Deflection Formula
- Cantilever Beams:

- Simply supported Beams:

|
33 videos|27 docs|29 tests
|
FAQs on Deflection of Beams - Solid Mechanics - Mechanical Engineering
| 1. What is beam deflection and why is it important? |  |
| 2. How is beam deflection calculated? |  |
| 3. What factors affect the deflection of a beam? |  |
| 4. How can beam deflection be minimized? |  |
| 5. What are the limitations of beam deflection calculations? |  |

|
Explore Courses for Mechanical Engineering exam
|

|