Recursion | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Understanding Recursion
Recursion refers to the process where a function calls itself, either directly or indirectly, and the function involved in this process is known as a recursive function. By employing a recursive algorithm, certain problems can be tackled with greater ease. Examples of such problems include the Towers of Hanoi, various tree traversal methods (Inorder, Preorder, Postorder), and Depth First Search (DFS) in graphs.
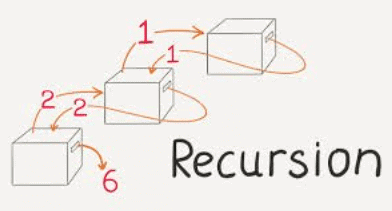
A Mathematical Perspective
To illustrate the concept of recursion, let’s consider the task of calculating the sum of the first n natural numbers. While there are multiple methods to achieve this, the most straightforward approach involves adding the numbers sequentially from 1 to n. This can be represented as:
Approach 1: Iterative Addition
f(n) = 1 + 2 + 3 + ... + n
However, there is a recursive way to express this:
Approach 2: Recursive Addition
f(n) = 1 n=1
f(n) = n + f(n-1) n>1
The key difference between these two approaches is that in Approach 2, the function f(n) calls itself within its definition. This self-referential process is what defines recursion, and functions that utilize this technique are called recursive functions. Recursion is a powerful tool for programmers, enabling them to solve problems in a more straightforward and efficient manner.
What is the Base Condition in Recursion?
In a recursive program, the base condition is crucial as it defines the simplest instance of the problem that can be solved directly. The solution to the base case is provided explicitly, and the solution to larger instances of the problem is expressed in terms of smaller instances.
For example, consider the factorial function:
int fact(int n)
{
if (n <= 1) // base case
return 1;
else
return n*fact(n-1);
}
In the above example, base case for n < = 1 is defined and larger value of number can be solved by converting to smaller one till base case is reached.
How is a Problem Solved Using Recursion?
- Recursion involves breaking down a problem into one or more smaller sub-problems and defining base conditions to stop the recursive calls.
- For instance, to compute the factorial of n, we need to know the factorial of (n-1). The base case for factorial is when n = 0, where we return 1.
Reasons for Stack Overflow Error in Recursion
A stack overflow error in recursion occurs when the base case is either not defined or not reached. The base case is crucial as it determines when the recursive calls should stop. Let’s consider an example to illustrate this:
Let us take an example to understand this.
int fact(int n)
{
if (n == 100) // wrong base case as it will cause stack overflow
return 1;
else
return n*fact(n-1);
}
In this example, if we call fact(10), the function will keep calling itself with decreasing values of n. fact(9), fact(8), fact(7), and so on) . However, the base case is set to n == 100, which will never be reached. This leads to an infinite series of function calls, consuming stack memory. Eventually, this exhausts the available memory on the stack, resulting in a stack overflow error.
Difference Between Direct and Indirect Recursion
When a function calls itself directly, it is known as direct recursion. For example:
// An example of direct recursion
void directRecFun()
{
// Some code....
directRecFun();
// Some code...
}
// An example of indirect recursion
void indirectRecFun1()
{ // Some code...
indirectRecFun2();
// Some code...
}
void indirectRecFun2()
{
// Some code...
indirectRecFun1();
// Some code...
}
Types of Recursion
There are two types of recursion: Tailed Recursion and Non-Tailed Recursion.
- Tailed Recursion: In this type, the recursive call is the last operation performed by the function. The result of the recursive call is returned directly.
- Non-Tailed Recursion: Here, the recursive call is not the last operation. The function performs additional operations after the recursive call, which means it needs to keep track of the state after the call.
Memory Allocation in Recursion
- When a function is called from the main() function, memory is allocated to it on the stack.
- In the case of a recursive function calling itself, memory for the called function is allocated on top of the memory allocated to the calling function. A separate copy of the local variables is created for each function call.
- When the base case is reached, the function returns its value to the calling function, and the memory is de-allocated. This process continues for each level of the recursive calls.
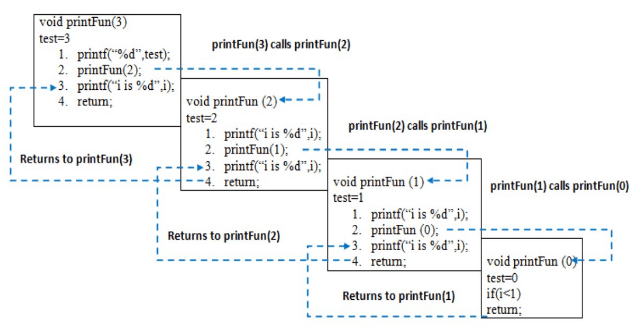
Example of Recursion:
CPP
// A C++ program to demonstrate working of
// recursion
#include <bits/stdc++.h>
using namespace std;
void printFun(int test)
{
if (test < 1)
return;
else {
cout << test << " ";
printFun(test - 1); // statement 2
cout << test << " ";
return;
}
}
// Driver Code
int main()
{
int test = 3;
printFun(test);
}
Java
// A Java program to demonstrate working of
// recursion
class EDU {
static void printFun(int test)
{
if (test < 1)
return;
else {
System.out.printf("%d ", test);
printFun(test - 1); // statement 2
System.out.printf("%d ", test);
return;
}
}
// Driver Code
public static void main(String[] args)
{
int test = 3;
printFun(test);
}
}
Python3
# A Python 3 program to
# demonstrate working of
# recursion
def printFun(test):
if (test < 1):
return
else:
print(test, end=" ")
printFun(test-1) # statement 2
print(test, end=" ")
return
# Driver Code
test = 3
printFun(test)
}
Example Output:
3 2 1 1 2 3
Explanation:
- When printFun(3) is called, memory is allocated to printFun(3), and the local variable test is initialized to 3.
- The function first prints ‘3’ and then calls printFun(2). This process continues until printFun(0) is reached, which triggers the base case.
- As the recursive calls return, the remaining statements are executed, printing the values in reverse order.
Now, let’s discuss a few practical problems which can be solved by using recursion and understand its basic working.
Problem 1: Fibonacci Series
Given n (where n > 2), the task is to write a program and recurrence relation to find the Fibonacci series.
- Mathematical Equation:
n if n == 0, n == 1;
fib(n) = fib(n-1) + fib(n-2) otherwise; - Recurrence Relation:
T(n) = T(n-1) + T(n-2) + O(1)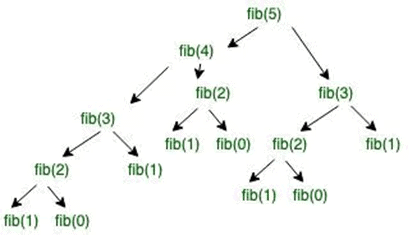
- Recursive Program:
C++
// C++ code to implement Fibonacci series
#include <bits/stdc++.h>
using namespace std;
// Function for fibonacci
int fib(int n)
{
// Stop condition
if (n == 0)
return 0;
// Stop condition
if (n == 1 || n == 2)
return 1;
// Recursion function
else
return (fib(n - 1) + fib(n - 2));
}
// Driver Code
int main()
{
// Initialize variable n.
int n = 5;
cout<<"Fibonacci series of 5 numbers is: ";
// for loop to print the fiboancci series.
for (int i = 0; i < n; i++)
{
cout<<fib(i)<<" ";
}
return 0;
}
Java
// Java code to implement Fibonacci series
import java.util.*;
class EDU
{
// Function for fibonacci
static int fib(int n)
{
// Stop condition
if (n == 0)
return 0;
// Stop condition
if (n == 1 || n == 2)
return 1;
// Recursion function
else
return (fib(n - 1) + fib(n - 2));
}
// Driver Code
public static void main(String []args)
{
// Initialize variable n.
int n = 5;
System.out.print("Fibonacci series of 5 numbers is: ");
// for loop to print the fiboancci series.
for (int i = 0; i < n; i++)
{
System.out.print(fib(i)+" ");
}
}
}
Python3
# Python code to implement Fibonacci series
# Function for fibonacci
def fib(n):
# Stop condition
if (n == 0):
return 0
# Stop condition
if (n == 1 or n == 2):
return 1
# Recursion function
else:
return (fib(n - 1) + fib(n - 2))
# Driver Code
# Initialize variable n.
n = 5;
print("Fibonacci series of 5 numbers is :",end=" ")
# for loop to print the fiboancci series.
for i in range(0,n):
print(fib(i),end=" ")
Output
Fibonacci series of 5 numbers is: 0 1 1 2 3
Time Complexity
- The time complexity of the given program is exponential, specifically O(2n) in the worst case. This is because the function makes two recursive calls for each non-base case, leading to a binary tree of calls.
- In the best case, when the input is very small, the time complexity can be considered O(1) because the function will hit the base cases immediately.
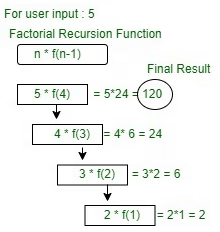
Problem 2: Factorial of n
Write a program and recurrence relation to find the Factorial of n where n>2 .
Mathematical Equation:
1 if n == 0 or n == 1;
f(n) = n * f(n-1) if n> 1;
Recurrence Relation:
T(n) = 1 for n = 0
T(n) = 1 + T(n-1) for n > 0
C++ Implementation
// C++ code to implement factorial
#include <bits/stdc++.h>
using namespace std;
// Factorial function
int f(int n)
{
// Stop condition
if (n == 0 || n == 1)
return 1;
// Recursive condition
else
return n * f(n - 1);
}
// Driver code
int main()
{
int n = 5;
cout<<"factorial of "<<n<<" is: "<<f(n);
return 0;
}
Java Implementation
// Java code to implement factorial
public class EDU
{
// Factorial function
static int f(int n)
{
// Stop condition
if (n == 0 || n == 1)
return 1;
// Recursive condition
else
return n * f(n - 1);
}
// Driver code
public static void main(String[] args)
{
int n = 5;
System.out.println("factorial of " + n + " is: " + f(n));
}
}
Python3
# Python3 code to implement factorial
# Factorial function
def f(n):
# Stop condition
if (n == 0 or n == 1):
return 1;
# Recursive condition
else:
return n * f(n - 1);
# Driver code
if __name__=='__main__':
n = 5;
print("factorial of",n,"is:",f(n))
Output for All Implementations
factorial of 5 is: 120
Time Complexity
- The time complexity for all implementations is O(n), where n is the input number for which the factorial is to be calculated.
- This is because the function makes a recursive call for each number from n down to 1, leading to n recursive calls in total.
Disadvantages of Recursive Programming
- Problem-Solving Power: Both recursive and iterative programs have the same problem-solving capabilities. Every recursive program can be written iteratively and vice versa.
- Space Requirements: Recursive programs have greater space requirements than iterative ones. In recursion, all function calls remain in the stack until the base case is reached, which consumes more memory.
- Time Requirements: Recursive programs generally take more time due to the overhead of function calls and returns. Each function call in recursion adds to the time taken to execute the program.
Advantages of Recursive Programming
- Code Simplicity: Recursion offers a clean and straightforward way to write code. It can make the code easier to understand and maintain.
- Inherent Recursiveness: Some problems are inherently recursive, such as tree traversals and the Tower of Hanoi. For these types of problems, writing recursive code is preferred because it aligns with the nature of the problem.
- Avoiding Manual Stack Management: While it is possible to write iterative solutions for inherently recursive problems using a stack data structure (e.g., Inorder Tree Traversal without Recursion, Iterative Tower of Hanoi), it requires manual management of the stack. Recursion handles the stack automatically, making the code simpler.
|
158 docs|30 tests
|
FAQs on Recursion - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is recursion in computer programming? |  |
| 2. How does recursion work in programming? |  |
| 3. What are the advantages of using recursion in programming? |  |
| 4. What are the limitations of recursion in programming? |  |
| 5. Are there any alternatives to using recursion in programming? |  |






















