Introduction to Matrices | Engineering Mathematics - Engineering Mathematics PDF Download
| Table of contents |

|
| What is a Matrix? |

|
| Types of Matrices |

|
| Adjoint of a Square Matrix |

|
| Inverse of a Square Matrix |

|
| Trace of a matrix |

|
| Solved Examples |

|
What is a Matrix?
A matrix represents a collection of numbers arranged in an order of rows and columns. It is necessary to enclose the elements of a matrix in parentheses or brackets.
A matrix with 9 elements is shown below. This Matrix [M] has 3 rows and 3 columns. Each element of matrix [M] can be referred to by its row and column number. For example, a23 = 6
This Matrix [M] has 3 rows and 3 columns. Each element of matrix [M] can be referred to by its row and column number. For example, a23 = 6
Order of a Matrix
The order of a matrix is defined in terms of its number of rows and columns.
Order of a matrix = No. of rows × No. of columns
Therefore Matrix [M] is a matrix of order 3 × 3.
Transpose of a Matrix
The transpose [M]T of an m x n matrix [M] is the n x m matrix obtained by interchanging the rows and columns of [M].
if A = [aij] mxn , then AT = [bij] nxm where bij = aji
Properties of transpose of a matrix
- (AT)T = A
- (A + B)T = AT + BT
- (AB)T = BTAT
Singular and Nonsingular Matrix
- Singular Matrix: A square matrix is said to be a singular matrix if its determinant is zero i.e. |A| = 0
- Nonsingular Matrix: A square matrix is said to be a non-singular matrix if its determinant is non-zero.
Matrix Addition and Multiplication: Properties
- Commutative Property of Addition: For any two matrices A and B of the same order, their sum is independent of the order in which they are added. Mathematically, A + B = B + A.
- Associative Property of Addition: When three matrices A, B, and C are added, the way in which they are grouped does not affect the sum. This means that (A + B) + C = A + (B + C).
- Non-Commutative Property of Multiplication: For most matrices, the product of A and B is not the same as the product of B and A. In other words, AB ≠ BA in general.
- Associative Property of Multiplication: When multiplying three matrices A, B, and C, the way in which they are grouped does not affect the product. This means that (AB)C = A(BC).
- Distributive Property: Matrix multiplication distributes over addition. This means that if A is multiplied by the sum of B and C, it is the same as multiplying A by B and then by C separately. Mathematically, A(B + C) = AB + AC.
Types of Matrices
1. Square Matrix:. matrix is called a square matrix if it has the same number of rows and columns. For example, a 3x3 matrix is square because it has 3 rows and 3 columns.
2. Symmetric Matrix:. square matrix is symmetric if its transpose is equal to the original matrix. In other words, if A is the matrix, then AT = A. This means that the elements are mirrored along the diagonal.
3. Skew-Symmetric Matrix:. skew-symmetric matrix is a square matrix whose transpose is equal to its negative. This can be represented as AT = -A. This means that the elements are also mirrored along the diagonal, but with opposite signs.
4. Diagonal Matrix:. diagonal matrix is a square matrix where all the non-diagonal entries are zero. This means that only the elements on the diagonal can be non-zero. For example, in a 3x3 diagonal matrix, A11, A22, and A33 can be non-zero, but A12, A13, A21, A23, A31, and A32 must be zero.
5. Identity Matrix: An identity matrix is a special type of square matrix where all the diagonal elements are ones and all other elements are zeros. It is denoted as I. For example, in a 3x3 identity matrix, the elements I11, I22, and I33 are 1, and all other elements are 0.
6. Orthogonal Matrix:. matrix is orthogonal if the product of the matrix and its transpose is equal to the identity matrix. This can be represented as AAT = ATA = I. This means that the rows and columns of the matrix are orthogonal unit vectors.
7. Idempotent Matrix:. matrix is idempotent if when it is multiplied by itself, it gives the same matrix. This can be represented as A2 = A. For example, if A is a 2x2 matrix, and A2 = A, then A is idempotent.
8. Involutory Matrix:. matrix is involutary if when it is multiplied by itself, it gives the identity matrix. This can be represented as A2 = I. This means that the matrix is its own inverse.
Note: It is important to note that every square matrix can be uniquely expressed as the sum of a symmetric matrix and a skew-symmetric matrix. This can be represented as A = 1/2 (AT + A) + 1/2 (A – AT). This means that any square matrix can be decomposed into two parts: one that is symmetric and one that is skew-symmetric.
Adjoint of a Square Matrix
The adjoint of a matrix A is the transpose of the cofactor matrix of A
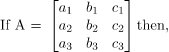

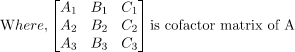
Properties of Adjoint
- A(Adj A) = (Adj A) A = |A| In
- Adj(AB) = (Adj B). (Adj A)
- |Adj A| = |A|n - 1
- Adj(kA) = kn - 1 Adj(A)
- |adj(adj(A))| = |A|^(n - 1)^2
- adj(adj(A)) = |A|^(n - 2) * A
- If A = [L, M, N] then adj(A) = [MN, LN, LM]
- adj(I) = I
Where, “n = number of rows = number of columns”
Inverse of a Square Matrix
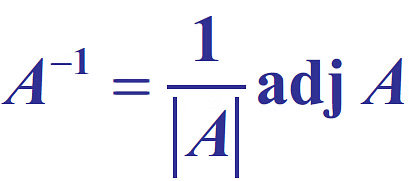 The inverse of a Square Matrix
The inverse of a Square Matrix
Here |A| should not be equal to zero, which means matrix A should be non-singular.
Properties of Inverse
- (A-1)-1 = A
- (AB)-1 = B-1A-1
- Only a non-singular square matrix can have an inverse.
Where should we use the inverse matrix?
If you have a set of simultaneous equations:
7x + 2y + z = 21
3y – z = 5
-3x + 4y – 2x = -1
As we know when AX = B, then X = A-1B so we calculate the inverse of A and by multiplying it B, we can get the values of x, y, and z.
Trace of a matrix
The Trace of a matrix is denoted as tr(A) which is used only for square matrix and equals the sum of the diagonal elements of the matrix. Remember trace of a matrix is also equal to the sum of eigen value of the matrix.
For example:
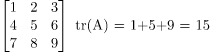
Solved Examples
Q1: For matrices of the same dimension M, N, and scalar c, which one of these properties DOES NOT ALWAYS hold?
(a) (MT)T = M
(b) (cM)T = c(M)T
(c) (M + N)T = MT + NT
(d) MN = NM
Ans: (d)
Sol: Let us consider two 2 × 2 Matrices (same dimension) as shown: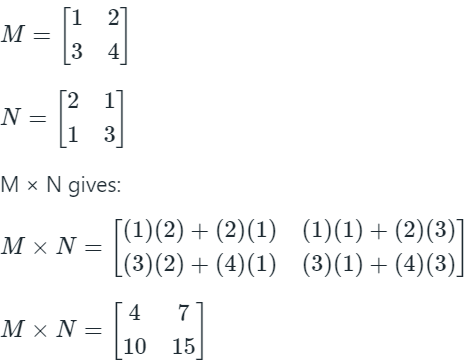
Similarly, N × M gives: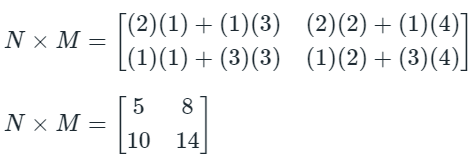
We observe that (M × N)2×2 ≠ (N × M)2×2, even if the dimensions of the two matrices are equal.
But if we take two 2 × 2 Identity Matrices (same dimension), the product will be commutative, i.e. if: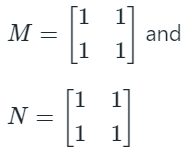
(M × N)2×2 = (N × M)2×2
We, therefore, conclude that (M × N)2×2 IS NOT ALWAYS EQUAL TO (N × M)2×2
Q2: For A = 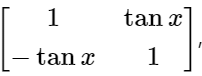 the determinant of ATA-1 is:
the determinant of ATA-1 is:
(a) sec2 x
(b) cos 4x
(c) 1
(d) 0
Ans: (c)
Sol: 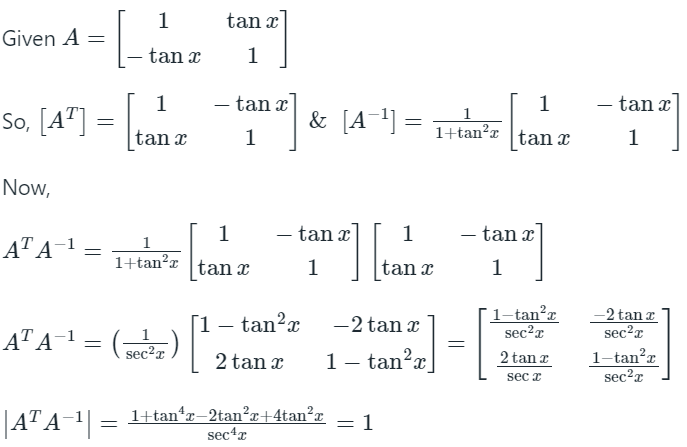
Q3: Let X be a square matrix. Consider the following two statements on X.
I. X is invertible.
II. Determinant of X is non-zero.
Which one of the following is TRUE?
(a) I implies II; II does not imply I.
(b) II implies I; I does not imply II.
(c) I does not imply II; II does not imply I.
(d) I and II are equivalent statements.
Ans: (d)
Sol: I implies II means ≡ I → II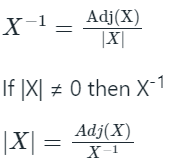
If X-1 then |X| ≠ 0 also |Adj X| = |X|n - 1 then |Adj X| ≠ 0
If X-1 then |X| ≠ 0
I implies II and II implies I
∴ Both I and II are equivalent
Q4: The matrix P is the inverse of a matrix Q. If I denotes the identity matrix, which one of the following options is correct?
(a) PQ = I but QP ≠ I
(b) QP = I but PQ ≠ I
(c) PQ = I and QP = I
(d) PQ – QP = I
Ans: (c)
Sol: Given, P = Q-1
Post multiply by Q
PQ = Q-1Q (we know Q-1Q = I)
PQ = I
Similary, pre-multiply by Q
QP = QQ-1
QP = I (QQ-1 = I)
So, PQ = I and QP = I
|
65 videos|129 docs|94 tests
|
FAQs on Introduction to Matrices - Engineering Mathematics - Engineering Mathematics
| 1. What is a Matrix? |  |
| 2. What are the types of Matrices? |  |
| 3. What is the Adjoint of a Square Matrix? |  |
| 4. How do you find the Inverse of a Square Matrix? |  |
| 5. What is the Trace of a matrix? |  |





















