Rank of Matrix | Engineering Mathematics - Engineering Mathematics PDF Download
The Rank of a Matrix
You can think of an r x c matrix as a set of r row vectors, each having c elements; or you can think of it as a set of c column vectors, each having r elements.
The rank of a matrix is defined as (a) the maximum number of linearly independent column vectors in the matrix or (b) the maximum number of linearly independent row vectors in the matrix. Both definitions are equivalent.
For an r x c matrix,
- If r is less than c, then the maximum rank of the matrix is r.
- If r is greater than c, then the maximum rank of the matrix is c.
The rank of a matrix would be zero only if the matrix had no elements. If a matrix had even one element, its minimum rank would be one.
How to Find Matrix Rank
In this section, we describe a method for finding the rank of any matrix. This method assumes familiarity with echelon matrices and echelon transformations.
The maximum number of linearly independent vectors in a matrix is equal to the number of non-zero rows in its row echelon matrix. Therefore, to find the rank of a matrix, we simply transform the matrix to its row echelon form and count the number of non-zero rows.
Consider matrix A and its row echelon matrix, Aref. Previously, we showed how to find the row echelon form for matrix A.

Because the row echelon form Aref has two non-zero rows, we know that matrix A has two independent row vectors; and we know that the rank of matrix A is 2.
You can verify that this is correct. Row 1 and Row 2 of matrix A are linearly independent. However, Row 3 is a linear combination of Rows 1 and 2. Specifically, Row 3 = 3*( Row 1 ) + 2*( Row 2). Therefore, matrix A has only two independent row vectors.
Full Rank Matrices
When all of the vectors in a matrix are linearly independent, the matrix is said to be full rank. Consider the matrices A and B below.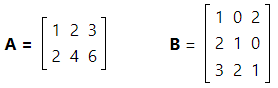
Notice that row 2 of matrix A is a scalar multiple of row 1; that is, row 2 is equal to twice row 1. Therefore, rows 1 and 2 are linearly dependent. Matrix A has only one linearly independent row, so its rank is 1. Hence, matrix A is not full rank.
Now, look at matrix B. All of its rows are linearly independent, so the rank of matrix B is 3. Matrix B is full rank.
|
65 videos|129 docs|94 tests
|
FAQs on Rank of Matrix - Engineering Mathematics - Engineering Mathematics
| 1. What is the rank of a matrix? |  |
| 2. How is the rank of a matrix calculated? |  |
| 3. How does the rank of a matrix relate to its invertibility? |  |
| 4. Can the rank of a matrix be greater than its dimensions? |  |
| 5. How can the rank of a matrix be used in solving systems of linear equations? |  |
















