Quantum Mechanical Model of Atom | Chemistry Class 11 - NEET PDF Download
Need for Quantum Mechanics
Classical mechanics, based on Newton's laws, is great for explaining the motion of large objects like falling stones and planets. However, it falls short when it comes to understanding the movement of really small things such as electrons, atoms, and molecules. Here's why:
- Classical mechanics doesn't consider that tiny particles can behave as both waves and particles.
- There's a level of uncertainty involved in the behavior of these small particles.
To tackle these challenges, scientists turn to a different branch of science called Quantum Mechanics:
- Quantum mechanics explores how tiny things, like atoms and particles, move.
- These tiny objects sometimes act like waves and sometimes like particles.
- Quantum mechanics provides rules for understanding their motion.
- Interestingly, when quantum mechanics is applied to larger objects where wave-like features aren't crucial, the results align with what classical mechanics predicts.
Quantum mechanics was independently developed in 1926 by two scientists, Werner Heisenberg and Erwin Schrödinger.
 Quick Guide to Quantum Mechanics
Quick Guide to Quantum Mechanics
Features of Quantum Mechanical Model of Atom
The quantum mechanical model of an atom gives us a way to understand its structure. It's based on the Schrödinger equation. Here are the important features in simpler terms:
- Quantized Energy:
Electrons in atoms can only have specific energy values, a concept known as quantization. This happens when electrons are bound to the atom's nucleus. - Electronic Energy Levels:
The existence of specific electronic energy levels comes from the wave-like properties of electrons, as determined by the solutions of the Schrödinger wave equation. - Uncertainty in Position and Velocity:
It's impossible to accurately know both the exact position and velocity of an electron in an atom simultaneously, according to the Heisenberg uncertainty principle. We can only talk about the probability of finding an electron at different points. - Atomic Orbitals:
An atomic orbital is like a home for an electron. Each orbital has a definite energy and can hold, at most, two electrons. In multi-electron atoms, electrons fill various orbitals in order of increasing energy. The information about an electron is stored in its orbital wave function ψ, and quantum mechanics helps extract this information. - Probability Density:
The probability of finding an electron at a point within an atom is related to the square of the orbital wave function, denoted as |ψ|². This is called probability density, always positive. By analyzing |ψ|² at different points, we can predict where an electron will most likely be found around the nucleus.
Schrodinger Wave Equation
- Schrodinger wave equation or just Schrodinger equation is one of the most fundamental equations of quantum physics and an important topic for JEE.
- The equation also called the Schrodinger equation is a differential equation and is widely used in Chemistry and Physics to solve problems based on the atomic structure of matter.
- Schrodinger wave equation describes the behavior of a particle in a field of force or the change of a physical quantity over time. Erwin Schrödinger who developed the equation was even awarded the Nobel Prize in 1933.
What is the Schrödinger Wave Equation?
Schrödinger wave equation is a mathematical expression describing the energy and position of the electron in space and time, taking into account the matter wave nature of the electron inside an atom. It is based on three considerations. They are;
- Classical plane wave equation,
- Broglie’s Hypothesis of matter-wave, and
- Conservation of Energy.
Schrödinger equation gives us a detailed account of the form of the wave functions or probability waves that control the motion of some smaller particles.
The equation also describes how these waves are influenced by external factors. Moreover, the equation makes use of the energy conservation concept that offers details about the behavior of an electron that is attached to the nucleus.
Besides, by calculating the Schrödinger equation we obtain Ψ and Ψ2, which helps us determine the quantum numbers as well as the orientations and the shape of orbitals where electrons are found in a molecule or an atom.
There are two equations, which are a time-dependent Schrödinger equation and a time-independent Schrödinger equation. Time-dependent Schrödinger equation is represented as;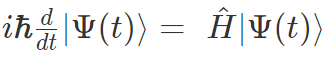
OR
Time-dependent Schrödinger equation in position basis is given as;
Where,
i = imaginary unit, Ψ = time-dependent wavefunction, h2 is h-bar, V(x) = potential and 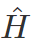 = Hamiltonian operator.
= Hamiltonian operator.
Time-independent Schrödinger equation in compressed form can be expressed as;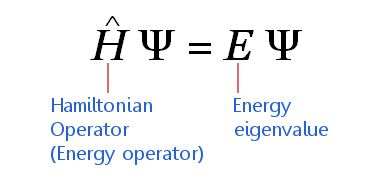
OR
Time-independent-Schrödinger-nonrelativistic-equation
Schrödinger Wave Equation Derivation
Classical Plane Wave Equation
A wave is a disturbance of a physical quantity undergoing simple harmonic motion or oscillations about its place. The disturbance gets passed on to its neighbours in a sinusoidal form.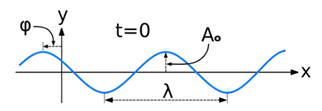
The equation for the wave is a second-order partial differential equation of a scalar variable in terms of one or more space variable and time variable. The one-dimensional wave equation is-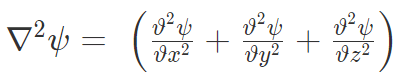
The amplitude (y) for example of a plane progressive sinusoidal wave is given by: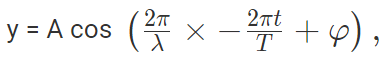
where, A is the maximum amplitude, T is the period and φ is the phase difference of the wave if any and t is the time in seconds. For a standing wave, there is no phase difference, so that,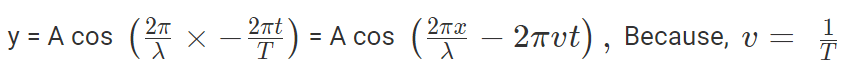
In general the same equation can be written in the form of,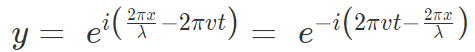
Broglie’s Hypothesis of Matter Wave
Planck’s quantum theory, states the energy of waves are quantized such that E = hν = 2πħν,
where, 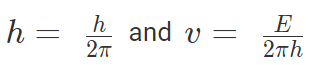
Smallest particles exhibit dual nature of particle and wave. De Broglie related the momentum of the particle and wavelength of the corresponding wave as follows-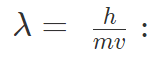
where, h is Planck’s constant, m is the mass and v is the velocity of the particle.
De Broglie relation can be written as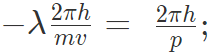
where, p is the momentum.
Electron as a particle-wave, moving in one single plane with total energy E, has an
Amplitude = Wave function = Ψ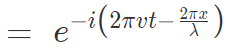
Substituting for wavelength and energy in this equation,
Amplitude = Wave function = Ψ
Now partial differentiating with respect to x,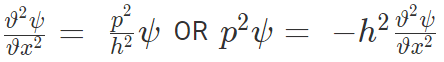
Also partial differentiating with respect to t,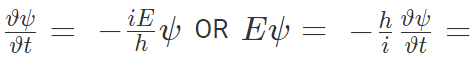
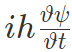
Conservation of Energy
Total energy is the sum of the kinetic and potential energy of the particle.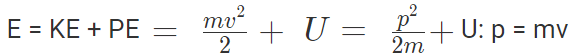
Substituting in the wave function equation,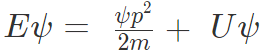
Substituting for EΨ and p2Ψ, we get the wave function for one-dimensional wave called “Time-dependent Schrodinger wave equation”.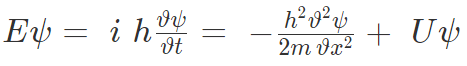
Time dependent Schrodinger equation for three-dimensional progressive wave then is,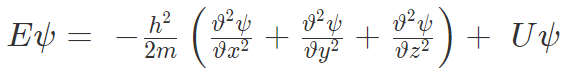
On rearranging,
The equation is also written as-

Schrödinger equation is written as HΨ = EΨ, where h is said to be a Hamiltonian operator.
Hydrogen Atom and the Schrödinger Equation
When scientists use the Schrödinger equation to understand the hydrogen atom, it provides information about the possible energy levels an electron can have and the corresponding wave functions (ψ) associated with each energy level. Here's a simpler breakdown:
The solution reveals quantized energy states and their respective wave functions. These states are described by three quantum numbers:
- Principal Quantum Number (n): Describes the main energy level an electron occupies.
- Azimuthal Quantum Number (l): Indicates the shape of the orbital within that energy level.
- Magnetic Quantum Number (ml): Specifies the orientation of the orbital in space.
When an electron is in a specific energy state, its wave function (ψ) holds all the information about that electron. However, this wave function is a mathematical concept and doesn't have a direct physical meaning. In the context of hydrogen or hydrogen-like species with just one electron, these wave functions are called atomic orbitals. They are considered one-electron systems.
The probability of finding an electron at a particular point within an atom is linked to the square of the wave function, denoted as |ψ|². These quantum mechanical results for the hydrogen atom accurately predict various aspects of its spectrum, even explaining phenomena that the earlier Bohr model couldn't account for.
Challenges in Using Schrödinger Equation for Multi-Electron Atoms:
- When dealing with atoms that have more than one electron, applying the Schrödinger equation becomes tricky. It's a challenge because the equation can't be solved exactly for these multi-electron atoms. To overcome this hurdle, scientists use approximate methods. Modern computers help perform these calculations, revealing that orbitals in atoms (other than hydrogen) don't drastically differ from hydrogen orbitals.
- The main distinction comes from an increased nuclear charge, causing all orbitals to be somewhat contracted. Additionally, unlike hydrogen or similar species, where orbital energies depend only on the quantum number n, in multi-electron atoms, orbital energies are influenced by both quantum numbers n and l.
Graphs for Various Wave Functions
Radial wave function (Ψ(r))
In all cases, R or Ψ approaches zero as r approaches infinity. One finds that there is a node in the 2s radial function. In general, it has been found that ns-orbitals have (n-1) nodes, np-orbitals have (n-2) nodes, etc.
The importance of these plots lies in the fact that they give information about how the radial wave function changes with distance r and about the presence of nodes where the change of sign of R occurs.
Variation of R with r.
Radial Probability density (Ψ2(r))
The square of the radial wave function Ψ2 or R2 for an orbital gives the radial density. The radial density gives the probability density of finding the electron at a point along a particular radius line. To get such a variation, the simplest procedure is to plot R2 against r. These plots give useful information about probability density or relative electron density at a point as a function of radius. It may be noted that while for s-orbitals the maximum electron density is at the nucleus. all other orbitals have zero electron density at the nucleus.
Plot of R2 with r.
Radial probability functions 4πr2Ψ2
The radial density Ψ2 R2 for an orbital, as discussed above, gives the probability density of finding the electron at a point at a distance r from the nucleus. Since the atoms have spherical symmetry, it is more useful to discuss the probability of finding the electron in a spherical shell between the spheres of radius (r dr) and r. The volume of the shell is equal to 4/3π(r dr)3-4/3πr3 = 4πr2dr.
This probability which is independent of direction is called radial probability and is equal to 4πr2drR2.
The radial probability function (4πr2drR2) gives the probability of finding the electron at a distance r from the nucleus regardless of direction.
The radial probability distribution curves obtained by plotting radial probability functions versus distance r from the nucleus for 1s, 2s, and 2p orbitals are shown in figures below:
Hydrogen 1s Radial Probability
Hydrogen 3s Radial Probability
Hydrogen 3p Radial Probability
Hydrogen 3d Radial Probability
Angular wave Function QF.
The angular wave function ' Q F ' depends only on the quantum number l and ml and is independent of the principal quantum number n for a given type of orbital. It therefore means that all s orbitals will have the same angular wave function.
(A) Angular Wave Function, ' Q F '
For an s-orbital, the angular part is independent or angle and is, therefore, of constant value. Hence this graph is circular or, more properly, in three dimensions i.e., spherical. For the pz orbital, we get two tangent spheres. The px and py orbitals are identical in shape but are oriented along the x and y axes respectively. The angular, wave function plots for d and f-orbitals are four lobed and six-lobed respectively.
It is necessary to keep in mind that in the angular wave function plots, the distance from the center is proportional to the numerical values of ' Q F ' in that direction and is not the distance from the center of the nucleus.
(B) Angular Probability Density, | Q F |2
The angular probability density plots can be obtained by squaring the angular function plots shown in fig. On squaring, different orbitals change in different ways. For an s orbital, the squaring causes no change in shape since the function everywhere is the same: thus another sphere is obtained.
Fig: Angular wave function.
Important Questions For Schrödinger Equation
1. What is a wave function?
Answer: Wave function is used to describe ‘matter waves’. Matter waves are very small particles in motion having a wave nature – dual nature of particle and wave. Any variable property that makes up the matter waves is a wave function of the matter wave. Wave function is denoted by a symbol ‘Ψ’. Amplitude, a property of a wave, is measured by following the movement of the particle with its Cartesian coordinates with respect of time. The amplitude of a wave is a wave function. The wave nature and the amplitudes are a function of coordinates and time, such that, Wave function Amplitude = Ψ = Ψ(r, t); where, ‘r’ is the position of the particle in terms of x, y, z directions.
2. What is meant by stationary state and what is its relevance to atom?
Answer: Stationary state is a state of a system, whose probability density given by | Ψ2 | is invariant with time. In an atom, the electron is a matter wave, with quantized angular momentum, energy, etc. Movement of the electrons in their orbit is such that probability density varies only with respect to the radius and angles. The movement is akin to a stationary wave between two fixed ends and independent of time. Wave function concept of matter waves are applied to the electrons of an atom to determine its variable properties.
3. What is the physical significance of the Schrödinger wave function?
Answer: Bohr's concept of an atom is simple. However, it cannot explain the presence of multiple orbitals and the fine spectrum arising out of them. It is applicable only to the one-electron system. Schrodinger wave function has multiple unique solutions representing characteristic radius, energy, and amplitude. The probability density of the electron calculated from the wave function shows multiple orbitals with unique energy and distribution in space. Schrodinger equation could explain the presence of multiple orbitals and the fine spectrum arising out of all atoms, not necessarily hydrogen-like atoms.
4. What is the Hamilton operator used in the Schrödinger equation?
Answer: In mathematics, the operator is a rule, that converts observed properties into another property. For example, ‘A’ will be an operator if it can change a property f(x) into another f(y). f(x)= f(y) Hamiltonian operator is the sum of potential and kinetic energies of particles calculated over three coordinates and time.
Hamiltonian operator = Ȟ = T + V = Kinetic energy + Potential energy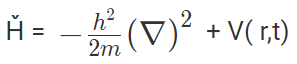
5. The electrons are more likely to be found: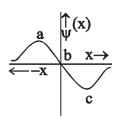 (1) in the region a and b
(1) in the region a and b
(2) in the region a and c
(3) only in the region c
(4) only in the region a
Region a and c has the maximum amplitude (Ψ) and hence the maximum probability density of Electrons | Ψ2|
Answer: (2)
|
114 videos|263 docs|74 tests
|
FAQs on Quantum Mechanical Model of Atom - Chemistry Class 11 - NEET
| 1. What is the need for Quantum Mechanics? |  |
| 2. What are the features of the Quantum Mechanical Model of an atom? |  |
| 3. How is the Schrödinger Wave Equation derived? |  |
| 4. How does the Schrödinger Equation describe the hydrogen atom? |  |
| 5. Can you provide examples of graphs for various wave functions in Quantum Mechanics? |  |





















