Second Law of Motion | Physics for JAMB PDF Download
| Table of contents |

|
| What is Newton’s Second Law of Motion? |

|
| What is a Net Force? |

|
| Application of Second Law |

|
| Impulse |

|
| Newton’s Second Law Solved Examples |

|
What is Newton’s Second Law of Motion?
Force is equal to the rate of change of momentum. For a constant mass, force equals mass times acceleration.
Newton’s second law of motion, unlike the first law of motion pertains to the behavior of objects for which all existing forces are unbalanced. The second law of motion is more quantitative and is used extensively to calculate what happens in situations involving a force.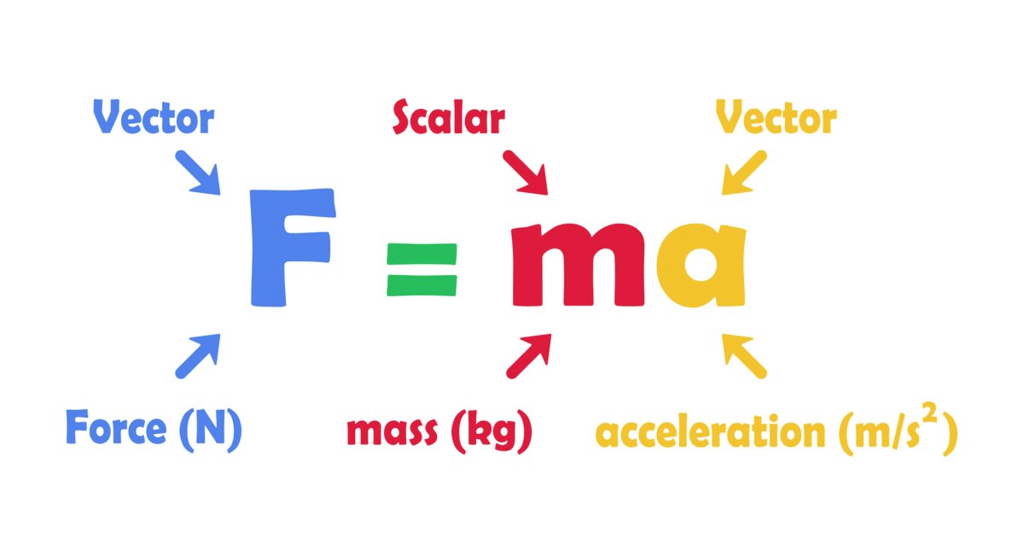 Representation of Second Law of Motion
Representation of Second Law of Motion
Defining Newton’s Second Law of Motion
- Newton’s second law states that the acceleration of an object depends upon two variables – the net force acting on the object and the mass of the object.
- The acceleration of the body is directly proportional to the net force acting on the body and inversely proportional to the mass of the body.
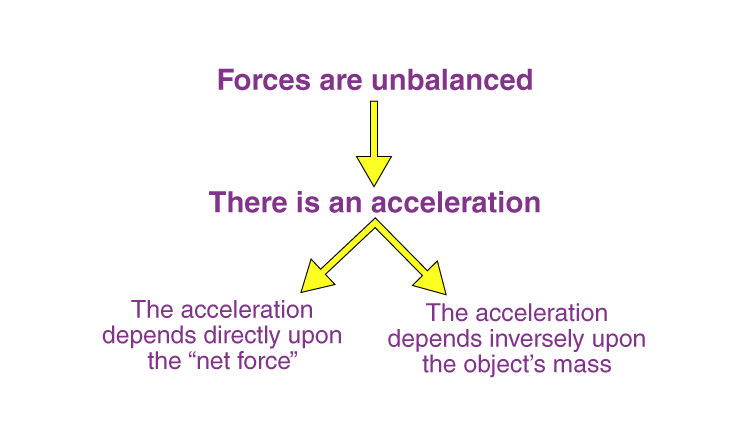
- This means that as the force acting upon an object is increased, the acceleration of the object is increased. Likewise, as the mass of an object is increased, the acceleration of the object is decreased.
Newton’s second law can be formally stated as:
The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.
This statement is expressed in equation form as:
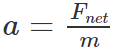
The above equation can be rearranged to a familiar form as:
F = ma
Since force is a vector, Newton’s second law can be written as: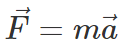
The equation shows that the direction of the total acceleration vector points in the same direction as the net force vector.
Deriving Newton’s Second Law
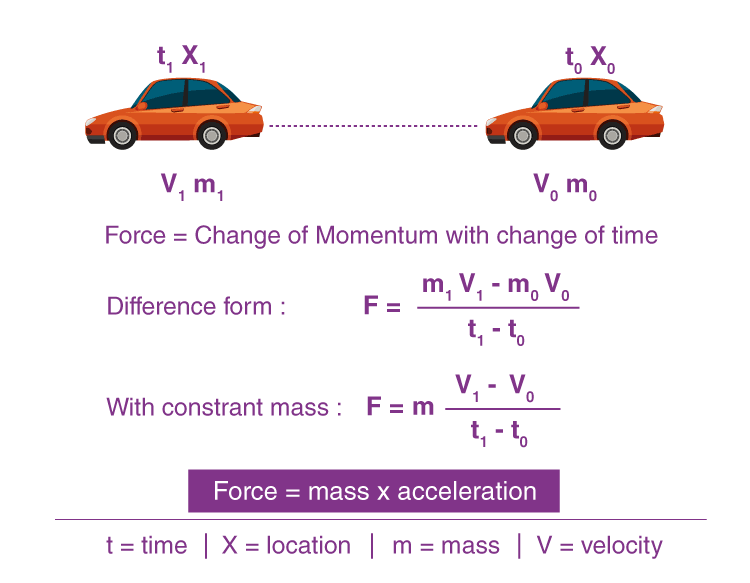
- Let us assume that we have a car at a point (0) defined by location X0 and time t0. The car has a mass m0 and travels with a velocity v0.
- After being subjected to a force F, the car moves to point 1 which is defined by location X1 and time t1. The mass and velocity of the car change during the travel to values m1 and v1.
- Newton’s second law helps us determine the new values of m1 and v1 if we know the value of the acting force.
- Taking the difference between point 1 and point 0, we get an equation for the force acting on the car as follows:
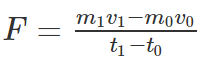
Let us assume the mass to be constant. This assumption is good for a car because the only change in mass would be the fuel burned between point “1” and point “0”. The weight of the fuel is probably small relative to the weight of the rest of the car, especially if we only look at small changes in time. Meanwhile, if we were discussing the flight of a bottle rocket, then the mass does not remain constant and we can only look at changes in momentum.
2. For Constant Mass
- For a constant mass, Newton’s second law can be equated as follows:
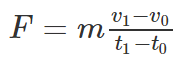
- We know that acceleration is defined as the change in velocity divided by the change in time. The second law then reduces to a more familiar form as follows: F = ma
- The above equation tells us that an object will accelerate if it is subjected to an external force and the amount of force is directly proportional to the acceleration and inversely proportional to the mass of the object.
What is a Net Force?
- A net force ΣF is the sum of all forces acting on a body. More precisely, it is the vector sum of all forces acting on a body.
 Force on a Body
Force on a Body - Consider two forces of magnitude 30 N and 20 N that are exerted to the right and left respectively on the horse shown in the picture.
- If we assume the rightward direction as positive, then the net force on the horse can be calculated as follows:
∑F = 30N − 20N = 10N
∑F = 10 N to the right
Application of Second Law
The application of the second law of motion can be seen in identifying the amount of force needed to make an object move or to make it stop.
Following are a few examples that we have listed to help you understand this point:
- Kicking a ball
When we kick a ball we exert force in a specific direction, which is the direction in which it will travel. In addition, the stronger the ball is kicked, the stronger the force we put on it and the further away it will travel. - Pushing a cart
It is easier to push an empty cart in a supermarket than it is to push a loaded one. More mass requires more force to accelerate. - Two people walking
Among the two people walking, if one is heavier than the other then the one weighing heavier will walk slower because the acceleration of the person weighing lighter is greater.
Impulse
- Sometimes, we see situations where a really strong push happens quickly and changes an object's movement.
- For instance, when a ball hits a wall and bounces back, the force from the wall acts only for a short time, but it's powerful enough to make the ball go in the opposite direction.
- Figuring out the force and time separately can be tricky, but we can measure their combined effect, which is called impulse. Impulse is the product of force and time, and it represents the change in momentum of the object.
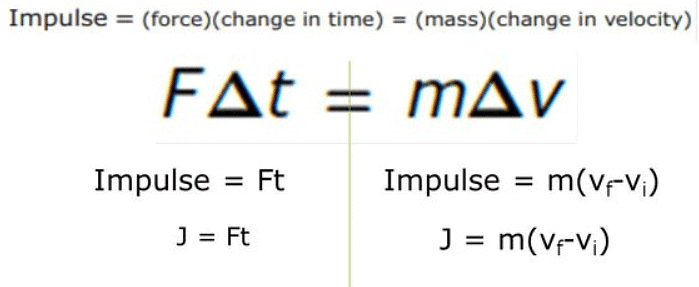 Impulse Equation
Impulse Equation
- When a strong force acts for a short time to create a noticeable change in momentum, it's called an impulsive force. In science, impulsive forces used to be considered different from regular forces, but Newtonian mechanics doesn't make that distinction. Impulsive force is essentially like any other force, just stronger and quicker.
Newton’s Second Law Solved Examples
Example 1: If there is a block of mass 2kg, and a force of 20 N is acting on it in the positive x-direction, and a force of 30 N in the negative x-direction, then what would be its acceleration?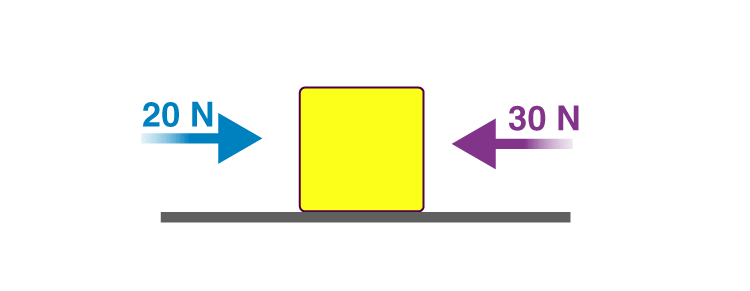 Solution: To calculate its acceleration, we first have to calculate the net force acting on it.
Solution: To calculate its acceleration, we first have to calculate the net force acting on it.
Fnet = 20 N – 30 N = -10 N
Mass = 2kg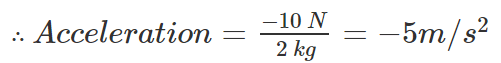
The negative acceleration indicates that the block is slowing and its acceleration vector is moving in an opposite direction directed opposite to the direction of motion.
Example 2: How much horizontal net force is required to accelerate a 1000 kg car at 4 m/s2?
Solution: Newton’s 2nd Law relates an object’s mass, the net force on it, and its acceleration. Therefore, we can find the force as follows:
Fnet = ma
Substituting the values, we get
1000 kg × 4 m/s2 = 4000 N
Therefore, the horizontal net force is required to accelerate a 1000 kg car at 4 m/s2 is 4000 N.
Newton’s second law is applied in daily life to a great extent. For instance, in Formula One racing, the engineers try to keep the mass of cars as low as possible. Low mass will imply more acceleration, and the more the acceleration, the chances to win the race are higher.
|
260 videos|253 docs|230 tests
|
FAQs on Second Law of Motion - Physics for JAMB
| 1. What is Newton's Second Law of Motion? |  |
| 2. What is a Net Force? |  |
| 3. What are some applications of Newton's Second Law? |  |
| 4. Can you provide some solved examples of Newton's Second Law? |  |
| 5. What are some frequently asked questions about Newton's Second Law? |  |