Bayes’s Theorem for Conditional Probability | Engineering Mathematics - Engineering Mathematics PDF Download
| Table of contents |

|
| Bayes’s formula |

|
| Product Rule |

|
| Chain rule |

|
| Bayes’ Theorem |

|
Bayes’s formula
Below is Bayes’s formula.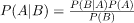
The formula provides the relationship between P(A|B) and P(B|A). It is mainly derived from conditional probability formula
Consider the below formulas for conditional probabilities P(A | B) and P(B | A)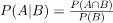 —(1)
—(1)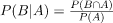 —(2)
—(2)
Since P(B ∩ A) = P(A ∩ B), we can replace P(A ∩ B) in the first formula with P(B | A)P(A)
After replacing, we get the given formula.
Product Rule
Product rule states that
P(X ∩ Y) = P(X | Y) * P(Y)
So the joint probability that both X and Y will occur is equal to the product of two terms:
From the product rule: implies P(X | Y) = P(X) / P(Y)
implies P(X | Y) = P(X) / P(Y) implies P(X | Y) = 1
implies P(X | Y) = 1
Chain rule
When the above product rule is generalized we lead to chain rule. Let there are E1, E2, E3, .....En n events . Then, the joint probability is given by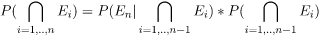 ..........(2)
..........(2)
Bayes’ Theorem
From the product rule, P(X ∩ Y) = P(X | Y)P(Y) and P(Y ∩ X) = P(X | Y)P(X). As P(X ∩ Y) and P(Y ∩ X) are same .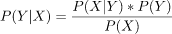 .............(3)
.............(3)
where P(X) = P(X ∩ Y) + P(X ∩ Yc)
Example: Box P has 2 red balls and 3 blue balls and box Q has 3 red balls and 1 blue ball. A ball is selected as follows:
(i) Select a box
(ii) Choose a ball from the selected box such that each ball in the box is equally likely to be chosen. The probabilities of selecting boxes P and Q are (1/3) and (2/3), respectively.
Given that a ball selected in the above process is a red ball, the probability that it came from the box P is (GATE CS 2005)
(a) 4 / 19
(b) 5 / 19
(c) 2 / 9
(d) 19/30
Solution:
R → Event that red ball is selected
B → Event that blue ball is selected
P → Event that box P is selected
Q → Event that box Q is selected
We need to calculate P(P | R)?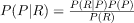
P(R | P) = A red ball selected from box P
= 2 / 5
P(P) = 1 / 3
P(R) = P(P) * P(R | P) + P(Q) * P(R|Q)
= (1 / 3) * (2 / 5) + (2 / 3) * (3 / 4)
= 2 / 15 + 1 / 2
= 19 / 30
Putting above values in the Bayes's Formula
P(P | R) = (2 / 5) * (1 / 3) / (19 / 30)
= 4 / 19.
|
65 videos|129 docs|94 tests
|
FAQs on Bayes’s Theorem for Conditional Probability - Engineering Mathematics - Engineering Mathematics
| 1. What is Bayes's formula? |  |
| 2. What is the Product Rule in probability theory? |  |
| 3. What is the Chain Rule in probability theory? |  |
| 4. What is Bayes' Theorem used for in conditional probability? |  |
| 5. How can Bayes' Theorem be applied in real-world scenarios? |  |















