Topological Sorting | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge u v, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.
For example, a topological sorting of the following graph is “5 4 2 3 1 0”. There can be more than one topological sorting for a graph. For example, another topological sorting of the following graph is “4 5 2 3 1 0”. The first vertex in topological sorting is always a vertex with in-degree as 0 (a vertex with no incoming edges).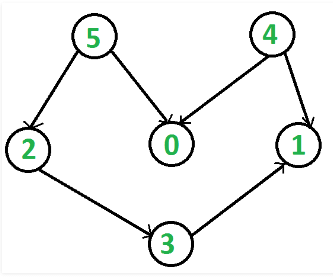 Topological Sorting vs Depth First Traversal (DFS):
Topological Sorting vs Depth First Traversal (DFS):
In DFS, we print a vertex and then recursively call DFS for its adjacent vertices. In topological sorting, we need to print a vertex before its adjacent vertices. For example, in the given graph, the vertex ‘5’ should be printed before vertex ‘0’, but unlike DFS, the vertex ‘4’ should also be printed before vertex ‘0’. So Topological sorting is different from DFS. For example, a DFS of the shown graph is “5 2 3 1 0 4”, but it is not a topological sorting.
Algorithm to find Topological Sorting:
We recommend to first see the implementation of DFS. We can modify DFS to find Topological Sorting of a graph. In DFS, we start from a vertex, we first print it and then recursively call DFS for its adjacent vertices. In topological sorting, we use a temporary stack. We don’t print the vertex immediately, we first recursively call topological sorting for all its adjacent vertices, then push it to a stack. Finally, print contents of the stack. Note that a vertex is pushed to stack only when all of its adjacent vertices (and their adjacent vertices and so on) are already in the stack.
Below image is an illustration of the above approach:
Following are the implementations of topological sorting. Please see the code for Depth First Traversal for a disconnected Graph and note the differences between the second code given there and the below code.
C++
// A C++ program to print topological
// sorting of a DAG
#include <iostream>
#include <list>
#include <stack>
using namespace std;
// Class to represent a graph
class Graph {
// No. of vertices'
int V;
// Pointer to an array containing adjacency listsList
list<int>* adj;
// A function used by topologicalSort
void topologicalSortUtil(int v, bool visited[],
stack<int>& Stack);
public:
// Constructor
Graph(int V);
// function to add an edge to graph
void addEdge(int v, int w);
// prints a Topological Sort of
// the complete graph
void topologicalSort();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
// Add w to v’s list.
adj[v].push_back(w);
}
// A recursive function used by topologicalSort
void Graph::topologicalSortUtil(int v, bool visited[],
stack<int>& Stack)
{
// Mark the current node as visited.
visited[v] = true;
// Recur for all the vertices
// adjacent to this vertex
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
topologicalSortUtil(*i, visited, Stack);
// Push current vertex to stack
// which stores result
Stack.push(v);
}
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
void Graph::topologicalSort()
{
stack<int> Stack;
// Mark all the vertices as not visited
bool* visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// Call the recursive helper function
// to store Topological
// Sort starting from all
// vertices one by one
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortUtil(i, visited, Stack);
// Print contents of stack
while (Stack.empty() == false) {
cout << Stack.top() << " ";
Stack.pop();
}
}
// Driver Code
int main()
{
// Create a graph given in the above diagram
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
cout << "Following is a Topological Sort of the given "
"graph \n";
// Function Call
g.topologicalSort();
return 0;
}
Java
// A Java program to print topological
// sorting of a DAG
import java.io.*;
import java.util.*;
// This class represents a directed graph
// using adjacency list representation
class Graph {
// No. of vertices
private int V;
// Adjacency List as ArrayList of ArrayList's
private ArrayList<ArrayList<Integer> > adj;
// Constructor
Graph(int v)
{
V = v;
adj = new ArrayList<ArrayList<Integer> >(v);
for (int i = 0; i < v; ++i)
adj.add(new ArrayList<Integer>());
}
// Function to add an edge into the graph
void addEdge(int v, int w) { adj.get(v).add(w); }
// A recursive function used by topologicalSort
void topologicalSortUtil(int v, boolean visited[],
Stack<Integer> stack)
{
// Mark the current node as visited.
visited[v] = true;
Integer i;
// Recur for all the vertices adjacent
// to thisvertex
Iterator<Integer> it = adj.get(v).iterator();
while (it.hasNext()) {
i = it.next();
if (!visited[i])
topologicalSortUtil(i, visited, stack);
}
// Push current vertex to stack
// which stores result
stack.push(new Integer(v));
}
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
void topologicalSort()
{
Stack<Integer> stack = new Stack<Integer>();
// Mark all the vertices as not visited
boolean visited[] = new boolean[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// Call the recursive helper
// function to store
// Topological Sort starting
// from all vertices one by one
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortUtil(i, visited, stack);
// Print contents of stack
while (stack.empty() == false)
System.out.print(stack.pop() + " ");
}
// Driver code
public static void main(String args[])
{
// Create a graph given in the above diagram
Graph g = new Graph(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
System.out.println("Following is a Topological "
+ "sort of the given graph");
// Function Call
g.topologicalSort();
}
}
// This code is contributed by Aakash Hasija
Python
# Python program to print topological sorting of a DAG
from collections import defaultdict
# Class to represent a graph
class Graph:
def __init__(self, vertices):
self.graph = defaultdict(list) # dictionary containing adjacency List
self.V = vertices # No. of vertices
# function to add an edge to graph
def addEdge(self, u, v):
self.graph[u].append(v)
# A recursive function used by topologicalSort
def topologicalSortUtil(self, v, visited, stack):
# Mark the current node as visited.
visited[v] = True
# Recur for all the vertices adjacent to this vertex
for i in self.graph[v]:
if visited[i] == False:
self.topologicalSortUtil(i, visited, stack)
# Push current vertex to stack which stores result
stack.append(v)
# The function to do Topological Sort. It uses recursive
# topologicalSortUtil()
def topologicalSort(self):
# Mark all the vertices as not visited
visited = [False]*self.V
stack = []
# Call the recursive helper function to store Topological
# Sort starting from all vertices one by one
for i in range(self.V):
if visited[i] == False:
self.topologicalSortUtil(i, visited, stack)
# Print contents of the stack
print(stack[::-1]) # return list in reverse order
# Driver Code
g = Graph(6)
g.addEdge(5, 2)
g.addEdge(5, 0)
g.addEdge(4, 0)
g.addEdge(4, 1)
g.addEdge(2, 3)
g.addEdge(3, 1)
print ("Following is a Topological Sort of the given graph")
# Function Call
g.topologicalSort()
# This code is contributed by Neelam Yadav
C#
// A C# program to print topological
// sorting of a DAG
using System;
using System.Collections.Generic;
// This class represents a directed graph
// using adjacency list representation
class Graph {
// No. of vertices
private int V;
// Adjacency List as ArrayList
// of ArrayList's
private List<List<int> > adj;
// Constructor
Graph(int v)
{
V = v;
adj = new List<List<int> >(v);
for (int i = 0; i < v; i++)
adj.Add(new List<int>());
}
// Function to add an edge into the graph
public void AddEdge(int v, int w) { adj[v].Add(w); }
// A recursive function used by topologicalSort
void TopologicalSortUtil(int v, bool[] visited,
Stack<int> stack)
{
// Mark the current node as visited.
visited[v] = true;
// Recur for all the vertices
// adjacent to this vertex
foreach(var vertex in adj[v])
{
if (!visited[vertex])
TopologicalSortUtil(vertex, visited, stack);
}
// Push current vertex to
// stack which stores result
stack.Push(v);
}
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
void TopologicalSort()
{
Stack<int> stack = new Stack<int>();
// Mark all the vertices as not visited
var visited = new bool[V];
// Call the recursive helper function
// to store Topological Sort starting
// from all vertices one by one
for (int i = 0; i < V; i++) {
if (visited[i] == false)
TopologicalSortUtil(i, visited, stack);
}
// Print contents of stack
foreach(var vertex in stack)
{
Console.Write(vertex + " ");
}
}
// Driver code
public static void Main(string[] args)
{
// Create a graph given
// in the above diagram
Graph g = new Graph(6);
g.AddEdge(5, 2);
g.AddEdge(5, 0);
g.AddEdge(4, 0);
g.AddEdge(4, 1);
g.AddEdge(2, 3);
g.AddEdge(3, 1);
Console.WriteLine("Following is a Topological "
+ "sort of the given graph");
// Function Call
g.TopologicalSort();
}
}
// This code is contributed by Abhinav Galodha
Output
Following is a Topological Sort of the given graph
5 4 2 3 1 0
Complexity Analysis:
- Time Complexity: O(V+E).
The above algorithm is simply DFS with an extra stack. So time complexity is the same as DFS which is. - Auxiliary space: O(V).
The extra space is needed for the stack.
Note: Here, we can also use vector instead of the stack. If the vector is used then print the elements in reverse order to get the topological sorting.
Applications:
Topological Sorting is mainly used for scheduling jobs from the given dependencies among jobs. In computer science, applications of this type arise in instruction scheduling, ordering of formula cell evaluation when recomputing formula values in spreadsheets, logic synthesis, determining the order of compilation tasks to perform in make files, data serialization, and resolving symbol dependencies in linkers .
|
159 docs|30 tests
|
FAQs on Topological Sorting - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is topological sorting in computer science engineering? |  |
| 2. How is topological sorting performed in computer science engineering? |  |
| 3. What is the time complexity of topological sorting in computer science engineering? |  |
| 4. Can topological sorting be applied to graphs with cycles in computer science engineering? |  |
| 5. What are some practical applications of topological sorting in computer science engineering? |  |





















