Mechanical Engineering Exam > Mechanical Engineering Notes > Strength of Materials (SOM) > Shear Stresses in Beams
Shear Stresses in Beams | Strength of Materials (SOM) - Mechanical Engineering PDF Download
Shearing Stress
In the theory of bending, presence of shear and the distortion of plane sections was neglected because the effect of it is not on bending stress is not of practical importance.
- But, it is important to consider the shear stresses for their own importance.
- Here, only the shearing stresses in the transverse palnes parallel to the shearing force and the complimentary shear stresses in the longitudinal planes parallel to the axis of the beam.
Fig. shows the rectangular cross-section of the beam, over which we have to determine the distribution of shear stress. Consider a layer ab at any above the N.A.

Shearing stress on a layer JK of beam at distance y from neutral axis.
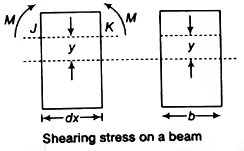
Where,
- V = Shearing force
 First moment of area
First moment of area
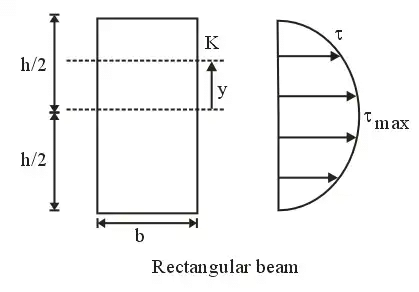
- Suppose, we have to determine the shear stress at the longitudinal layer having y distance from neutral axis.





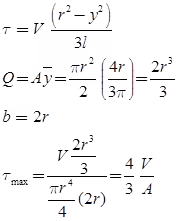
- Centre of gravity of semi-circle lies at distance from centre or base line. As it is symmetrical above neutral axis, hence at neutral axis shear stress will be maximum.

- For τmax substituting y = 0



Shears Stress in Hollow Circular Cross-Section
- In hollow circular cross-section, if we have to calculate τ at neutral axis by the formula

Shear Stress in Triangular Section
- In a triangular cross-section, if we have to calculate τ at neutral axis, then in formula


Shear Stress in I-section


Combined Stresses
Under combination of
- Direct Stress
σd = P/A
where P = axial thrust, A = area of cross-section
- Bending Stress
σb = My/l
where M = bending moment, y- distance of fibre from neutral axis, I = moment of inertia.
- Shear stresses
Τ = Tr/J
where T = torque, r = radius of shaft, J = polar moment of inertia.
Combined Stress is:
- Equivalent Torsional Moment:-
The equivalent torsional moment is defined as the torsional moment, which when acting alone, will produce the same torsional shear stress in the shaft as under the combined action of bending moment (Mb) and torsional moment (Mt)
- Equivalent Bending Moment:-
The equivalent Bending moment is defined as the bending moment, which when acting alone, will produce the same bending stresses (tensile and compressive) in the shaft as under the combined action of bending moment (Mb) and torsional moment (Mt)
Example:- A shaft of diameter 8 cm is subjected to a bending moment of 3000 Nm and a twisting moment of 4000 Nm. The maximum normal stress induced in the shaft is equal to
Solution:-
- Stress due to combined direct and bending load:
Suppose a beam under direct compressive and bending load as shown in the diagram. where A = Area,
y = distance of extreme fiber from Neutral axis and I = moment of Inertia Direct compressive stress σ = F/A
Direct compressive stress σ = F/A
Bending stress will vary linearly from center to extreme fiber
σb = My/I
so, total stress at upper fibre = Direct compressive stress+ tensile stress due to a bending load
= (-σ)+σb
Same for lower extreme fiber = Direct compressive stress+ Compressive stress due to bending load
=(-σ)+(-σb)
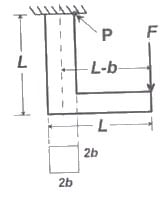
Example-
For the component loaded with a force F as shown in the figure, the axial stress at the corner point P is Solution:-
Solution:-
At point P two types of stress are acting, bending & axial tensile loadSo, bending stress =

Axial tensile stress =
Total axial stress at P = σb + σa
The document Shear Stresses in Beams | Strength of Materials (SOM) - Mechanical Engineering is a part of the Mechanical Engineering Course Strength of Materials (SOM).
All you need of Mechanical Engineering at this link: Mechanical Engineering
|
37 videos|41 docs|47 tests
|
FAQs on Shear Stresses in Beams - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is a shear stress in beams? |  |
Ans. Shear stress in beams refers to the internal force that acts parallel to the cross-sectional area of the beam. It is responsible for the deformation and failure of beams under certain loads.
| 2. How is shear stress calculated in beams? |  |
Ans. Shear stress in beams can be calculated using the formula: Shear Stress = (Shear Force * Distance from the neutral axis) / (Area Moment of Inertia * Beam Depth). This formula takes into account the applied shear force, the distance from the neutral axis, and the geometric properties of the beam.
| 3. What are the factors affecting shear stresses in beams? |  |
Ans. Several factors can affect shear stresses in beams, including the magnitude and distribution of the applied loads, the shape and size of the beam's cross-section, and the material properties of the beam. Additionally, the presence of any openings or cutouts in the beam can also influence the shear stress distribution.
| 4. How does shear stress impact the design of beams? |  |
Ans. Shear stress plays a crucial role in the design of beams as it determines the beam's ability to resist shear forces without failure. Engineers must ensure that the shear stress within the beam remains within safe limits to prevent shear failure. It influences the selection of appropriate beam materials, dimensions, and reinforcement techniques.
| 5. What are the common failure modes associated with shear stresses in beams? |  |
Ans. The two common failure modes associated with shear stresses in beams are shear failure and web buckling. Shear failure occurs when the shear stress exceeds the shear strength of the material, leading to a sudden and catastrophic failure. Web buckling, on the other hand, is a gradual failure caused by the buckling of the web of a beam due to excessive shear stress. Both failure modes can have severe consequences and should be considered during beam design.
Related Searches

 First moment of area
First moment of area
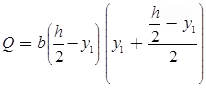

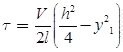








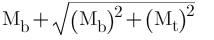

 Direct compressive stress σ = F/A
Direct compressive stress σ = F/A
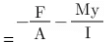
 Solution:-
Solution:-























