Probability Distributions (Uniform Distribution) | Engineering Mathematics - Engineering Mathematics PDF Download
Introduction
In probability theory and statistics, a probability distribution is a mathematical function that can be thought of as providing the probabilities of occurrence of different possible outcomes in an experiment. For instance, if the random variable X is used to denote the outcome of a coin toss (“the experiment”), then the probability distribution of X would take the value 0.5 for X = heads, and 0.5 for X = tails (assuming the coin is fair).
Probability distributions are divided into two classes
- Discrete Probability Distribution: If the probabilities are defined on a discrete random variable, one which can only take a discrete set of values, then the distribution is said to be a discrete probability distribution. For example, the event of rolling a die can be represented by a discrete random variable with the probability distribution being such that each event has a probability of 1/6.
- Continuous Probability Distribution: If the probabilities are defined on a continuous random variable, one which can take any value between two numbers, then the distribution is said to be a continuous probability distribution. For example, the temperature throughout a given day can be represented by a continuous random variable and the corresponding probability distribution is said to be continuous.
Cumulative Distribution Function
Similar to the probability density function, the cumulative distribution function F(x) of a real-valued random variable X, or just distribution function of X evaluated at x, is the probability that X will take a value less than or equal to x.
For a discrete Random Variable,
For a continuous Random Variable,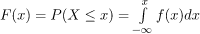
Uniform Probability Distribution
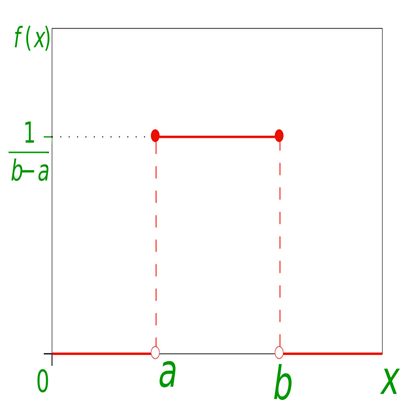
The Uniform Distribution, also known as the Rectangular Distribution, is a type of Continuous Probability Distribution.
It has a Continuous Random Variable X restricted to a finite interval [a,b] and it’s probability function f(x) has a constant density over this interval.
The Uniform probability distribution function is defined as:
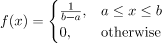
Expected or Mean Value: Using the basic definition of Expectation we get: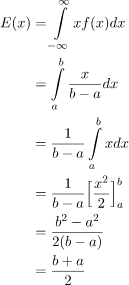
Variance: Using the formula for variance: V(X) = E(X2) - (E(X))2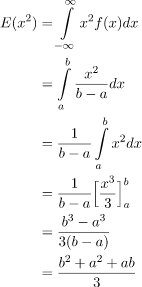
Using this result we get: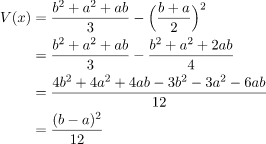
Standard Deviation: By the basic definition of standard deviation,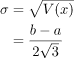
Example 1: The current (in mA) measured in a piece of copper wire is known to follow a uniform distribution over the interval [0, 25]. Find the formula for the probability density function f(x) of the random variable X representing the current. Calculate the mean, variance, and standard deviation of the distribution and find the cumulative distribution function F(x).
Solution: The first step is to find the probability density function. For a Uniform distribution, 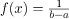 , where b, a are the upper and lower limit respectively.
, where b, a are the upper and lower limit respectively.
The expected value, variance, and standard deviation are-
The cumulative distribution function is given as-
There are three regions where the CDF can be defined, x < 0, 0 ≤ x ≤ 25, 25 < x
|
65 videos|129 docs|94 tests
|
FAQs on Probability Distributions (Uniform Distribution) - Engineering Mathematics - Engineering Mathematics
| 1. What is a uniform distribution? |  |
| 2. How is a uniform distribution different from other probability distributions? |  |
| 3. What is the probability density function of a uniform distribution? |  |
| 4. How can a uniform distribution be used in real-life applications? |  |
| 5. How can the mean and variance of a uniform distribution be calculated? |  |
















