EmSAT Achieve Exam > EmSAT Achieve Notes > Mathematics for EmSAT Achieve > Mean Value Theorem
Mean Value Theorem | Mathematics for EmSAT Achieve PDF Download
In mathematics, the mean value theorem states, roughly, that given a planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints.
The Mean Value Theorem states that if f(x) is continuous on [a, b] and differentiable on (a, b) then there exists a number c between a and b such that: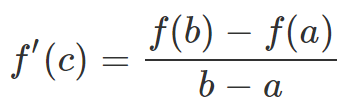
Solved Example
Question: Evaluate f(x) = x2 + 2 in the interval [1, 2] using mean value theorem.
Solution:
Given function is:
f(x) = x2 + 2
Interval is [1, 2].
i.e. a = 1, b = 2
Mean value theorem is given by,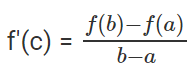
f(b) = f(2) = 22 + 2 = 6
f(a) = f(1) = 12 + 2 = 3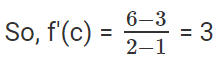 
The document Mean Value Theorem | Mathematics for EmSAT Achieve is a part of the EmSAT Achieve Course Mathematics for EmSAT Achieve.
All you need of EmSAT Achieve at this link: EmSAT Achieve
|
146 videos|222 docs|220 tests
|
About this Document
4.98/5
Rating
Sep 21, 2025
Last updated
Document Description: Mean Value Theorem for EmSAT Achieve 2025 is part of Mathematics for EmSAT Achieve preparation.
The notes and questions for Mean Value Theorem have been prepared according to the EmSAT Achieve exam syllabus. Information about Mean Value Theorem covers topics
like and Mean Value Theorem Example, for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mean Value Theorem.
Introduction of Mean Value Theorem in English is available as part of our Mathematics for EmSAT Achieve
for EmSAT Achieve & Mean Value Theorem in Hindi for Mathematics for EmSAT Achieve course.
Download more important topics related with notes, lectures and mock test series for EmSAT Achieve
Exam by signing up for free. EmSAT Achieve: Mean Value Theorem | Mathematics for EmSAT Achieve
Description
Full syllabus notes, lecture & questions for Mean Value Theorem | Mathematics for EmSAT Achieve - EmSAT Achieve | Plus excerises question with solution to help you revise complete syllabus for Mathematics for EmSAT Achieve | Best notes, free PDF download
Information about Mean Value Theorem
In this doc you can find the meaning of Mean Value Theorem defined & explained in the simplest way possible. Besides explaining types of
Mean Value Theorem theory, EduRev gives you an ample number of questions to practice Mean Value Theorem tests, examples and also practice EmSAT Achieve
tests
Related Searches
video lectures
,Extra Questions
,Exam
,Semester Notes
,past year papers
,Objective type Questions
,Mean Value Theorem | Mathematics for EmSAT Achieve
,MCQs
,Previous Year Questions with Solutions
,Summary
,shortcuts and tricks
,Free
,ppt
,mock tests for examination
,Viva Questions
,study material
,Important questions
,practice quizzes
,Mean Value Theorem | Mathematics for EmSAT Achieve
,Mean Value Theorem | Mathematics for EmSAT Achieve
,Sample Paper
;
Additional Information about Mean Value Theorem for EmSAT Achieve Preparation
Mean Value Theorem Free PDF Download
The Mean Value Theorem is an invaluable resource that delves deep into the core of the EmSAT Achieve exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Mean Value Theorem now and kickstart your journey towards success in the EmSAT Achieve exam.
Importance of Mean Value Theorem
The importance of Mean Value Theorem cannot be overstated, especially for EmSAT Achieve aspirants.
This document holds the key to success in the EmSAT Achieve exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Mean Value Theorem Notes
Mean Value Theorem Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Mean Value Theorem.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Mean Value Theorem Notes on EduRev are your ultimate resource for success.
Mean Value Theorem EmSAT Achieve Questions
The "Mean Value Theorem EmSAT Achieve Questions" guide is a valuable resource for all aspiring students preparing for the
EmSAT Achieve exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Mean Value Theorem on the App
Students of EmSAT Achieve can study Mean Value Theorem alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Mean Value Theorem,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Mean Value Theorem is prepared as per the latest EmSAT Achieve syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup