Probability Distributions (Binomial Distribution) | Engineering Mathematics - Engineering Mathematics PDF Download
Introduction
To understand the Binomial distribution, we must first understand what a Bernoulli Trial is. A Bernoulli trial is a random experiment with only two possible outcomes. These two outcomes are usually referred to as Success and Failure, but they may be given any label necessary. Each Bernoulli trial or a Random experiment is independent of the other.
For example, consider the scenario where we need to find the probability of the event of a even number showing up on die roll.
If E = Even number shows up, then
P(E) = 3 / 6 = 0.5 and,
P(E) = 1 - 3 / 6 = 0.5
Here P(E)(or simply ‘p’) may be referred to as the probability of Success and P(E)(or simply ‘q’) may be referred as the probability of Failure. Notice that, p + q = 1, since there are only two possible outcomes.
Now consider that the experiment is repeated and we try to find the probability of success. We get,
p = 0.5
This is the same probability as the first experiment. This is because the two experiments are independent i.e. the outcome of one experiment does not affect the other.
Now that we know what a Bernoulli trial is, we can move on to understand the Binomial Distribution.
A random experiment consists of n Bernoulli trials such that
- The trials are independent.
- Each trial results in only two possible outcomes, labeled as “success” and “failure.”
- The probability of a success in each trial, denoted as p, remains constant.
The random variable X that equals the number of trials that result in a success is a binomial random variable with parameters 0 < p < 1 and n = 1, 2, ….
The probability mass function is given by:
f(x) = (n / x) px(1 - p)n - x
Probability Mass Function
The above stated probability mass function is a legitimate probability function.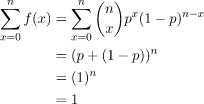
Notice that in the above formula, if we put n=1, we get the same result as a Bernoulli trial. Here x can take value 0 or 1(since number of successes can be 0 or 1 in one experiment).
P(Success) (1 / 1)p1 (1 - p)1 - 1 = p
P(Failure) = (1 / 0)p0(1 - p)1 - 0 = 1 - p = q
Here, p + q = 1
Expected Value
To find the Expected Value of the Binomial Distribution, let’s first find out the Expected value of a Bernoulli trial. Let p and q be the probabilities of Success(1) and Failure(0).
E[BT] = p * 1 + q * 0 = p
Since the Binomial Distribution has n Bernoulli trials, the expected Value is multiplied by n. This is due to the fact that each experiment is independent and the Expected value of the sum of Random variables is equal to the sum of their individual Expected Values. This property is also called the Linearity of Expectation.
E[X] = E[BT1] + E[BT2] + .... + E[BTn] = nE[BT] = np
Variance and Standard deviation
The variance of the Binomial distribution can be found in a similar way. For n independent Random Variables,
Var [X1 + X2 + ... + Xn] = Var[BT1] + Var[BT2] + ... + Var[BTn] = nVar[BT]
Here, Var[BT] is the Variance of 1 Bernoulli trial.
Var[BT] = E[X2] - E[X]2
= (p * (12) + q * (02)) - p2
= p - p2
= p(1 - p)
= Pq
Using this result to find out the variance of the Binomial Distribution.
Var[X] = nVar[BT] = npq
The Standard Deviation of the distribution: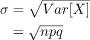
Example: An airline sells 65 tickets for a plane with capacity of 60 passengers. This is done because it is possible for some people to not show up. The probability of a person not showing up for the flight is 0.1. All passengers behave independently. Find the probability of the event that the airline does not have to arrange separate tickets for excess people.
Solution: If more than 60 people show up, then the airline has to reschedule tickets for the excess number of people. Let X be the random variable denoting the number of passengers that show up. We have to find the probability of the event where X <= 60.
Let p be the probability that a passenger shows up. p = 1 – 0.1 = 0.9.
q = 0.1
P(X ≤ 60) = 1 - P(X ≥ 61)
= 1 - (P(X = 61) + P(X = 62) + P(X = 63) + P(X = 64) + P(X = 65))
1 - ((65 / 61) p61q4 + (65 / 62)P62q3 + (65 / 63)p63q2 + (65 / 64)p64q1 + (65 / 65)p65q0)
= 1 - (0.1095 + 0.0636 + 0.0272 + 0.0077 + 0.0011)
= 1 - 0.2091
= 0.7909
|
65 videos|129 docs|94 tests
|
FAQs on Probability Distributions (Binomial Distribution) - Engineering Mathematics - Engineering Mathematics
| 1. What is a probability distribution? |  |
| 2. What is a binomial distribution? |  |
| 3. How is the probability calculated in a binomial distribution? |  |
| 4. What is the mean of a binomial distribution? |  |
| 5. How can the binomial distribution be used in real-life scenarios? |  |
















