Pressure Vessels (Thin Cylinder) | Strength of Materials (SOM) - Mechanical Engineering PDF Download
Introduction
Thin pressure vessel is defined as a closed cylindrical or spherical container designed to hold or store fluids at a pressure substantially different from ambient pressure. Pressure vessels can be classified as
(i) on the basis of ratio of diameter to its thickness
where, D is the inner diameter of the shell & t is the thickness of the shell.
(ii) On the basis of shape of the pressure vessel
However, Spherical pressure vessels are better, but due to fabrication difficulty, cylindrical pressure vessels are most commonly used.
Common examples of pressure vessels are steam boilers, reservoirs, tanks, working chambers of engines, gas cylinders etc.
Thin Cylindrical Shell Subject To Internal Pressure
Consider a thin cylinder of internal diameter d and wall thickness t, subject to internal gauge pressure P. The following stresses are induced in the cylinder-
(a) Circumferential tensile stress (or hoop stress) σH.
(b) Longitudinal (or axial) tensile stress σL.
(c) Radial compressive stress σR which varies from a value at the inner surface equal to the atmosphere pressure at the outside surface.
Assumptions followed in thin pressure vessels
- Stresses are assumed to be distributed uniformly
- Area is calculated considering the pressure vessel as thin
- Radial stresses are neglected
- Biaxial state of stress is assumed to be applicable
(a) Circumferential stress or Hoop stress, σH
There are normal stresses which act in the direction of circumference. Due to internal fluid pressure these are tensile in nature. In thin pressure vessels, hoop stresses are assumed to be uniform across thickness.
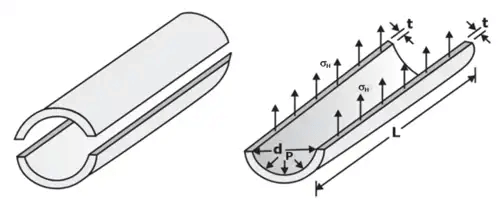
In the figure we have shown a one half of the cylinder. This cylinder is subjected to an internal pressure P.
Pressure force by fluid ≤ Resisting force owing to hoop stresses σH
P x Projected Area ≤ 2.σh.L.t
P.d.L ≤ 2.σh.L.t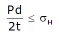
For equilibrium σH = pd/2t
In ηL is the efficiency of the Longitudinal riveted joint,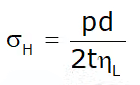
Similarly,
(b) Longitudinal stress (or axial stress) σL
Pressure force by fluid ≤ Resisting force owing to longitudinal stresses σL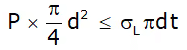
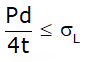
For equilibrium, σL = Pd/4t
In ηL is the efficiency of the circumferential riveted joint,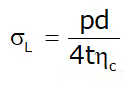
Thus, the magnitude of the longitudinal stress is one half of the circumferential stress, both the stresses being of tensile nature.
Hoop strain or Circumferential strain -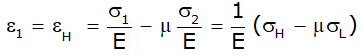
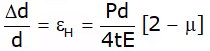
Longitudinal Strain or axial strain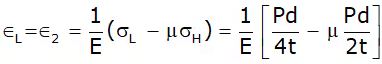
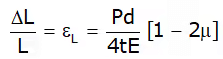
Ratio of Hoop Strain to Longitudinal Strain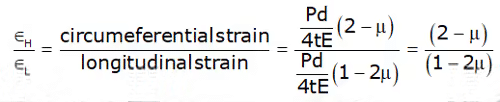
Volumetric Strain or Change in the Internal Volume
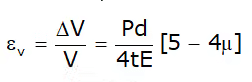
Thin Spherical Shells
Figure shows a thin spherical shell of internal diameter ‘d’ and thickness ‘t’ and subjected to an internal fluid pressure ‘P’.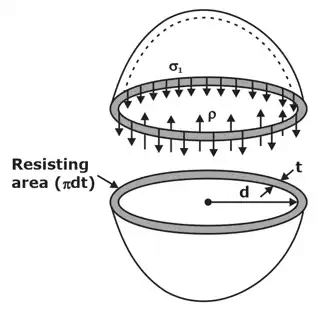
Hoop stress/longitudinal stress
Pressure force by fluid ≤ Resisting force owing to Hoop/Longitudinal stresses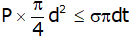
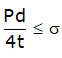
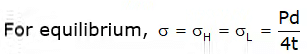
Hoop stress/longitudinal strain
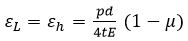
Volumetric strain of sphere
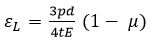
Thick Pressure Vessels
In thick vessels pressure vary from maximum at inner surface to minimum at outer surface.
(i) In thick cylinders hoop stress due to inside pressure is Maximum inside and Minimum outside
(ii) In thick cylinders longitudinal stress due to inside pressure is constant
(iii) Radial pressure is maximum inside, zero outside and compressive throughout.
Analysis of thick shells using lame’s theorem
In this theorem the material is assumed to be homogeneous and isotropic and the longitudinal stress are assumed to be constant throughout.
Hoop stress-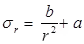
Radial pressure -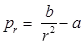
Where A & B are Lame’s constant and they and they are always positive.
By solving these two equations for different boundary conditions, we can find out value of A & B.
Subjected to only Internal Pressure (p), radial pressure at inside and outside radii is-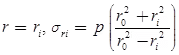
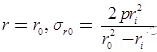
Subjected to External Pressure (p), radial pressure at inside and outside radii is-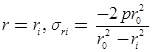
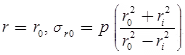
|
37 videos|39 docs|45 tests
|
FAQs on Pressure Vessels (Thin Cylinder) - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is a pressure vessel? |  |
| 2. What is a thin cylinder in the context of pressure vessels? |  |
| 3. What are the key design considerations for pressure vessels? |  |
| 4. How is the stress in a thin cylinder calculated? |  |
| 5. What are some common failure modes in pressure vessels? |  |






















