Inductance & Resistance of Transmission Lines | GATE Notes & Videos for Electrical Engineering - Electrical Engineering (EE) PDF Download
Inductance in Transmission Line
Reason of Transmission Line Inductance
Generally, electric power is transmitted through the transmission line with AC high voltage and current. High valued alternating current while flowing through the conductor sets up magnetic flux of high strength with alternating nature. This high valued alternating magnetic flux makes a linkage with other adjacent conductors parallel to the main conductor. Flux linkage in a conductor happens internally and externally. Internally flux linkage is due to self-current and externally flux linkage due to external flux. Now the term inductance is closely related to the flux linkage, denoted by λ. Suppose a coil with N number of turn is linked by flux Φ due to current I, then,
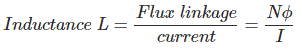
But for transmission line N = 1. We have to calculate only the value of flux Φ, and hence, we can get the transmission line inductance.
Calculation of Inductance of Single Conductor
Calculation of Internal Inductance due to Internal Magnetic Flux of a Conductor
Suppose a conductor is carrying current I through its length l, x is the internal variable radius of the conductor and r is the original radius of the conductor. Now the cross-sectional area with respect to radius x is πx2 square – unit and current Ix is flowing through this cross-sectional area. So the value of Ix can be expressed in term of original conductor current I and cross-sectional area πr2 square – unit

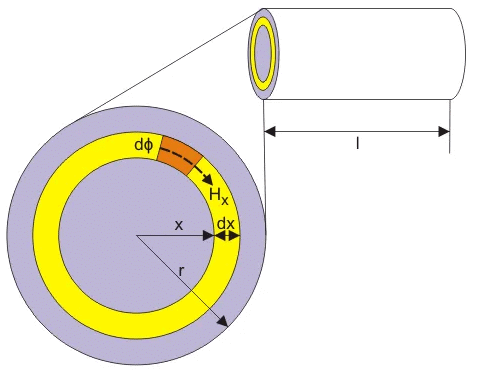
Now consider small thickness dx with the 1m length of the conductor, where Hx is the magnetizing force due to current Ix around the area πx2.
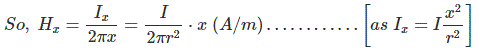
And magnetic flux density Bx = μHx, where μ is the permeability of this conductor. Again, µ = µ0µr. If it is considered that the relative permeability of this conductor µr = 1, then µ = µ0. Hence, here Bx = μ0 Hx.
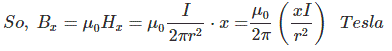
dφ for small strip dx is expressed by
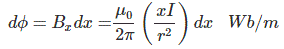
Here entire cross-sectional area of the conductor does not enclose the above expressed flux. The ratio of the cross sectional area inside the circle of radius x to the total cross section of the conductor can be thought about as fractional turn that links the flux. Therefore the flux linkage is
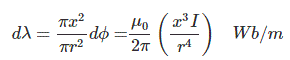
Now, the total flux linkage for the conductor of 1m length with radius r is given by
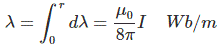
Hence, the internal inductance is
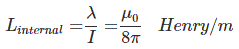
External Inductance due to External Magnetic Flux of a Conductor
Let us assume, due to skin effect conductor current I is concentrated near the surface of the conductor. Consider, the distance y is taken from the center of the conductor making the external radius of the conductor.
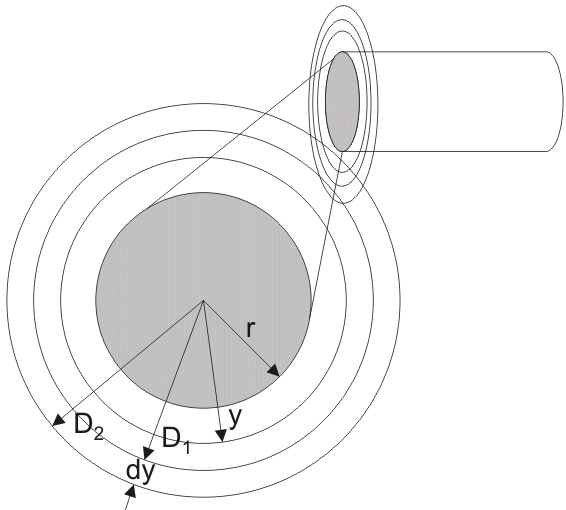
Hy is the magnetizing force and By is the magnetic field density at y distance per unit length of the conductor.
Now,
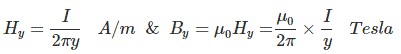
Let us assume magnetic flux dφ is present within the thickness dy from D1 to D2 for 1 m length of the conductor as per the figure.
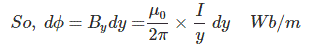
As the total current I is assumed to flow in the surface of the conductor, so the flux linkage dλ is equal to dφ.
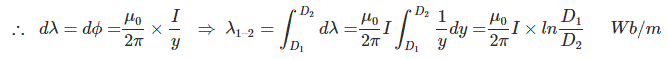
But we have to consider the flux linkage from conductor surface to any external distance, i.e. r to D
So,
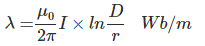
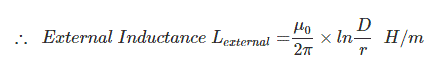

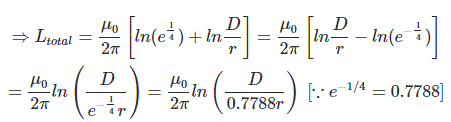

Inductance of Two Wire Single Phase Transmission Line
Suppose conductor A of radius rA carries a current of IA in opposite direction of current IB through the conductor B of radius rB. Conductor A is at a distance D from conductor B and both are of length l. They are in close vicinity with each other so that flux linkage takes place in both of the conductors due to their electromagnetic effects.
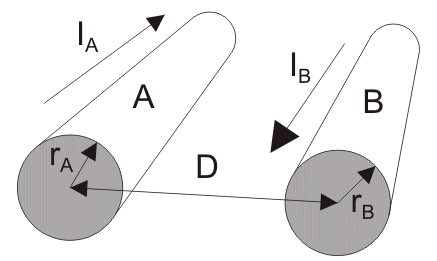
Let us consider the magnitude of current in both conductors are same and hence IA = – IB,
Now, total flux linkage in conductor A = flux linkage by self-current of conductor A + flux linkage on conductor A due to current in the conductor B.
Similarly, flux linkage in conductor B = flux linkage by self-current of conductor B + flux linkage on conductor B due to current through conductor A.
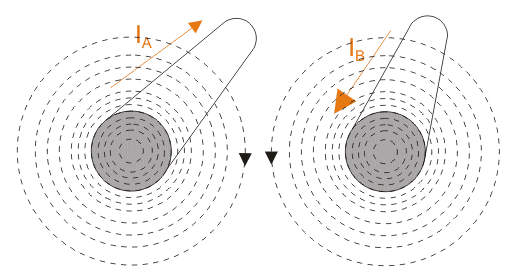
Now if we consider a point P in close vicinity both conductor A and B, the flux linkage at point P would be, flux linkage at point P for current carrying conductor A + flux linkage at point P for current carrying conductor B i.e.
λp = λAP + λBP
Now,
λ= λAP + λBP (λAAP + λABP) +(λBAP + λBBP)
……… shown in the figure below in figure (a) and (b).
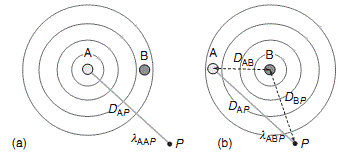
- λAAP is the flux linkage at point P for conductor A due to current through conductor A itself.
- λABP is the flux linkage at point P for conductor A due to current through conductor B.
- λBAP is the flux linkage at point P for conductor B due to current through conductor A.
- λBBP is the flux linkage at point P for conductor B due to current through conductor B itself.
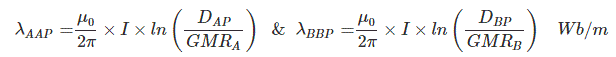
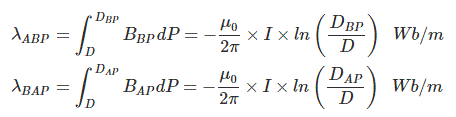
λABP and λBAP are negative in value because the directions current are opposite with respect to each other.
So,
λ= λAP + λBP = (λAAP + λABP) +(λBAP + λBBP)
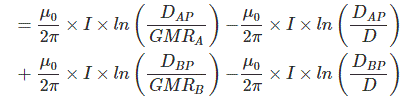
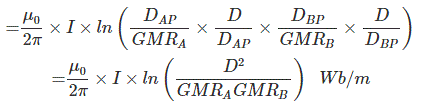
If we consider that both conductor are with same radius, i.e. rA = rB = r and point P is shifted to infinite distance then we can write that
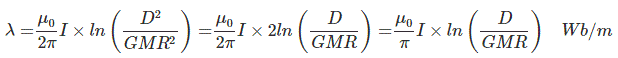
Therefore, inductance per phase
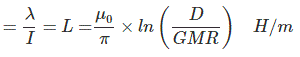
If conductor A becomes bundled conductor, then its geometrical mean radius (GMR) will be calculated for n number of conductors per bundle.

Where, d is the distance between the central axis of conductors within the bundle.
Inductance in Three Phase Transmission Line
In the three phase transmission line, three conductors are parallel to each other. The direction of the current is same through each of the conductors.
Let us consider conductor A produces magnetic flux φA,
Conductor B produces magnetic flux φB,
And conductor C produces magnetic flux φC.
When they carry the current of the same magnitude “I”, they are in flux linkage with each other.
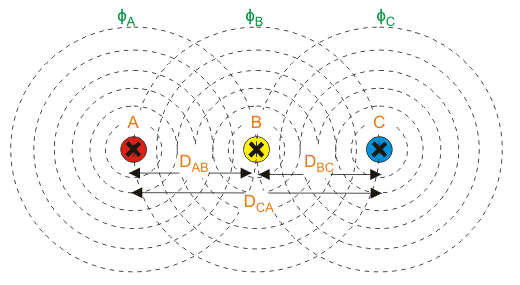
Now, let us consider a point P near three conductors. So, flux linkage at point P due to current through conductor A is,
λAP=λAAP + λABP + λACP
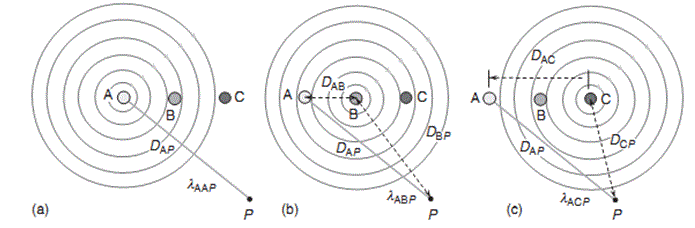
Flux linkage at point P for conductor A due to current through conductor A =
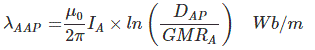
Flux linkage at point P for conductor A due to current through conductor B =
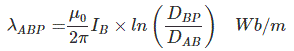
Flux linkage at point P for conductor A due to current through conductor C =

Therefore, flux linkage at point P for conductor A,
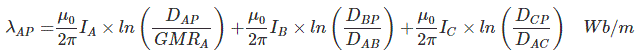

As,
DAP = DBP=DCP
and
IA+IB+IC= 0
in balanced system, then we can write that
IA= -IB - IC
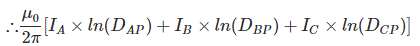
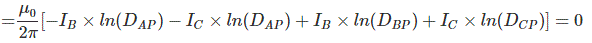
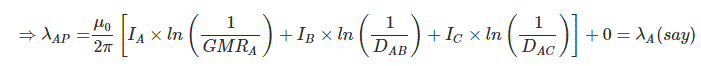
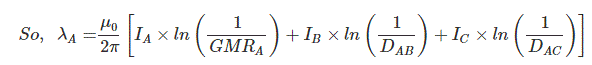
Similarly,
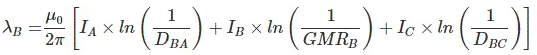
and
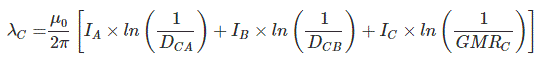
If we arrange them in matrix form, then we get
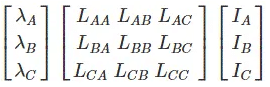
Where, λA, λB, λC are the total flux linkages of conductor A, B and C.
LAA, LBB and LCC are the self inductances of conductor A, B and C.
LAB, LAC, LBC, LBA, LCA, LCB are the mutual inductances of between conductors A, B and C.
Again balanced system
DAB =DBC = DCA =D
And
IA + IB + IC = 0
In balanced system, then we can write that
IA = - IB - IC
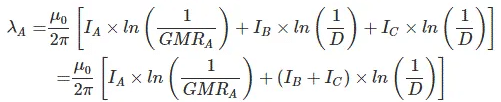
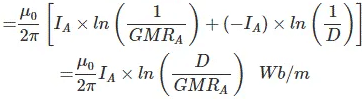
Similarly,
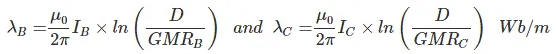
So, inductance per meter per phase,
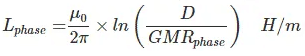
|
27 videos|328 docs
|
FAQs on Inductance & Resistance of Transmission Lines - GATE Notes & Videos for Electrical Engineering - Electrical Engineering (EE)
| 1. What is inductance in transmission lines? |  |
| 2. How does inductance affect transmission lines? |  |
| 3. How is inductance calculated in transmission lines? |  |
| 4. What is the significance of resistance in transmission lines? |  |
| 5. How does resistance affect the performance of transmission lines? |  |
|
27 videos|328 docs
|

|
Explore Courses for Electrical Engineering (EE) exam
|

|

















