Relationship between Zeroes & Coefficients of a Polynomial | The Complete SAT Course - Class 10 PDF Download
Any Algebraic expression with constants and variables is known as a Polynomial. Polynomial is a combination of two words, “Poly” and “nominal” where poly means “many” and nominal means “terms”, hence, a Polynomial can contain as many terms but never infinite. In a Polynomial, zeros and coefficients are present where the coefficients are already provided to us however, we need to obtain the value of zeros with the help of coefficients.
Relationship between Zeros and Coefficients
We know that zeros of any polynomial are the points where the graph of the polynomial cuts the x-axis. These zeros can also be found out using the coefficients of different terms in a polynomial. Let’s look at the relationship between the zeros and coefficients of the polynomials.
Linear Polynomial
A linear polynomial, in general, is defined by,
y = ax + b
We know, for zeros we need to find the points at which y = 0. Solving this general equation for y = 0.
y = ax + b
⇒ 0 = ax + b
⇒x = -b/a
This gives us the relationship between zero and the coefficient of a linear polynomial.
In general for a linear equation y = ax + b, a ≠ 0, the graph of ax + b is a straight line that cuts the x-axis at (-b/a, 0)
Question: Verify the zeros of the linear polynomial both using the formula mentioned above and the graphical method.
y = 4x + 2
Solution:
We are given with the equation y = 4x + 2,
Here a = 4 and b = 2
So, by the formula mentioned above the zero will occur at (-b/a, 0) that is (-2/4, 0) = (-1/2, 0)
Let’s verify this zero with graphical method. We need to plot the graph of this equation.
y = 4x + 2
Let’s bring it to the intercept form.
y/2 - 4x/2 = 1
Now we know the intercepts on the x and y-axis.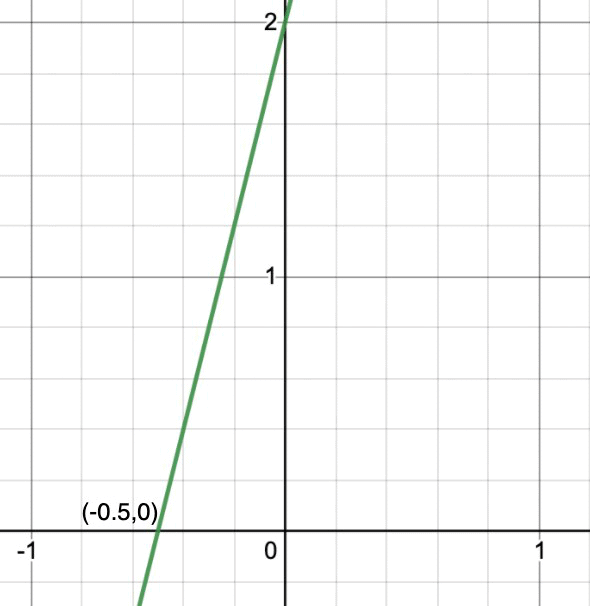
Quadratic Polynomial
Quadratic polynomials have the highest degree of 2 and along with factorization, there are other methods through which the zeros of the quadratic polynomial can be found such as Dharacharya method. As it has the highest degree 2, there exist 2 zeros in a quadratic polynomial.
Let’s derive the relationship between zeros and coefficients of a quadratic polynomial. Let’s assume a polynomial,
P(x) = 2x2 – 8x + 6
This polynomial can be factorized as follows,
P(x) = 2x2 -8x + 6
= 2x2 – 6x – 2x + 6
= 2x(x – 3) -2(x – 3)
= 2(x – 1)(x – 3)
So this equation has roots x = 1 and x = 3
Notice that,
Sum of zeros = 1 + 3 = 4 = 8/2 = -8/2 = - coefficient of x/coefficient of x2
Product of zeros = 1 × 3 = 3 = 6/2 = Constant Term/coefficient of x2
This is the relationship between zeros and coefficients for second-order coefficients.
So to put in a general form
For a polynomial, p(x) = ax2 + bx + c which has m and n as roots
m + n = -b/a
m × n = c/a
Question: Verify the property stated above for the equation, 6x2 – 10x + 4
Solution:
6x2 – 10x + 4
⇒ 6x2 – 6x -4x + 4
⇒ 6x(x – 1) – 4(x – 1)
⇒ (6x – 4) (x – 1)
Thus, the roots for this equation come out to be x = 4/6 = 2/3 and x = 1
Now we know according to above properties,
Sum of zeros = - coefficient of x/coefficient of x2
Product of zeros = Constant Term/coefficient of x2
Let’s verify it
Sun of zeros = 1 + 2/3 = 5/3
- coefficient of x/coefficient of x2 = -10/6 = 5/3
Both the values come to be equal. Hence, verified.
Let’s verify the product of roots property
Product of zeros = 2/3
- coefficient of x/coefficient of x2 = 2/3
In this case also, both values are equal. Hence, verified.
Cubic Polynomial
Similar relation can be derived for a cubic polynomial. A cubic polynomial is a polynomial of degree 3 and since it has its highest degree as 3, there exist three zeros of a cubic polynomial. Let’s suppose the roots/zeros of the polynomials obtained are p, q, r, the relationship between the zeros and polynomials will be given as,
For a cubic polynomial,
ax3 + bx2 + cx + d
Which has roots x = p, q and r
|
433 videos|220 docs|166 tests
|
FAQs on Relationship between Zeroes & Coefficients of a Polynomial - The Complete SAT Course - Class 10
| 1. What is the relationship between zeroes and coefficients of a polynomial? |  |
| 2. How can we find the sum of zeroes of a polynomial? |  |
| 3. How can we find the product of zeroes of a polynomial? |  |
| 4. Can a polynomial have more zeroes than its degree? |  |
| 5. Can the coefficients of a polynomial determine its zeroes? |  |
















