Derivatives of a Function | Mathematics (Maths) for JEE Main & Advanced PDF Download

What is a Derivative?

The derivative is a fundamental of Calculus. A derivative of functions follows the concept of limits. Within limits, we try to obtain the value of a function at different points. In a derivative, we look for the rate of change of a function. We also try to establish if the rate of change follows a definite pattern.
For example, while filling a bucket of water from the tp we need to know the rate of flow of water from the tap to determine in what time the bucket will be filled. Thus, in this case, the rate of flow of water is the derivative function we consider. Thus a derivative of functions is basically the rate of change of a value at a point.
A very common and easy to understand example of a derivative is the slope of a line. We know that the slope of a line can be calculated in many ways. It is also indicative of the tan of the angle of the line. The slope of a line is the rate of change of the value of points on the line.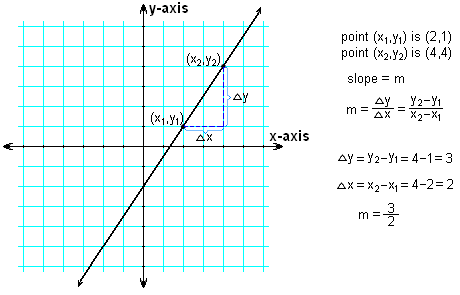

Definition of a Derivative of Functions

Let us assume a function f. Here, f is a real-valued function and ‘a’ is any point in the domain of the function. Then, the derivative of f is defined as
lim_h->0 (f (a+h) – f(a))/h
assuming that this limit exists. The derivative of f(x) at ‘a’  is denoted by f'(a) which signifies the change in f(x) at ‘a’ with respect to x.
For example: if  f(x) = 4x, find f ‘(x) at x = 4, then 
f'(4) = lim_h->0 ( f(4+h)-f(4))/h 
= (4(4+h)-4(4)) / h = lim_h->0 4h / h 
= 4 
Thus, derivative of 4x at x = 4 is 4. 
If the function lim_h->0 (f(a+h)-f(a))/ h  exists for a function ‘f’, it is called as the ‘first principle of derivative’. If y = f(x) then, the above function’s derivative can also be represented as dy/dx and at a point say ‘a’; f ‘(x) can be represented as (dy/dx)_x=a 

Derivatives of Some Basic Functions

• If y = ax , where a is a constant, dy/dx = a
• y = xⁿ , where n is an integer, dy/dx = nx^n-1 
• If y = sinx, dy/dx = cosx
• y = tanx, dy/dx = sec²x
• If y = a ,where ‘a’ is a constant, then dy/dx=0

Laws of Derivatives
Consider 2 funtions f(x) and g(x) whose derivatives are in the same domain, then

• Derivative of sum of 2 functions is same as the sum of derivatives of the functions
  d(f(x) +g(x))/dx = d(f(x))/dx + d(g(x))/dx
• Derivative of differnce of 2 functions is difference of derivatives of the 2 functions
  d(f(x)-g(x))=d(f(x))/dx – d(g(x))/dx

Leibnitz Rule

While we perform differentiation of 2 functions either in multiplication and /or divisiom we will use the rules mentioned below

• Derivative of product of 2 functions is given by the product rule. Let ‘u’ and ‘v’ be 2 functions then
  (uv)’ = u’v+ uv’
  d(f(x).g(x))= d(f(x))/dx.g(x) + f(x).d(g(x))/dx
• Derivative  of quotient of 2 functions is given by the quotient rule (if the denominator is non zero)
  (u/v)’ = ( u’v-uv’)/v² 
  d(f(x)/g(x))= (d(f(x))/dx .g(x) – d(g(x))/dx .f(x))/(g(x))² 

Solved Example for You
Question: Find f ‘(x) when f(x) = 1/x²
Solution: When f(x) = 1/x² = x^-2, using the above laws 
d(xⁿ)/dx = nx^n-1 
f ‘ (x) = -2x^-3 
f ‘ (x) = -2/x³