Rate of Change of Quantities | Mathematics (Maths) for JEE Main & Advanced PDF Download
Definition
If a quantity ‘y’ changes with a change in some other quantity ‘x’ given the fact that an equation of the form y = f(x) is always satisfied i.e. ‘y’ is a function of ‘x’; then the rate of change of ‘y’ with respect to ‘x’ is given by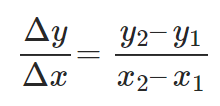
This is also sometimes simply known as the Average Rate of Change.
If the rate of change of a function is to be defined at a specific point i.e. a specific value of ‘x’, it is known as the Instantaneous Rate of Change of the function at that point. From the definition of the derivative of a function at a point, we have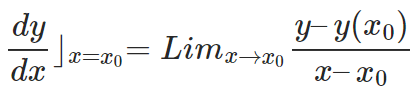
From this, one can conclude that the derivative of a function actually represents the Instantaneous Rate of Change of the function at that point. From the rate of change formula, it represents the case when Δx → 0. Thus, the rate of change of ‘y’ with respect to ‘x’ at x = x0 = 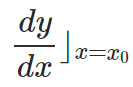
Note: If you plot a quantity ‘y’ as a function of the quantity ‘x’, then the derivative of ‘y’ with respect to ‘x’ represents the SLOPE of the tangent to the curve at that point. (We’ll discuss more tangents in a later section)
If the quantities ‘y’ and ‘x’ are themselves functions of another quantity, say ‘t’; then we can conveniently find the rate of change of y with respect to x from the formula: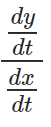
Solved Example
Question 1: A city’s population is modelled as P(t) = 2t2 + 10t + 200 persons(t is the number of years since 2000). What would be the average rate at which the population is changing in 2005?
Solution: For the average rate, we need the information at the beginning point and the endpoint of our domain. Clearly, the beginning point would be the year 2000 corresponding to which, we have t1 = 0 and P(t = 0) = 200. The endpoint: t2 = (2005-2000) = 5 corresponding to which, P(t = 5) = 300. The average rate of change of population in 2005: 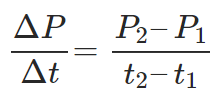
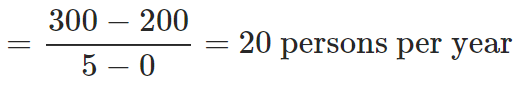
Question 2: Air is being pumped into a spherical balloon at a constant rate such that its radius increases constantly with respect to time according to the equation r(t) = 0.5t + r0(r is in cms and t is in minutes). Find the rate of change of its volume when its radius is 5 cm. Assume that the initial radius of the balloon is r=ocm. Answer with correct units.
Solution: Formula for volume of a sphere of radius r is: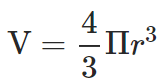
To find dV/dt, we can differentiate the expression for volume to get: 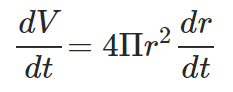
From the given information, we can get; dr/dt = 0.5cm/min. Using this value and r = 5cm in the expression for rate of change of volume, we finally have: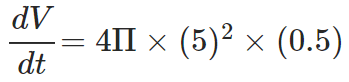
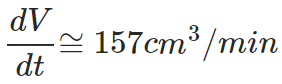
A Physical Example
Velocity and accelerationThis is a very crucial topic in the branch of Mechanics in physics. Given a particle has a position ‘x’ that depends on time ‘t’. Then the rate of change of the particle’s position ‘x’ with time ‘t’ is known as the velocity ‘v’ of the particle. This velocity may or may not depend on time according to the dependence of position on time.
Similarly, if the velocity ‘v’ has a time dependence; then the rate of change of the particle’s velocity ‘v’ with time ‘t’ is known as the acceleration ‘a’ of the particle. Thus, we have:
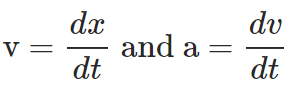
Let us solve a problem on this topic to clarify our concepts!
More Solved Examples for You
Question: A train moves along the railway track in such a way that the distance it covers, starting from the station A, is given by the equation x = 5t2 + t where x is in meters and t is in seconds. What would be the velocity and the acceleration of the train at time t = 25 seconds?
Solution: Given x(t) = 5t2 + t
To find: v(t = 25 sec) and a(t = 25 sec)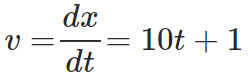
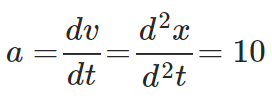
Now putting t = 25sec in the equations, we get v = 251 meters and a = 10 m/s2. Note that in this problem, the acceleration is independent of time. Such motion is said to be uniformly accelerated motion. This concludes the discussion on the Rate of Change of quantities.
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|

|
Explore Courses for JEE exam
|

|

















