Solved Examples: Union & Intersection of Sets | Applied Mathematics for Class 11 - Commerce PDF Download

Union of Sets

The Union of two sets A and B is the set of all the elements present in A or B or both. We will take the common elements at once only. It is denoted with the symbol “∪” read as “union”.
Symbolically,
A∪B = {x: x ∈A or x ∈B}

Union of two Joint Sets

If A and B are two finite sets and there is some common elements within them, that is, A∩B ≠ ∅
Then,
n (A∪B) =n (A) +n (B)-n (A∩B)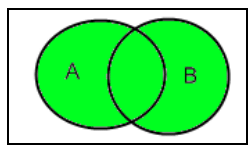

Union of two Disjoint Sets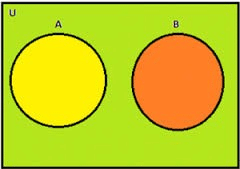

If A and B are two finite sets and there is no common elements within them, that is, A∩B = ∅
Then,
n (A∪B) = n (A) +n (B)

Intersection of Sets
The intersection of two sets A and B means a set of all the elements which are common to both A and B. It is represented by symbol “∩” reads as “Intersection”.
Symbolically,
A∩B = {x: x ∈ A and x ∈ B}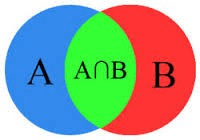

Difference of two Sets
The difference of two Sets A and B represents as A-B that is, all the element which are present in A but not in B.
Symbolically,
A – B = {x: x ∈ A and x ∉ B} and vice versa.
A-B is not necessarily equal to B-A
The above figure shows that the sets A – B, A ∩ B and B – A are disjoint sets, it means, the intersection of any of these two sets is the empty set that is, ∅
So,
n (A∪B) = n (A-B) + n (A∩B) + n (B-A)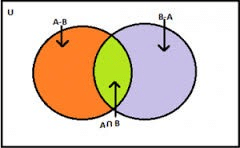

Union and Intersection of three Sets
If A, B and C are three finite joint sets, then their union will be, n (A ∪ B ∪ C) = n (A) + n (B) + n (C) - n (A ∩ B) – n (A ∩ C) - n (B ∩ C) + n (A ∩ B ∩ C)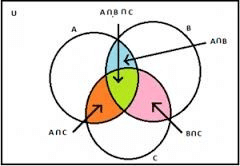

Complement of a Set
The complement of a set A is the set of all the elements which are the elements of Universal set but not the elements of A. It is represented by symbol A′ or A^c.
Symbolically,
A′ = {x: x U, x A}
A′=U-A
We must remember some properties of complement of sets to solve the problems related to it.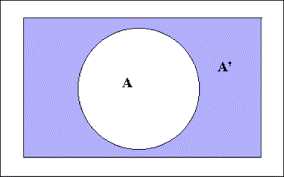

Properties of Complement of Sets are

• Difference Laws
  A-(B∪C) = (A-B) ∩ (A-C).
  A-(B∩C) = (A-B) ∪ (A-C)
• De Morgan’s Law
  (A ∪ B)′ = A′ ∩ B′
  (A ∩ B)′ = A′ ∪ B′

Problems related to Union and Intersection of Sets
Example 1: There are 500 students in a school, 220 like science subject, 180 like math and 40 like both science and math. Find the number of students who like

• Science but not math
• Math but not science
• Either math or science

Solution:
Let the total number of students be U that is, the universal set.
Let A is the set of number of students who like science.
Let B is the set of number of students who like math.
Here, n (U) =500      n (A) =220    n (B) =180    n (A∩B) =40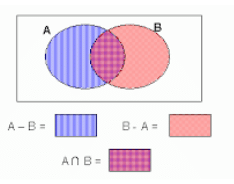

• Here we have to find the number of students who like science but not math, so symbolically we have to find A-B.
  As it is showing in the Venn diagram,
  A = (A-B) ∪ (A∩B)
  n (A) = n (A-B) + n (A∩B)
  n (A-B) = n (A) - n (A∩B)
  = 220 – 40 = 180
  Hence, the numbers of students who like science only not math are 180.
• Here we have to find the number of students who like math but not science, so symbolically we have to find B-A.
  B = (B-A) ∪ (A∩B)
  n (B) = n (B-A) +n (A∩B)
  n (B-A) =n (B)-n (A∩B)
  =180 - 40 = 140
  Hence, the numbers of students who like math only not science are 140.
• Here we have to find the number of students who like either math or science.
  n (A∪B) = n (A) + n (B) – n (A∩B)
  = 220 + 180 – 40
  = 360

Example 2: In a college, there are 20 students who enrolled for commerce only,90 students enrolled for mathematics only, 30 students enrolled for commerce and mathematics both and 60 students enrolled for others. Find

• The total number of students in college
• Total number of students enrolled either for commerce or mathematics
• Total number of students enrolled for commerce
• Total number of students enrolled for mathematics

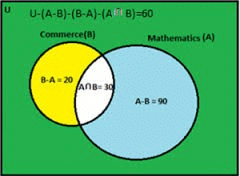
Solution:
Given in the Venn diagram,
Let total number of students as U
Students of Commerce as B
Students of Mathematics as A
B – A = 20        A – B = 90           A∩B = 30

• As it is given in Venn diagram,
  n (U)-n (A-B)-n (B-A)-n (A∩B) = 60
  n (U) = 60+ n (A-B) + n (B-A) + n (A∩B)
  = 60 + 90 + 20 + 30
  = 200
  Hence there are total 200 students in college.
• n(A∪B) = n(A-B) + n(A∩B) + n(B-A) that is, the formula of difference of sets
  = 90 + 30 + 20
  = 140
  Hence there are 140 students who enrolled either for commerce or mathematics.
• n(B) = n(B-A) + n(A∩B)
  = 20 + 30
  = 50
  Hence there are 50 students who enrolled for commerce.
• n(A) = n(A-B) + n(A∩B)
  = 90 + 30
  = 120
  Hence there are 120 students who enrolled for mathematics.

Example 3: In a shop, 380 people buy socks, 150 people buy shoes and 200 people buy belt. If there are total 580 people who bought either socks or shoes or belt and only 30 people bought all the three things? So how many people bought exactly two things.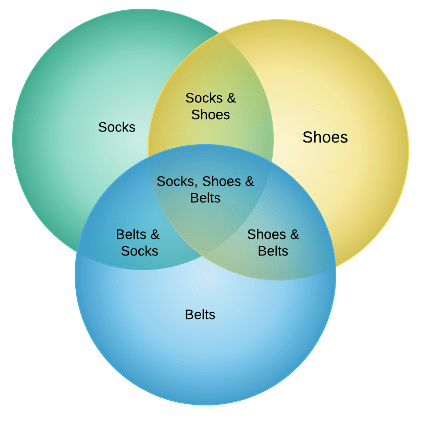

Solution:
Let S, H and B represent the set of number of people bought socks, shoes and belt respectively.
So, n(S) = 380, n (H) = 150, n (B) = 200
n (S∪H∪B) =580, n (S∩H∩B) =30
Therefore, n (S ∪ H ∪ B ) = n ( S ) + n ( H )+ n ( B ) – n (S ∩ H ) – n (H ∩ B ) – n (B ∩ S ) +  n ( S ∩ H ∩ B ),
Now, we will put values given in the formula,
580 = 380 + 150 + 200 - n (S ∩ H) – n (H ∩ B) – n (B ∩ S) + 30
This gives that,
n (S ∩ H) + n (H ∩ B) + n (B ∩ S) =180
But this includes the number of people who bought all the three items also. So we have to deduct these numbers of people from it.
Let, n (S ∩ H ∩ B) = a
As we can see from the Venn diagram,
n (S ∩ H)-a + n (H ∩ B)-a + n (B ∩ S)-a=the required number
n (S ∩ H) + n (H ∩ B) + n (B ∩ S)-3a
180 – 90 = 90
Hence, 90 people are there who bought exactly two things.

Example 4: In a school there are 25 teachers who teach engineering or management. Of these, 15 teach engineering and 6 teach both engineering and management. How many teach management?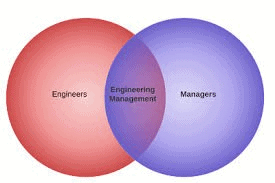

Solution:
Let M be the set of teachers who teach management and E be the set of teachers who teach engineering. Here ‘or’ means union and ‘and’ means intersection. So, we have
n (E ∪ M) = 25 , n (E) = 15 and n (E ∩ M) = 6
We have to calculate n (M).
According to formula
n (E ∪ M) = n (E) + n (M) – n (E∩ M),
We obtain
25 = 15 + n (M) – 6
Thus n (M) = 16
Hence 16 teachers teach management.

Example 5: If there are 400 elements in consideration, set A has 100 elements, set B has 150 elments, and 75 are the common elements. Find how many elements is neither in A nor in B.Draw the Venn diagram for supporting your answer.
Solution: 
Let U denote the set of total elements.
Given
n (U) = 400, n (A) = 100, n (B) = 150 and n (A ∩ B) = 75.
We have to calculate the elements which are neither in A nor in B and according to the De Morgan’s law of complement law, we know that
n (A′ ∩ B′) = n (A ∪ B)′
= n (U) – n (A ∪ B) i.e. the complement of any set is U –A and here we have to calculate the complement of the union of A and B so
n (A ∪ B)′= n (U) – n (A ∪ B)
= n (U) – n (A) – n (B) + n (A ∩ B)
= 400 – 100 – 150 + 75 = 225
Hence the number of elements neither in A nor in B are 225.
The Venn diagram of the n (A ∪ B)′ is shown on the right figure: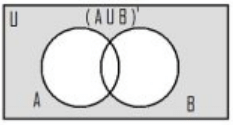

Example 6: There was an investigation of 500 families having pet.400 were having dog as pet and 200 were have cat as pet, 50 owned both cat and dog as pet. Now find if this data is correct? Justify your answer.
Solution: 
Let U be the set of families investigated, D be the set of families having dog as pet and C be the set of families having cat as a pet.
Given,
n (U) = 500, n (D) = 400, n (C) = 200 and n (D ∩ C) = 50.
Now we will put the values in the formula of union of two sets.
n (D ∪ C) = n (D) + n (C) – n (D ∩ C)
= 200 + 400 – 50
= 550
Here the union of two sets is 550 and the total numbers of families investigated are 500.
D ∪ C ⊂ U implies n (D ∪ C) ≤ n (U).
The union of two sets should be the subset of universal set that is, it should be less than or equal to universal set.
As there is a contradiction, so, the given data is incorrect.