Acceleration Due to Gravity of the Earth | Physics Class 11 - NEET PDF Download
What is Acceleration due to Gravity?
Acceleration due to gravity is the acceleration gained by an object due to gravitational force. Its SI unit is m/s2. It has both magnitude and direction, hence, it’s a vector quantity. Acceleration due to gravity is represented by g. The standard value of g on the surface of the earth at sea level is 9.8 m/s2.
Acceleration due to Gravity – Formula, Unit and Values
Acceleration Due to Gravity (g) | |
Symbol | g |
Dimensional Formula | M0L1T-2 |
SI Unit | ms-2 |
Formula | g = GM/r2 |
Values of g in SI | 9.806 ms-2 |
Values of g in CGS | 980 cm s-2 |
What is Gravity?
Gravity is the force with which the earth attracts a body towards its centre. Let us consider two bodies of masses ma and mb. Under the application of equal forces on two bodies, the force in terms of mass is given by:
mb = ma [aA/aB] this is called an inertial mass of a body.
Under the gravitational influence on two bodies,
- FA = GMmA/r2,
- FB = GMmB/r2,
- mB = [FB/FA] × mA
The above mass is called a gravitational mass of a body. According to the principle of equivalence, the inertial mass and gravitational mass are identical. We will be using this while deriving acceleration due to the gravity given below.
Let us suppose a body [test mass (m)] is dropped from a height ‘h’ above the surface of the earth [source mass (M)], it begins to move downwards with an increase in velocity as it reaches close to the earth surface. We know that velocity of an object changes only under the action of a force, in this case, the force is provided by the gravity. Under the action of gravitational force, the body begins to accelerate toward the earth’s centre which is at a distance ‘r’ from the test mass.
Then, ma = GMm/r2 (Applying principle of equivalence)
⇒ a = GM/r2 . . . . . . . (1)
The above acceleration is due to the gravitational pull of earth so we call it acceleration due to gravity, it does not depend upon the test mass. Its value near the surface of the earth is 9.8 ms-2.
Therefore, the acceleration due to gravity (g) is given by = GM/r2.
Formula of Acceleration due to Gravity
Force acting on a body due to gravity is given by, f = mg
Where f is the force acting on the body, g is the acceleration due to gravity, m is mass of the body.
According to the universal law of gravitation, f = GmM/(r+h)2
Where,
- f = force between two bodies,
- G = universal gravitational constant (6.67×10-11 Nm2/kg2)
- m = mass of the object,
- M = mass of the earth,
- r = radius of the earth.
- h = height at which the body is from the surface of the earth.
As the height (h) is negligibly small compared to the radius of the earth we re-frame the equation as follows, f = GmM/r2
Now equating both the expressions,
mg = GmM/r2
⇒ g = GM/r2
Therefore, the formula of acceleration due to gravity is given by, g = GM/r2
Note: It depends on the mass and radius of the earth.
This helps us understand the following:
- All bodies experience the same acceleration due to gravity, irrespective of its mass.
- Its value on earth depends upon the mass of the earth and not the mass of the object.
Acceleration due to Gravity on the Surface of Earth
Earth as assumed to be a uniform solid sphere with a mean density. We know that,
Density = mass/volume
Then, ρ = M/[4/3 πR3]
⇒ M = ρ × [4/3 πR3]
We know that, g = GM/R2.
On substituting the values of M we get,
g = 4/3 [πρRG]
At any distance ‘r’ from the centre of the earth
g = 4/3 [πρRG]
The value of acceleration due to gravity ‘g’ is affected by
- Altitude above the earth’s surface.
- Depth below the earth’s surface.
- The shape of the earth.
- Rotational motion of the earth.
Variation of g with Height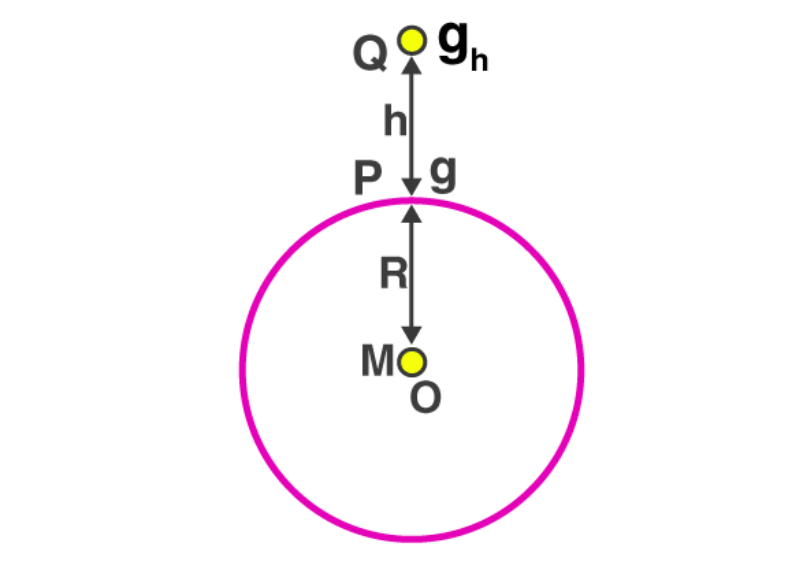
Acceleration due to Gravity at a height (h) from the surface of the earth
Consider a test mass (m) at a height (h) from the surface of the earth. Now, the force acting on the test mass due to gravity is;
F = GMm/(R+h)2
Where M is the mass of earth and R is the radius of the earth. The acceleration due to gravity at a certain height is ‘h’ then,
mgh= GMm/(R+h)2
⇒ gh= GM/[R2(1+ h/R)2 ] . . . . . . (2)
The acceleration due to gravity on the surface of the earth is given by;
g = GM/R2 . . . . . . . . . (3)
On dividing equation (3) and (2) we get,
gh = g (1+h/R)-2. . . . . . (4)
This is the acceleration due to gravity at a height above the surface of the earth. Observing the above formula we can say that the value of g decreases with increase in height of an object and the value of g becomes zero at infinite distance from the earth.
Approximation Formula:
From Equation (4)
when h << R, the value of g at height ‘h’ is given by gh = g/(1 – 2h/R)
Variation of g with Depth
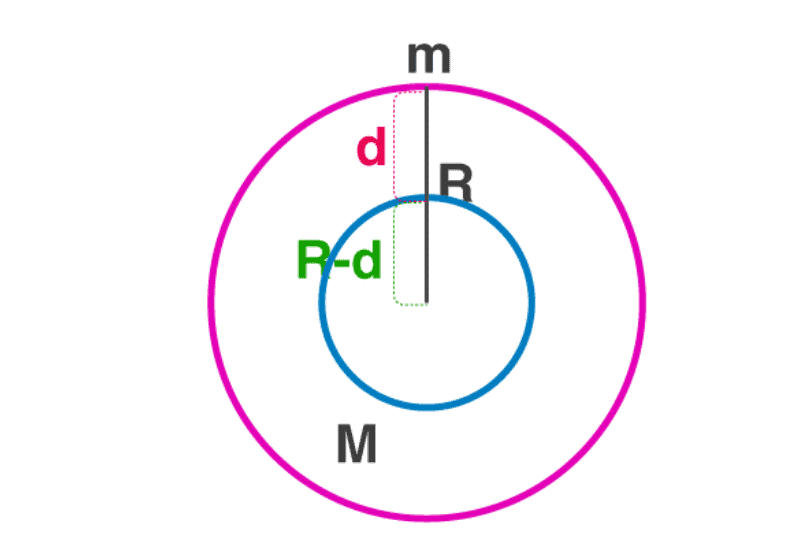
Consider a test mass (m) taken to a distance (d) below the earth’s surface, the acceleration due to gravity that point (gd) is obtained by taking the value of g in terms of density.
On the surface of the earth, the value of g is given by;
g = 4/3 × πρRG
At a distance (d) below the earth’s surface, the acceleration due to gravity is given by;
gd = 4/3 × πρ × (R – d) G
On dividing the above equations we get,
gd = g (R – d)/R
- When the depth d = 0, the value of g on the surface of the earth gd = g.
- When the depth d = R, the value of g at the centre of the earth gd = 0.
Variation of g due to Shape of Earth
As the earth is an oblate spheroid, its radius near the equator is more than its radius near poles. Since for a source mass, the acceleration due to gravity is inversely proportional to the square of the radius of the earth, it varies with latitude due to the shape of the earth.
gp/ge = R2e/R2p
Where ge and gp are the accelerations due to gravity at equator and poles, Re and Rp are the radii of earth near equator and poles, respectively.
From the above equation, it is clear that acceleration due to gravity is more at poles and less at the equator. So if a person moves from the equator to poles his weight decreases as the value of g decreases.
Variation of g due to Rotation of Earth
Consider a test mass (m) is on a latitude making an angle with the equator. As we have studied, when a body is under rotation every particle in the body makes circular motions about the axis of rotation. In the present case, the earth is under rotation with a constant angular velocity ω, then the test mass moves in a circular path of radius ‘r’ with an angular velocity ω.
This is the case of a non-inertial frame of reference so there exists a centrifugal force on the test mass (mrω2). Gravity is acting on the test mass towards the centre of the earth (mg).
As both these forces are acting from the same point these are known as co-initial forces and as they lie along the same plane they are termed as co-planar forces.
We know from parallelogram law of vectors, if two coplanar vectors are forming two sides of a parallelogram then the resultant of those two vectors will always along the diagonal of the parallelogram.
Applying parallelogram law of vectors we get the magnitude of the apparent value of the gravitational force at the latitude
(mg′)2 = (mg)2 + (mrω2)2 + 2(mg) (mrω2) cos(180 – θ) . . . . . . (1)
We know ‘r’ is the radius of the circular path and ‘R’ is the radius of the earth, then r = Rcosθ.
Substituting r = R cosθ we get,
g′ = g – Rω2cos2θ
Where g′ is the apparent value of acceleration due to gravity at the latitude due to the rotation of the earth and g is the true value of gravity at the latitude without considering the rotation of the earth.
At poles, θ = 90°⇒ g’ = g.
At the equator, θ = 0° ⇒ g′= g – Rω2.
Important Conclusions on Acceleration due to Gravity
- For an object placed at a height h, the acceleration due to gravity is less as compared to that placed on the surface.
- As depth increases, the value of acceleration due to gravity (g) falls.
- The value of g is more at poles and less at the equator.
|
96 videos|367 docs|98 tests
|
FAQs on Acceleration Due to Gravity of the Earth - Physics Class 11 - NEET
| 1. What is acceleration due to gravity? |  |
| 2. How is acceleration due to gravity calculated? |  |
| 3. Does the acceleration due to gravity vary with location on Earth? |  |
| 4. How does altitude affect the acceleration due to gravity? |  |
| 5. Does the acceleration due to gravity change with the mass of an object? |  |
















