Solved Examples for JEE: Limits & Derivatives | Mathematics (Maths) for JEE Main & Advanced PDF Download

What is a Limit in calculus? A limit can be explained as the value which a function tends to approach as the input value (which is also known as index) gains some value. It is the converging of different values at a point. Boundedness of a function is shown by limits. In this article we come across limits solved examples.
Consider f(x) to be a function. In a function, if x takes a definite value say b, x → b is called limit. Here ‘b’ is a value which is pre-assigned. It is represented as lim_x→bf(x). 

The tendency of f(x) at x=a towards the left is called left limit and denote by lim_x→a^– and towards the right is called right limit denoted by lim_x→a⁺. Limit of a function at a point is the common value of the right and left hand limits, if they coincide.
The graphical representation of limits is as follows:

Algebra of limits

Suppose lim_x→a a(x) = r and lim_x→a b(x) = t then the following can be defined.

• lim_x→a [r(x) + t(x)] = lim_x→a r(x) + lim_x→a t(x).
• lim_x→a [r(x) − t(x)] = lim_x→a r(x) − lim_x→a t(x).
• lim_x→a [r(x) × t(x)] = [lim_x→a r(x)] × [lim_x→a t(x)].
• lim_x→a [r(x) ÷ t(x)] = [lim_x→a r(x)] ÷ [lim_x→a t(x)].
• lim_x→a [α.r(x))] = α. lim_x→a r(x).

Some Standard Limits

The following are some of the standard limits.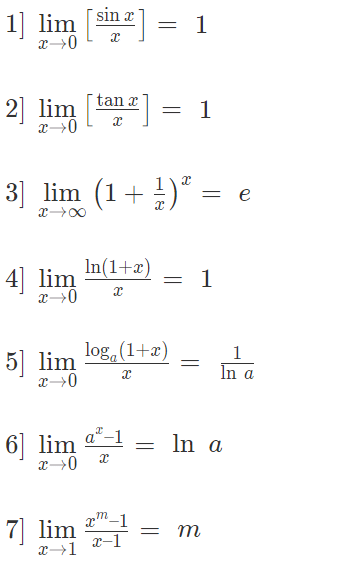

Solved Practice Examples on Limits

Below are illustrated some of the examples based on limits asked questions in JEE previous exams.
Example 1: Find lim_x→∞ sinx/x.
Solution:
Let x = 1/y or y = 1/x, so that x → ∞ ⇒ y → 0
∴ lim_x→∞ (sin x / x) = lim_y→0 (y . sin (1 / y))
= lim_y→0  y . lim_y→0 sin (1 / y)
= 0

Example 2: If f(a) = 2, f′(a) = 1, g(a) = −1; g′(a) = 2, then find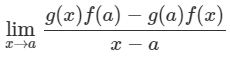

Solution: Consider





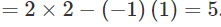
Example 3: Evaluate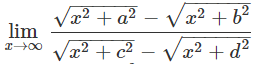

Solution: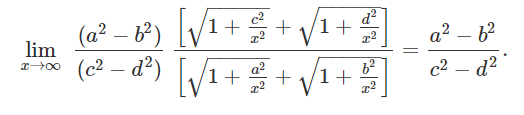


Example 4: Find the limit lim_n→∞ [1/n² + 2/n² + … + n/n²]
Solution:
lim_n→∞ [1/n² + 2/n² + … + n/n²]
= lim_n→∞ [1+2+3+…. +n]/ n²
= lim_n→∞ [(n / 2) * ( n+1)] / n²
= ½ lim_n→∞ ( n+1) / n
= ½ lim_n→∞ (1 + 1/n)
= -½

Example 5: Find lim_x→0 sin (π cos²x) / x²
Solution:

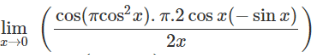
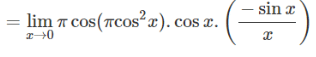
= π (-1).1.(-1) = π

Example 6: let f: R→R be such that f (1) = 3 and f’(1) = 6. Then find the value of lim _x→0 [f (1+x) / f (1)]^1/x.
Solution:
Let y = [f (1 + x) / f (1)]^1/x
So, log y = 1/x [log f (1 + x) – log f (1)]
So, lim_x→0 log y = lim_x→0 [1 / f (1 + x) . f’(1 + x)]
= f’(1) / f(1)
= 6/3
log (lim_x→0 y) = 2
lim_x→0 y = e²

Example 7: If f (x) = [2/x ] − 3, g (x) = x − [3 / x] + 4 and h (x) = −[2 (2x + 1)] / [x² + x − 12], then what is the value of lim_x→3 [f (x) + g (x) + h (x)]?
Solution:
We have f (x) + g (x) + h (x) = [x² − 4x + 17− 4x − 2] / [x² + x − 12]
= [x² − 8x + 15] / [x² + x − 12]
= [(x − 3) (x − 5)] / [(x − 3) (x + 4)]
∴ lim_x→3 [f (x) + g (x) + h (x)] = lim_x→3 (x − 3) (x − 5) / (x − 3) (x + 4)
= −2/7

Practice the following important questions in class 11 Maths Limits and Derivatives that should help you to solve the problems faster with accuracy.
Question 1: Find the derivative of the function x²cos x.
Solution:
Given function is x²cos x
Let y = x²cos x
Differentiate with respect to x on both sides.
Then, we get:
dy/dx = (d/dx)x²cos x
Now, using the formula, we can write the above form as:
dy/dx = x² (d/dx) cos x + cos x (d/dx)x²
Now, differentiate the function:
dy/dx = x² (-sin x) + cos x (2x)
Now, rearrange the terms, we will get:
dy/dx = 2x cos x – x² sin x

Question 2: Find the positive integer “n” so that lim_{x → 3}[(xⁿ– 3ⁿ)/(x – 3)] = 108.
Solution:
Given limit: lim_{x → 3}[(xⁿ– 3ⁿ)/(x – 3)] = 108
Now, we have:
lim_{x → 3}[(xⁿ– 3ⁿ)/(x-3)] = n(3)^n-1
n(3)^n-1 = 108
Now, this can be written as:
n(3)^n-1 = 4 (27) = 4(3)^4-1
Therefore, by comparing the exponents in the above equation, we get:
n = 4
Therefore, the value of positive integer “n” is 4.

Question 3: Find the derivative of f(x) = x³ using the first principle.
Solution:
By definition,
f’(x) = lim_{h→ 0} [f(x+h)-f(x)]/h
Now, substitute f(x)=x³ in the above equation:
f’(x) = lim_{h→ 0} [(x+h)³-x³]/h
f’(x) = lim_{h→ 0} (x³+h³+3xh(x+h)-x³)/h
f’(x) = lim_{h→ 0} (h²+3x(x+h))
Substitute h = 0, we get:
f’(x) = 3x²
Therefore, the derivative of the function f’(x) = x³ is 3x².

Question 4: Determine the derivative of cosx/(1+sin x).
Solution:
Given function: cosx/(1+sin x)
Let y = cosx/(1+sin x)
Now, differentiate the function with respect to “x”, we get
dy/dx = (d/dx) (cos x/(1+sin x))
Now, use the u/v formula in the above form, we get
dy/dx = [(1+sin x)(-sin x) – (cos x)(cos x)]/(1+sin x)²
dy/dx = (-sin x – sin²x-cos²x)/(1+sin x)²
Now, take (-) outside from the numerator, we get:
dy/dx = -(sin x + sin^2.x + cos²x)/(1+sin x)²
We know that sin^2.x + cos²x = 1
By substituting this, we can get:
dy/dx = -(1+sin x)/(1+sin x)²
Cancel out (1+sin x) from both numerator and denominator, we get:
dy/dx = -1/(1+sin x)
Therefore, the derivative of cosx/(1+sin x) is -1/(1+sin x).

Question 5: lim_{x→ 0} |x|/x is equal to:
(a) 1
(b) -1
(c) 0
(d) does not exists
Ans: (d)
Explanation:
The limit mentioned here is x→0
It has two possibilities:
Case 1: x→0⁺
Now, substitute the limit in the given function:
lim_{x→ 0+} |x|/x = x/x = 1
Case 2: x→0^–
Now, substitute the limit in the given function:
lim_{x→ 0-} |x|/x = -x/x = -1
Hence, the result for both cases varies, the solution is an option (D)

Question 6: Evaluate the derivative of f(x) = sin²x using Leibnitz product rule.
Solution:
Given function: f(x) = sin²x
Let y= sin²x
Now, by using Leibnitz product rule, we can write it as:
dy/dx = (d/dx) sin²x
Sin²x can be written as (sin x)(sin x)
Now, it becomes:
dy/dx = (d/dx) (sin x)(sin x)
dy/dx = (sin x)’(sin x) + (sin x)(sin x)’
dy/dx = cos x sin x + sin x cos x
dy/dx = 2 sin x cos x
dy/dx = sin 2x
Therefore, the derivative of the function sin²x is sin 2x.

Solve chapter limits and derivatives important problems given below:

• Evaluate: lim_{x → 0} [(sin²2x)/(sin²4x)]
• Differentiate the function with respect to x: (ax² + cot x)(p+q cos x)
• Show that the lim_{x → 0} [(|x-4|)/(x-4)] does not exists
• Evaluate the following:
  lim_{y → 0} [(x+y)sec(x+y)-x sec x]/y
• Differentiate 1/(ax²+bx+c) with respect to x.
• Evaluate the derivative of 99x at x=100
• Find the derivative of the following trigonometric functions:
  (i) 2 tan x – 7 sec x
  (ii) sin x cos x
  (iii) 5 sec x + 4 cos x
• Differentiate the function: cos (x²+1).
• Differentiate x² sin x + cos 2 x.
• Differentiate (2x – 7)² (3x+5)³.