Reducing Equations to Simpler Form | Advance Learner Course: Mathematics (Maths) Class 7 PDF Download
Reducing equations is a method of solving a complex equation and writing the equation into a simpler form. Not all the equations are in the form of linear equations( A linear equation is an equation of the first order.) but they can be solved by putting them into the form of linear equation by performing some mathematical operations on them like cross-multiplication. After reducing these non-linear equations in linear form they can be solved and the value of the variable can be calculated easily.
Steps for Reducing Equations To Simpler Form
1. If the given equation is in non-linear form, so it cannot be directly solved. Therefore, first we will need to simplify the given equation by using the Cross Multiplication technique.
2. Cross multiply both sides of the equation i.e. the denominator on one sides is multiplied to the numerator on the other side.
3. Use the distributive law to open the brackets.
4. Bring all the variables on one side (LHS) and constants on other side of the equation (RHS)
5. Solve the rest of the equation as linear equation in one variable.
x – y / y = y – x / x
Step 1: Doing cross multiplication we get:
x (x – y) = y (y – x)
x2 – xy = y2 – xy
Step 2: Bring all the x variables on one side i.e. LHS and all the y variable on the other side i.e. RHS
x2 – xy + xy = y2
x2 = y2
Step 3: Taking square root on both the side we get,
x = y
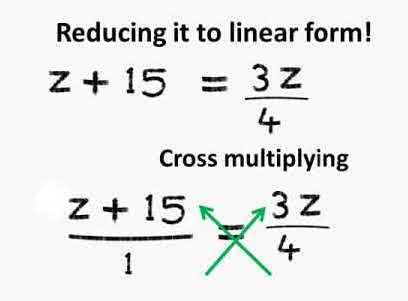 Example of reducing the equation to linear formLet us now take some examples to understand the method of reducing equations in simpler form.
Example of reducing the equation to linear formLet us now take some examples to understand the method of reducing equations in simpler form.
Example 1. x – 1 / x + 2 = 1 / 6
Solution:
Step 1: As the equation is in non-linear form, so this cannot be directly solved. Therefore, first we will need to simplify the given equation by using the Cross Multiplication technique.
x – 1 / x + 2 = 1 / 6
Cross Multiplication technique : The denominator on both sides are multiplied to the numerator on the other side.
Step 2: After cross multiplication, the equation can be written as:
6 (x – 1) = 1 (x + 2)
Step 3: Now open the parentheses by using distributive law
6x – 6 = x + 2
Step 4: Bring all the variables on one side i.e. LHS and all the constants on the other side i.e. RHS
6x – x = 2 + 6
5x = 8
Step 5: Dividing both the sides by 5
x = 8/5
Example 2. 2x – 3 / 2x + 2 = 1 / 6
Solution:
= 2x – 3 / 2x + 2 = 1 / 6 [simplifying the given equation by using the Cross Multiplication technique]
= 6 (2x – 3) = 1 (2x + 2)
= 12x – 18 = 2x + 2 [using distributive law]
= 12x – 2x = 2 + 18
= 10x = 20
= x = 2 [Dividing both the sides by 10]
Example 3. x/2 – 1/5 = x/3 + 1/4
Solution:
As the given equation is in the complex form, we have to reduce it into a simpler form.
= Take the L.C.M. of the denominators 2, 5, 3 and 4 which is 60.
= x * 60 / 2 – 1 60 / 5 = x * 60 /3 + 1 * 60 /4 [Multiply both the sides by 60]
= 30x −12 = 20x + 15
= 30x − 20x = 15 + 12
= 10x = 27
= x = 2.7 [Dividing both the sides by 10]
Example 4. x – 1 = x/3 + 3/4
Solution:
= Take the L.C.M. of the denominators 3 and 4 which is 12.
= x * 12 – 1 * 12 = x * 12 /3 + 3 * 12 /4 [Multiply both the sides by 12]
= 12x −12 = 4x + 9
= 12x − 4x = 9 + 12
= 8x = 31
= x = 31/8 [Dividing both the sides by 8]
|
41 videos|45 docs|9 tests
|
FAQs on Reducing Equations to Simpler Form - Advance Learner Course: Mathematics (Maths) Class 7
| 1. How can I reduce an equation to a simpler form? |  |
| 2. What are the steps for reducing an equation to its simplest form? |  |
| 3. Are there any specific techniques for reducing complex equations? |  |
| 4. Can you provide an example of reducing an equation to a simpler form? |  |
| 5. Can reducing an equation to a simpler form help in solving real-life problems? |  |
















