What are Fractions? | Additional Study Material for Class 6 PDF Download

The word fraction is derived from the Latin word "fractio" which means 'to break'. The Egyptians, being the earliest civilization to study fractions, learnt fractions to resolve their mathematical problems, which included the division of food, supplies and the absence of a bullion currency.
In Ancient Rome, fractions were only written using words to describe a part of the whole. In India, the fractions were first written with one number above another (numerator and denominator), but without a line. It was the Arabs only, who added the line which is used to separate the numerator and the denominator.

What are Fractions?

In Mathematics, fractions are represented as a numerical value, can be defined as the parts of a whole. A fraction can be a portion or section of any quantity out of a whole, where, the whole can be any number, a  specific value, or a thing. Let us understand this concept using an example. Here's a pizza that is divided into 8 equal parts. Do you know what 1/8 means?

It means one in eight equal parts. It can also be read as:

• One-eighth, or
• 1 by 8

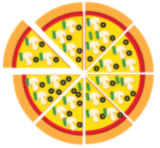1/8 fraction

This is called a fraction.

Parts of a Fraction

All fractions consist of a numerator and a denominator.

• The denominator indicates how many parts the whole has been divided into. It is placed in the lower part of the fraction.
• The numerator indicates how many sections of the fraction are represented. It is placed in the upper part of the whole.

Types of Fractions

Based on numerator and denominator, which are parts of a fraction, there are different types of fractions and those are listed below:

1. Proper Fraction: Proper fractions are the fractions in which the numerator is less than its denominator. It is often smaller than the whole. Example: 5/7, 3/8, 2/5, etc.
2. Improper Fraction: An Improper fraction is the type of fraction in which the numerator is more than or equal to its denominator. It is always the same or greater than the whole. Example: 4/3, 5/2, 8/5, etc.
3. Unit Fraction: Fractions with numerator as 1 are known as unit fractions. Example: 1/4, 1/7, 1/9, etc.
4. Mixed Fraction: A mixed fraction is a mixture of a whole and a proper fraction. Example: 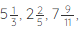etc.
5. Equivalent Fraction: Equivalent fractions are the fractions that represent the same value. It's the same portion of a whole. To get equivalent fractions of any given fraction:
   - We can multiply both the numerator as well as the denominator of the given fraction by the same number.
   - And for division, we can divide both the numerator and the denominator of the given fraction by the same number.

Example: Find the two fractions equivalent to 5/7.
Solution: Equivalent Fraction 1: 5/7= 5/7 x 2/2 = 10/14
Equivalent Fraction 2: 5/7 = 5/7 x 3/3 = 15/21

Like and Unlike Fractions

Like fractions are the fractions that have the same denominators. Example: 5/15, 3/15, 17/15, and 31/15.
Unlike fractions are the fractions which have different denominators. Example: 2/7, 9/11, 3/13, and 39/46.

Fractions on a Number Line

The representation of fractions on a number line demonstrates the intervals between two integers, which also show us the fundamental principle of fractional number creation.
Example: Let's represent the fractions: 2/11, 7/11, -8/11, and -3/11 on a number line.
Solution: Since the denominator of each given fraction is 11, we can divide the space between every pair of two consecutive integers (on the number line) into 11 equal parts.

Each part will represent the fraction 1/11 on the number line. 

• To mark 2/11, move two parts to the right of zero.
• To mark 7/11, move seven parts to the right of zero.
• To mark -8/11, move eight parts to the left of zero.
• To mark -3/11, move three parts to the left of zero.

Hence, the markings of fractions on the number line will be in the sequence: -8/11, -3/11, 2/11, and 7/11.
Fractions on Number Line Note: The markings on the number line are just for showing the order of fractions. These are not the actual number gaps.

Solved Examples

Example 1: Milk is sold at $16 per gallon. Find the cost of 6(2/5) gallons of milk.
Solution: Cost of one gallon of milk = $16
Therefore, the cost of 6(2/5) gallons i.e. 32/5 gallons will be 32/5 * 16 = $102.4
Therefore, the cost of gallons of milk is $102.4

Example 2: In a class of 48 students, 1/4 of them watch cartoons. How many students do not watch cartoons?
Solution: Total number of students = 48
Number of students who watch cartoons = 1/4 x 48 = 12
Thus, the number of students who don't watch cartoons = 48 - 12 = 36
Therefore, the number of students who do not watch cartoons is 36

Example 3: The snowfall during the first three months in winter was 30.5 inches, 45.25 inches, and 25.25 inches. What was the total amount of snow in these months?
Solution: Total amount of snow for three months = 30.5 + 45.25 + 25.25
= 305/10 + 452.5/10 + 252.5/10
= (305 + 452.5 + 252.5)/10 = 1010
=1010/10 = 101inches
Therefore, the total amount of snow in 3 months was 101 inches.

Comparing Fractions

How to Compare Fractions?

Before exploring the concept of comparing fractions, let us recall fractions. A fraction is nothing but a part of a whole thing. If you break a glass dish into several pieces, can you still say that each part represents a fraction? Yes, reasonably each part can still be called a fraction of the glass dish, but in math, a fraction comes with a rule. The rule is "each of the parts has to be equal." A fraction has two parts; they are called numerator and denominator.
Now, let's discuss what comparing fractions mean. When the two fractions are compared to find out which is greater or which is smaller. The real-time examples of comparing fractions include a number of activities, splitting a bill, following a recipe, checking discounted prices while shopping, comparing sales of a particular product, medical prescriptions by the doctor, scores of tests and exams, etc. Let us go through the different methods of comparing fractions with the help of examples to understand the concept better.

Comparing Fractions with Same Denominators

In this method, we check the denominators to see if they are the same. If the denominators are the same, then the fraction with the bigger numerator is the bigger fraction and the fraction with the smaller numerator is the smaller fraction. If both numerators and denominators are equal, the fractions are also equal. For example, let us compare 6/17 and 16/17

• Step 1: Look for denominators of the given fractions:6/17 and 16/17. Denominators are the same.
• Step 2: Compare numerators. 16>6.
• Step 3: The fraction with a larger numerator would be a larger fraction. Therefore, 6/17 < 16/17.

Comparing Fractions with Unlike Denominators

For comparing fractions with unlike denominators, start by finding the least common denominator(LCM) to make the denominators the same. When the denominators are made the same, the fraction with the larger numerator is the larger fraction. For example 1/2 and 2/5.

• Step 1: Look for denominators of the given fractions: 1/2 and 2/5. Denominators are not same.
• Step 2: Take LCM of 2 & 5. LCM(2, 5) = 10.
• Step 3: 1/2 = 1/2 × 5/5 and 2/5 = 2/5 × 2/2.
• Step 4: Compare fractions: 5/10 and 4/10. Denominators are the same. Compare numerators, 5>4
• Step 5: 5/10 > 4/10. The fraction with a larger numerator would be a larger fraction. Thus, 5/10 > 4/10. Therefore, 1/2  > 2/5

Also, if the denominators are different and the numerators are the same, then we can easily compare fractions by looking at their denominators. The fraction with a smaller denominator has a greater value and the fraction with a larger denominator has a smaller value. For example, 2/3 > 2/6.

Decimal Method of Comparing Fractions

In this method, we compare the decimal values of fractions. For this, the numerator is divided by the denominator and the fraction is converted into a decimal. Then, the decimal values are compared. For example, 4/5 and 6/8.

• Step 1: Write 4/5 and 6/8 in decimals. 4/5 = 0.8 and 6/8 = 0.75.
• Step 2: Compare decimal values. 0.8 > 0.75
• Step 3: The fraction with a larger decimal value would be a larger fraction. Therefore, 4/5 > 6/8

Comparing Fractions Using Visualization

We can use various graphical methods and models to visualize larger fractions. Model A and B represent the given respective fractions. 4/8 < 4/6 because 4/6 covers a larger shaded area than 4/8. Note that the smaller fraction occupies a lesser area of the same whole. A point to be taken into consideration here is that the size of models A and B should be exactly the same for the comparison to be valid. Each model is then divided into equal parts equivalent to their respective denominators.

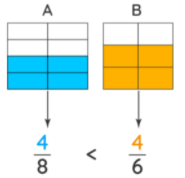
Comparing Fractions Using Cross Multiplication

In this method, we cross multiply the numerator of one fraction with the denominator of the other fraction. The same has been indicated by the arrows in the figure below. In the example given below, when we cross multiply, we get 4 and 6. 4 and 6 are the numerators we would get if we expressed 1/2 and 3/4 with the common denominator 8. The new fractions with the same denominators will be 4/8 and 6/8. Since 6 is a greater numerator, 4/8 < 6/8. Therefore, 1/2 < 3/4

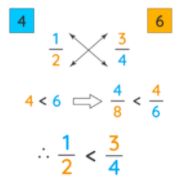
Important Points
The common methods used to compare fractions are:

• Decimal method
• Cross-multiplication method
• Graphical/Visual method
• LCM method to make the denominators the same

Solved Examples

Example 1: Nathan is confused and asks why is 5/11 > 4/11? Can you explain it to him?
Solution: 5/11 and 4/11 have the same denominators; hence, we can simply compare the fractions by observing the numerators. The fraction with a greater numerator will be a greater fraction. 5 > 4. Therefore, 5/11 > 4/11.

Example 2: Ryan was asked to prove that the given fractions: 4/6 and 6/9 are the same using the LCM method. He is a bit confused. Can you help him?
Solution: In this method, we find lcm of the denominators of the given fractions, making the denominator the same. By doing so, we get 18 for both. 12 will be the numerator if we expressed 4/6 and 6/9 with the common denominator 18 (LCM of both the denominators). The new fractions with the same denominators will be 12/18 and 12/18. Hence, both the fractions are equal: 4/6 = 6/9. Therefore, 4/6 = 6/9.

Addition and Subtraction of Fractions

Introduction to Fractions

Fractions are part of a whole. We can apply basic arithmetic operations on fractions. Hence, it is possible to add, subtract, multiply and divide the fractions. Before moving to the addition of fractions, let us revise about fractions here.

Adding and Subtracting Fractions with Like Denominators

Adding Fractions with Like Denominators

Let us add the fractions 15 and 25 using rectangular models. In this case, both the fractions have the same denominators. These fractions are called like fractions. The following figure represents both the fractions in the same model.

• 1/5 indicates that 1 out of 5 parts are shaded yellow.
• 2/5 indicates that 2 out of 5 parts are shaded green.

Out of the 5 parts, 3 parts are shaded. In the fractional form, this can be represented as 3/5.

Adding fractions with like denominators is simple:

• Add the numerators of the given fractions.
• Retain the same denominator.

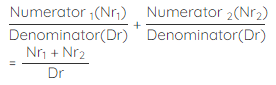
Now, let us see how to add the above fractions using this formula.
2+1/5 = 35
It should be noted that we use the same method for subtracting fractions.

Subtracting Fractions with Like Denominators

Let us subtract the fractions 2/5 and 1/5 using rectangular models. We will represent 2/5

in this model by shading 2 out of 5 parts. We will further shade out 1 part from our shaded parts of the model to represent removing 1/5.

Subtracting Fractions with Like Denominators

We are now left with 1 part in the shaded parts of the model. Thus, we subtract the fractions in the following way:
2/5 - 1/5 = 1/5

Adding and Subtracting Fractions with Unlike Denominators

Adding Fractions with Unlike Denominators

When the denominators are different, the fractions are called unlike fractions. Let us add the fractions 1/5 and 1/3 using a rectangular model. We will represent the fraction 1/5 by dividing the model into 5 parts and shading 1 part and similarly the fraction 1/3 is represented by dividing the above model into 3 rows and shading 1 complete row.

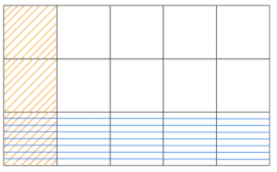Adding Fractions with unlike Denominators

We can see that our model is divided into 15 parts. This is our denominator. Note that there are 5 parts shaded blue and 3 parts shaded red (including the cell which is shaded both in red and blue). 

Therefore, 5 + 3 = 8  is the numerator. 

1/5 + 1/3 = 8/15
The denominator of 1/5 + 1/3 is 15 which is nothing but the Least Common Multiple (LCM) of  3 and 5. Now, let us add the same fractions by another method. We need to convert the given fractions to like fractions by taking the LCM of the denominators.
LCM (3, 5) = 15
An equivalent fraction of 1/5 with denominator 15 is:

1/5 × 3/3 = 3/15

Similarly, an equivalent fraction of 1/3 with denominator 1/5 is:
1/3 × 5/5 = 5/15
Now, that we have converted the given fractions to like fractions we can add the numerators and retain the same denominator.

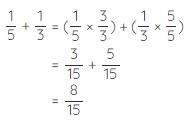
Subtracting Fractions with Unlike Denominators

To subtract unlike fractions, we follow the same steps as we did for the addition of unlike fractions:

• Take the LCM of the denominators.
• Convert the given fractions to equivalent fractions with the denominator as the LCM.
• Subtract the numerators.

Let us understand how to subtract unlike fractions using the area model.
3/5 - 1/3
This indicates that we have to remove 1/3rd part from 3/5. The fraction 3/5 can be shown using three hroizontal lines shaded among 5 lines shown. Similarly, the fraction 1/3 which is represented vertically will have 1 column shaded out of 3 columns. We can represent the difference of both the fractions using the following image.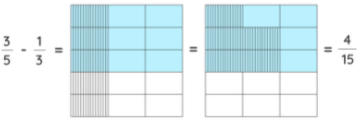
Subtracting Fractions with Different Denominators

We see that our model is divided into 15 parts. This is our denominator, or, in other words, the LCM of the denominators of the given fraction. As we need to remove 13  from 35, we will move the selected two parts which are not part of the 35, to remove it from 35.
We see that there are only 4 parts of the remaining which are not shaded out.
Therefore, 3/5 - 1/3 = 4/15

Adding and Subtracting Fractions with Whole Numbers

An easy way to add a whole number and fraction is to write it in mixed form. 

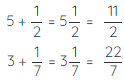
To subtract a fraction from a whole number, consider the following example.
3−1/2
Convert the whole number to its fractional form.
3 = 3/1
Subtract them like unlike fractions 3/1−1/2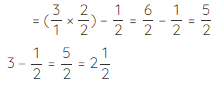

Important Notes

• Fractions with the same denominator are added using the formula:
  
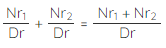
• The steps used to add fractions with different denominators are:
  a) Convert the given fractions to like fractions by taking the LCM of the denominator.  b) Find the equivalent fractions of the given fractions whose denominator is the LCM.  c) Add the numerators and retain the same denominator.

Tips

• For unlike fractions, never add or subtract the numerators and denominators directly.
  
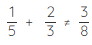
• When adding or subtracting unlike fractions, it is not necessary to find the LCM of the denominators. Any common multiple will do. So, simply multiplying the two denominators gives us a common multiple. This may lead to larger looking numbers, but it can be reduced to its lowest form.

Solved Examples

Example 1: Find the sum of 1/7 and 3/7.
Solution: The given fractions are like fractions. Add the numerators and retain the same denominator.

Example 2: Subtract 2/5 from 2/3.
Solution: The given fractions are unlike fractions. We have to find the LCM of the denominators and convert 2/5 and 2/3 to equivalent fractions of same denominator and then subtract.
LCM of  (3, 5) = 15

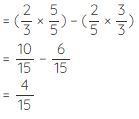
∴ The difference is 4/15.

Example 3: Add 3+1/3
Solution: To add the whole number and fraction, we use the following steps.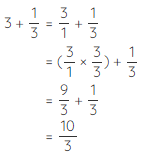


Example 4: How much pie would be left if Luke could eat only two-fifth of one whole pie
Solution: This situation is mathematically written as: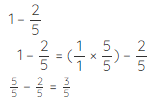

∴ 3/5th pie would be left.