NCERT Exemplar Solutions: Algebra | Mathematics for Class 6 PDF Download
Exercise Page: 107
In questions 1 to 23, out of the four given options, only one is correct. Write the correct answer.
Q1: If each match box contains 50 matchsticks, the number of matchsticks required to fill n such boxes is
(a) 50 + n
(b) 50n
(c) 50 ÷ n
(d) 50 – n
 View Answer
View Answer 
Ans: (b)
From the question it is given that, number of match sticks in each match box = 50
Then, the number of matchsticks required to fill n such boxes = 50 × n
= 50n
Q2: Amulya is x years of age now. 5 years ago her age was
(a) (5 – x) years
(b) (5 + x) years
(c) (x – 5) years
(d) (5 ÷ x) years
 View Answer
View Answer 
Ans: (c)
Current age of Amulya = x years
Then, 5 years ago her age was = (x – 5) years
Q3: Which of the following represents 6 × x
(a) 6x
(b) x/6
(c) 6 + x
(d) 6 – x
 View Answer
View Answer 
Ans: (a)
Here, 6 × x is equivalent to 6x.
So, option (A) is correct.
Q4: Which of the following is an equation?
(a) x + 1
(b) x – 1
(c) x – 1 = 0
(d) x + 1 > 0
 View Answer
View Answer 
Ans: (c)
An expression with a variable, constants and the sign of equality (=) is called an equation.
Q5: If x takes the value 2, then the value of x + 10 is
(a) 20
(b) 12
(c) 5
(d) 8
 View Answer
View Answer 
Ans: (b)
From the question it is given that, value of x is 2.
Now substitute the value of x in x + 10
= 2 + 10
= 12
Q6: If the perimeter of a regular hexagon is x metres, then the length of each of its sides is
(a) (x + 6) metres
(b) (x ÷ 6) metres
(c) (x – 6) metres
(d) (6 ÷ x) metres
 View Answer
View Answer 
Ans: (b)
We know that, perimeter of hexagon = number of sides × length of each side
Given, the perimeter of a regular hexagon is x metres
Then, the length of each of its side = (x/6) metres
= (x ÷ 6) metres
Q7: Which of the following equations has x = 2 as a solution?
(a) x + 2 = 5
(b) x – 2 = 0
(c) 2x + 1 = 0
(d) x + 3 = 6
 View Answer
View Answer 
Ans: (b)
Transforming – 2 from left hand side to right hand side it becomes 2.
Then, x = 2
Q8: For any two integers x and y, which of the following suggests that operation of addition is commutative ?
(a) x + y = y + x
(b) x + y > x
(c) x – y = y – x
(d) x × y = y × x
 View Answer
View Answer 
Ans: (a)
Let us assume a and b are the two integers,
Then, commutative law of addition = a + b = b + a
Where, a = x, b = y
Therefore, commutative law of addition = x + y = y + x
Q9: Which of the following equations does not have a solution in integers?
(a) x + 1 = 1
(b) x – 1 = 3
(c) 2x + 1 = 6
(d) 1 – x = 5
 View Answer
View Answer 
Ans: (c)
Consider the equation, 2x + 1 = 6
Transforming 1 from left hand side to right hand side it becomes -1.
2x = 6 – 1
2x = 5
X = 5/2
Q10: In algebra, a × b means ab, but in arithmetic 3 × 5 is
(a) 35
(b) 53
(c) 15
(d) 8
 View Answer
View Answer 
Ans: (c)
In arithmetic 3 × 5 is given by 15.
So, option (C) is correct.
Q11: In algebra, letters may stand for
(a) Known quantities
(b) Unknown quantities
(c) Fixed numbers
(d) None of these
 View Answer
View Answer 
Ans: (b)
In algebra, when a quantity is not known it is represented by using a letter.
So, option (B) is correct.
Q12: “Variable” means that it
(a) Can take different values
(b) Has a fixed value
(c) Can take only 2 values
(d) Can take only three values
 View Answer
View Answer 
Ans: (a)
The word ‘variable’ means something that can vary, i.e., change. The value of a variable is not fixed. We use a variable to represent a number and denote it by any letter such as l, m, n, p, x, y, z etc.
Q13: 10 – x means
(a) 10 is subtracted x times
(b) x is subtracted 10 times
(c) x is subtracted from 10
(d) 10 is subtracted from x
 View Answer
View Answer 
Ans: (c)
10 – x means that x is subtracted from the number 10.
So, correct option is (C).
Q14: Savitri has a sum of Rs x. She spent Rs 1000 on grocery, Rs 500 on clothes and Rs 400 on education, and received Rs 200 as a gift. How much money (in Rs) is left with her?
(a) x – 1700
(b) x – 1900
(c) x + 200
(d) x – 2100
 View Answer
View Answer 
Ans: (a)
From the question it is given that,
Savitri has a sum of Rs x
She spent money on grocery = ₹ 1000
She spent money on clothes = ₹ 500
She spent money on education = ₹ 400
She received gift = ₹ 200
Total money spent by Savitri = 1000 + 500 + 400 = ₹ 1900
Then,
Total money left with her after deducting = ₹ (x – 1900)
Therefore, money left with her after adding gift money = (x – 1900) + 200
= x – 1700
Q15: The perimeter of the triangle shown in Fig. 7.1 is
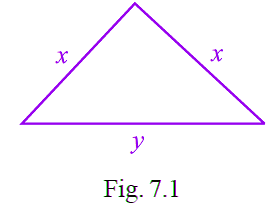
(a) 2x + y
(b) x + 2y
(c) x + y
(d) 2x – y
 View Answer
View Answer 
Ans: (a)
Given triangle is an isosceles triangle,
So, perimeter of an isosceles triangle = 2 × x + y
= 2x + y
Q16: The area of a square having each side x is
(a) x * x
(b) 4x
(c) x + x
(d) 4 + x
 View Answer
View Answer 
Ans: (a)
We know that, area of square = side * side
Given, square having a side x.
So, area of a square = x * x
= x2
Q17: The expression obtained when x is multiplied by 2 and then subtracted from 3 is
(a) 2x – 3
(b) 2x + 3
(c) 3 – 2x
(d) 3x – 2
 View Answer
View Answer 
Ans: (c)
From the question it is given that,
X is multiplied by 2 = x × 2 = 2x
Then, x is multiplied by 2 and then subtracted from 3 = 3 – 2x
Q18: q/2 = 3 has a solution
(a) 6
(b) 8
(c) 3
(d) 2
 View Answer
View Answer 
Ans: (a)
Consider the given equation q/2 = 3
By cross multiplication we get, q = 6
Q19: x – 4 = – 2 has a solution
(a) 6
(b) 2
(c) – 6
(d) – 2
 View Answer
View Answer 
Ans: (b)
Consider the given equation x – 4 = -2
Transform – 4 from left hand side to right hand side it becomes 4.
x = – 2 + 4
x = 2
Q20: 4/2 = 2 denotes a
(a) numerical equation
(b) algebraic expression
(c) equation with a variable
(d) false statement
 View Answer
View Answer 
Ans: (a)
4/2 = 2
By cross multiplication we get,
4 = 4
Q21: Kanta has p pencils in her box. She puts q more pencils in the box. The total number of pencils with her are
(a) p + q
(b) pq
(c) p – q
(d) p/q
 View Answer
View Answer 
Ans: (a)
From the question it is given that,
Kanta has p pencils in her box
She puts q more pencils in the box
The total number of pencils with her are = p + q
Q22: The equation 4x = 16 is satisfied by the following value of x
(a) 4
(b) 2
(c) 12
(d) –12
 View Answer
View Answer 
Ans: (a)
Consider the given equation 4x = 16
Then, value of x is,
x = 16/4 … [divide both numerator and denominator by 4]
x = 4
Q23: I think of a number and on adding 13 to it, I get 27. The equation for this is
(a) x – 27 = 13
(b) x – 13 = 27
(c) x + 27 = 13
(d) x + 13 = 27
 View Answer
View Answer 
Ans: (d)
Let us assume the number be ‘x’,
Then, adding 13 to the number = x + 13
Therefore, x + 13 = 27
In question 24 to 40, fill in the blanks to make the statements true:
Q24: The distance (in km) travelled in h hours at a constant speed of 40km per hour is __________.
 View Answer
View Answer 
The distance (in km) travelled in h hours at a constant speed of 40km per hour is 40h.
From the question,
Time taken to travel a distance = h hours
Travel at a speed of 40 km/h
So, total distance travelled = 40 × h
= 40h
Q25: p kg of potatoes are bought for Rs. 70. Cost of 1kg of potatoes (in Rs.) is __________.
 View Answer
View Answer 
p kg of potatoes are bought for Rs. 70. Cost of 1kg of potatoes (in Rs.) is 70/p.
Given, p kg of potatoes are bought for Rs. 70
Then, cost of 1 kg of potato = 70/p
Q26: An auto rickshaw charges Rs. 10 for the first kilometre then Rs. 8 for each such subsequent kilometre. The total charge (in Rs.) for d kilometres is __________.
 View Answer
View Answer 
An auto rickshaw charges Rs 10 for the first kilometre then Rs. 8 for each such subsequent kilometre. The total charge (in Rs.) for d kilometres is 2 + 8d.
From the question it is given that,
An auto rickshaw charges Rs. 10 for the first kilometre
Then Rs. 8 for each such subsequent kilometre.
So, the total charge (in Rs) for d kilometres is = 10 + (d – 1)8
= 10 + 8d – 8
= 2 + 8d
Q27: If 7x + 4 = 25, then the value of x is __________.
 View Answer
View Answer 
If 7x + 4 = 25, then the value of x is 3.
Consider the equation, 7x + 4 = 25
Transposing 4 from left hand side to right hand side it becomes -4,
7x = 25 – 4
7x = 21
x = 21/7
x = 3
Q28: The solution of the equation 3x + 7 = –20 is __________.
 View Answer
View Answer 
The solution of the equation 3x + 7 = –20 is -9.
Consider the equation, 3x + 7 = –20
Transposing 7 from left hand side to right hand side it becomes -7,
3x = – 20 – 7
3x = – 27
x = -27/3
x = – 9
Q29: ‘x exceeds y by 7’ can be expressed as __________.
 View Answer
View Answer 
‘x exceeds y by 7’ can be expressed as x – y = 7.
Q30: ‘8 more than three times the number x’ can be written as __________.
 View Answer
View Answer 
‘8 more than three times the number x’ can be written as 3x + 8.
As per the condition given in the question, three times the number x = 3x
So, 8 more than three times the number x = 3x + 8
Q31: Number of pencils bought for Rs x at the rate of Rs 2 per pencil is __________.
 View Answer
View Answer 
Number of pencils bought for Rs x at the rate of Rs 2 per pencil is x/2.
From the question it is given that, cost of pencil = ₹ x
No. of pencils bought for ₹ 2 = 1
Therefore, number of pencil bought for ₹ x = ₹ x/2
Q32: The number of days in w weeks is __________.
 View Answer
View Answer 
The number of days in w weeks is 7w.
We know that, there are 7 days in a week.
Therefore, number of days in w weeks is 7w.
Q33: Annual salary at r rupees per month along with a festival bonus of Rs. 2000 is __________.
 View Answer
View Answer 
Annual salary at r rupees per month along with a festival bonus of Rs. 2000 is 12r + 2000.
From the question it is given that,
Salary per month is r rupees
A festival bonus of ₹ 2000
Therefore, Annual salary at r rupees per month along with a festival bonus of Rs 2000 is ₹ 12r + 2000
Q34: The two digit number whose ten’s digit is ‘t’ and units’s digit is ‘u’ is __________.
 View Answer
View Answer 
The two digit number whose ten’s digit is ‘t’ and units’s digit is ‘u’ is 10t + u.
From the question,
Two digit number whose ten’s digit is ‘t’
Two digit number whose unit’s digit is ‘u’
Then, the number = 10 × t + 1 × u
= 10t + u
Q35: The variable used in the equation 2p + 8 = 18 is __________.
 View Answer
View Answer 
The variable used in the equation 2p + 8 = 18 is p.
The word ‘variable’ means something that can vary, i.e., change. The value of a variable is not fixed. We use a variable to represent a number and denote it by any letter such as l, m, n, p, x, y, z etc
Q36: x metres = __________ centimetres
 View Answer
View Answer 
x metres = x × 100 centimetres
We know that, 1 metre = 100 centimetre.
Therefore, x metres × 100 centimetres = 100x centimetres
Q37: p litres = __________ millilitres
 View Answer
View Answer 
p litres = p× 1000 millilitres
we know that, 1 litre = 1000 millilitres
Therefore, p litres × 1000 millilitres = 1000p milliliters.
Q38. r rupees = __________ paise
 View Answer
View Answer 
r rupees = 100r paise
We know that, 1 rupee = 100 paise
Therefore, r rupees = 100r paise
Q39: If the present age of Ramandeep is n years, then her age after 7 years will be __________.
 View Answer
View Answer 
If the present age of Ramandeep is n years, then her age after 7 years will be n + 7 years.
Q40: If I spend f rupees from 100 rupees, the money left with me is __________ rupees.
 View Answer
View Answer 
If I spend f rupees from 100 rupees, the money left with me is 100 – f rupees.
In question 41 to 45, state whether the statements are true or false.
Q41: 0 is a solution of the equation x + 1 = 0
 View Answer
View Answer 
False.
Consider the equation, x + 1 = 0
Then, x = -1
Q42: The equations x + 1 = 0 and 2x + 2 = 0 have the same solution.
 View Answer
View Answer 
True.
Consider equations x + 1 = 0
So, x = -1
Consider the equation, 2x + 2 = 0
Divide both the side by 2,
Then we get, x + 1 = 0
Therefore, x = – 1
Q43: If m is a whole number, then 2m denotes a multiple of 2.
 View Answer
View Answer 
Yes, If m is a whole number, then 2m denotes a multiple of 2.
So, given statement is True.
Q44: The additive inverse of an integer x is 2x.
 View Answer
View Answer 
False.
Additive inverse of x is – x
Q45: If x is a negative integer, – x is a positive integer.
 View Answer
View Answer 
Yes, If x is a negative integer, – x represents a positive integer.
So, given statement is True.
Q46: 2x – 5 > 11 is an equation.
 View Answer
View Answer 
False.
An expression with a variable, constants and the sign of equality (=) is called an equation.
Q47. In an equation, the LHS is equal to the RHS.
 View Answer
View Answer 
True
Q48. In the equation 7k – 7 = 7, the variable is 7.
 View Answer
View Answer 
False.
In the equation 7k – 7 = 7, the variable is k.
Q49: a = 3 is a solution of the equation 2a – 1 = 5
 View Answer
View Answer 
Yes, a = 3 is a solution of the equation 2a – 1 = 5.
So, given statement is True.
Q50: The distance between New Delhi and Bhopal is not a variable.
 View Answer
View Answer 
True
Distance between New Delhi and Bhopal is fixed.
Clearly, it is not a variable, so the statement is true.
Q51. t minutes are equal to 60t seconds.
 View Answer
View Answer 
True
Since 1 minute = 60 seconds
t minutes = 60t seconds
So, given statement is True.
Q52: x = 5 is the solution of the equation 3x + 2 = 20
 View Answer
View Answer 
False
We have, 3x + 2 = 20
⇒ 3x + 2 – 2 = 20 – 2
[Subtracting 2 from both sides]
⇒ 3x = 18
⇒ x= 18/3 = 6
x = 6, which is the solution of the given equation.
Q53: ‘One third of a number added to itself gives 8’, can be expressed as x/3 + 8 = x
 View Answer
View Answer 
False
Let the number be x.
One third of the number = x/3
According to the given question,
(x/3) + x = 8
Q54: The difference between the ages of two sisters Leela and Yamini is a variable.
 View Answer
View Answer 
False
Difference between the ages of two sisters Leela and Yamini is not a variable because Leela’s and Yamini’s ages are fixed. But the value of a variable is not fixed.
So, the statement false.
Q55: The number of lines that can be drawn through a point is a variable.
 View Answer
View Answer 
No, number of lines that can be drawn through a point is not a variable.
So, given statement is False.
In questions 56 to 74, choose a letter x, y, z, p etc...., wherever necessary, for the unknown (variable) and write the corresponding expressions:
Q56: One more than twice the number.
 View Answer
View Answer 
Let the number be x and twice the number x = 2x
Now, according to question,
The expression = 2x + 1
Hence, required expression is 2x + 1.
Q57: 20°C less than the present temperature.
 View Answer
View Answer 
Let the present temperature be f° C.
∴ Required expression
= Present temperature – 20°C = (f – 20)°C
Q58: The successor of an integer.
 View Answer
View Answer 
Let the integer be n.
Successor of n = n + 1
∴ Required expression = n + 1
Note: If 7 is added to a number, we get its successor.
Q59: The perimeter of an equilateral triangle, if side of the triangle is m.
 View Answer
View Answer 
Given, side of triangle is m.
In equilateral triangle, all sides are equal.
∴ Perimeter of an equilateral triangle =Sum of all the sides
= m + m + m = 3m
Hence, the perimeter of an equilateral triangle is 3m.
Q60: Area of the rectangle with length k units and breadth n units.
 View Answer
View Answer 
Given, length of rectangle = k units
Breadth of rectangle = n units
Now, area of rectangle = Length x Breadth = k x n = kn units
Hence, area of the rectangle is kn sq units.
Q61: Omar helps his mother 1 hour more than his sister does.
 View Answer
View Answer 
Let sister’s helping hours = x years
Then, Omar’s helping hour = Sister’s helping hour +1 = (x + 1)years
∴ Required expression = (x + 1) years
Q62: Two consecutive odd integers.
 View Answer
View Answer 
Let one odd integer be x.
So another consecutive odd integer will be x + 2.
Thus, Two consecutive odd integers are x, x + 2.
Q63: Two consecutive even integers.
 View Answer
View Answer 
Any even integer can be written as 2n, where n is an integer. So, next even integer will be 2n + 2.
Hence, two consecutive even integers are 2n and 2n + 2.
Q64:Multiple of 5.
 View Answer
View Answer 
Q65: The denominator of a fraction is 1 more than its numerator.
 View Answer
View Answer 
∴ The denominator of the fraction can be expressed as x + 1.
∴ The fraction = x/(x + 1).
Q66: The height of Mount Everest is 20 times the height of Empire State building.
 View Answer
View Answer 
∴ Height of Mount Everest = 20y.
Q67: If a note book costs Rs. p and a pencil costs Rs. 3, what is the total cost (in Rs.) of two note books and one pencil?
 View Answer
View Answer 
Cost of a pencil = Rs. 3
∴ Cost of two notebooks and one pencil = Rs. (2p + 3).
Q68: z is multiplied by -3 and the result is subtracted from 13.
 View Answer
View Answer 
– 3z subtracted from 13 = 13 – (-3z) = 13 + 3z.
Q69: p is divided by 11 and the result is added to 10.
 View Answer
View Answer 
If p is divided by 11, it is given as = P/11.
Now when P/11 is added to 10, it gives = (P/11)+10
Q70:x times of 3 is added to the smallest natural number.
 View Answer
View Answer 
x times of 3 = 3x
And smallest natural number = 1.
So, 3x added to 1 = 3x + 1.
Q71: 6 times q is subtracted from the smallest two-digit number.
 View Answer
View Answer 
6 times q = 6q.
The smallest two-digit number = 10.
6q subtracted from 10 = 10 – 6q.
Q72: Write two equations for which 2 is the solution.
 View Answer
View Answer 
The required equations are 3y + 4 = 10 and 2x – 3 = 1.
In both equations, 2 is the solution.
Q73: Write an equation for which 0 is a solution.
 View Answer
View Answer 
The required equation is 2t + 3 = 3, which has the solution t = 0.
Q74: Write an equation whose solution is not a whole number.
 View Answer
View Answer 
The required equation is x + 1 = 0.
Its solution is x = -1, which is not a whole number.
Q75: A pencil costs Rs. p and a pen costs Rs. 5p.
 View Answer
View Answer 
A pen costs 5 times the cost of a pencil.
Q76: Leela contributed Rs. y towards the Prime Minister’s Relief Fund. Leela is now left with Rs.(y + 10000).
 View Answer
View Answer 
Amount left with Leela is Rs. 10,000 more than the amount she contributed towards the Prime Minister’s Relief Fund.
Q77: Kartik is n years old. His father is 7n years old.
 View Answer
View Answer 
The age of Kartik’s father is seven times the age of Kartik.
Q78: The maximum temperature on a day in Delhi was p°C. The minimum temperature was (p – 10)°C.
 View Answer
View Answer 
The minimum temperature on a day in Delhi was 10°C less than the maximum temperature.
Q79: John planted t plants last year. His friend Jay planted 2t + 10 plants that year.
 View Answer
View Answer 
Last year, Jay planted 10 more plants than twice the plants planted by his friend John.
Q80: Sharad used to take p cups of tea a day. After having some health problems, he takes p – 5 cups of tea a day.
 View Answer
View Answer 
Sharad reduced his tea consumption per day by 5 cups after having some health problems.
Q81: The number of students dropping out of school last year was m. The number of students dropping out of school this year is m – 30.
 View Answer
View Answer 
The number of students dropping out this year is 30 less than the number of students who dropped out last year.
Q82: The price of petrol was Rs. p per litre last month. The price of petrol now is Rs. (p – 5) per litre.
 View Answer
View Answer 
The price of petrol per litre decreased by Rs. 5 this month compared to last month.
Q83: Khader’s monthly salary was Rs. P in the year 2005. His salary in 2006 was Rs. (P + 1000).
 View Answer
View Answer 
Khader’s monthly salary increased by Rs. 1000 in the year 2006 compared to 2005.
Q84: The number of girls enrolled in a school last year was q. The number of girls enrolled this year in the school is 3g – 10.
 View Answer
View Answer 
The number of girls enrolled this year is 10 less than 3 times the number of girls enrolled last year.
Q85: Translate each of the following statements into an equation, using x as the variable:
(a) 13 subtracted from twice a number gives 3.
(b) One fifth of a number is 5 less than that number.
(c) Two-third of number is 12.
(d) 9 added to twice a number gives 13.
(e) 1 subtracted from one-third of a number gives 1.
 View Answer
View Answer 
(a) 13 subtracted from twice a number gives 3.
Let the number be x. Twice the number = 2x.
According to the question: 2x – 13 = 3.
(b) Let the number be x.
One-fifth of a number is x=x/5
5 less than that number x = x-5
One-fifth of the number = x/5.
According to the question: x/5 = x – 5.
(c) Let the number be x.
Two-thirds of a number is 12.
Two-thirds of the number x= 2x/3.
According to the question: 2x/3 = 12.
(d) Let the number be x.
Twice the number = 2x.
Now, 9 is added to 2x = 9 + 2x
According to question, 9 + 2x = 13.
(e) Let the number be x.
One-third of the number x= x/3.
Now, 1 is subtracted from x/3 = x/3 - 1
According to the question: x/3 – 1 = 1.
Q86: Translate each of the following statements into an equation:
(a) The perimeter (p) of an equilateral triangle is three times its side (a).
(b) The diameter (d) of a circle is twice its radius (r).
(c) The selling price (s) of an item is equal to the sum of the cost price (c) of the item and the profit (p) earned.
(d) Amount (a) is equal to the sum of principal (p) and interest (i).
 View Answer
View Answer 
(a) We have given,
Perimeter of an equilateral triangle = 3 (the side of an equilateral triangle)
⇒ p = 3a
(b) We have given,
Diameter of a circle
= 2 (the radius of the circle)
⇒ d = 2r
(c) We have given,
Selling price = cost price + profit
⇒ s = c + p
(d) We have given,
Amount = principal + interest
⇒ a = p + i
Q87: Let Kanika’s present age be x years. Complete the following table, showing ages of her relatives: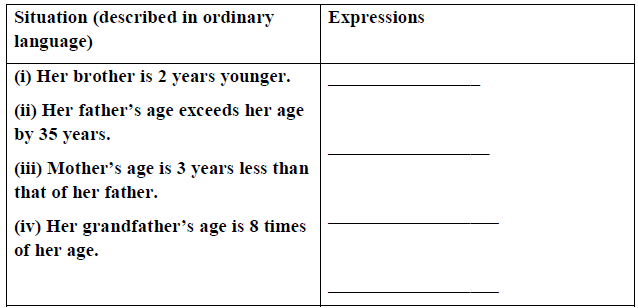
 View Answer
View Answer 
Completed table is as follows:
Q88: If m is a whole number less than 5, complete the table and by inspection of the table, find the solution of the equation 2m – 5 = – 1:
 View Answer
View Answer 
If m is a whole number less than 5, the completed table is as follows: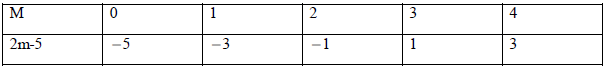
Now as it can be seen in the table that as m = 2,
2m-5 = -1.
So solution of 2m-5 =-1 is
m = 2.
Q89: A class with p students has planned a picnic. Rs. 50 per student is collected, out of which Rs. 1800 is paid in advance for transport. How much money is left with them to spend on other items?
 View Answer
View Answer 
No. of students in a class = p
Per student fee collected = Rs 50
Money paid in advance = Rs 1800
Money left = Rs (50p – 1800)
Q90: In a village, there are 8 water tanks to collect rainwater. On a particular day, x litres of rainwater is collected per tank. If 100 litres of water was already there in one of the tanks, what is the total amount of water in the tanks on that day?
 View Answer
View Answer 
No. of tanks = 8
Water collected per tank = x litres
Amount of water in one tank = 100 litres
Total water in all tanks = (8x + 100) litres
Q91: What is the area of a square whose side is m cm?
 View Answer
View Answer 
Side of the square = m cm
Area of the square = m × m sq. cm
Q92: Perimeter of a triangle is found by using the formula P = a + b + c, where a, b, and c are the sides of the triangle. Write the rule that is expressed by this formula in words.
 View Answer
View Answer 
Rule: P = a + b + c where a, b and c are the sides of the triangle in words is expressed as,
Sum of all sides of a triangle is equal to its perimeter.
Q93: Perimeter of a rectangle is found by using the formula P = 2 (l + w), where l and w are the length and breadth of the rectangle, respectively. Write the rule that is expressed by this formula in words.
 View Answer
View Answer 
Rule: The perimeter of a rectangle is twice the sum of its length and breadth.
Q94: On my last birthday, I weighed 40 kg. If I put on m kg of weight after a year, what is my present weight?
 View Answer
View Answer 
Last year’s weight = 40 kg
Weight gain after a year = m kg
Present weight = (40 + m) kg
Q95: Length and breadth of a bulletin board are r cm and t cm, respectively.
(i) Length of the aluminium strip required to frame the board, if 10 cm extra strip is required = (2(r + t) + 10) cm.
(ii) If x nails are used to repair one board, nails required for 15 boards = 15x.
(iii) Area of the cloth required to cover one board = (r × t) + 500 sq. cm.
Total cloth area required for 8 boards = 8((r × t) + 500) sq. cm.
(iv) Expenditure for making 23 boards, if carpenter charges Rs x per board = 23x.
 View Answer
View Answer 
We have given, length of the board = r cm and breadth = t cm.
(i) The length of aluminium strip to frame the board = Perimeter of the board
= 2(length + breadth)
= 2(r + t) cm
But 10 cm extra strip is required to fix it properly.
∴ Total length of the aluminium strip = 2(r + t) cm + 10 cm.
(ii) Number of nails required to repair 1 board = x.
∴ Number of nails required to repair 15 boards = 15 × x = 15x.
(iii) Area of the cloth required for 1 board = Area of the board
= length × breadth
= r cm × t cm
= (rt) sq cm
Area of the cloth required for 8 boards
= 8 × (rt) sq cm
= 8rt sq cm
But 500 sq cm extra cloth per board is required to cover the edges.
∴ For 8 boards we need 8 × 500 sq cm
= 4000 sq cm extra cloth.
Thus, the total area of the cloth required
= (8rt + 4000) sq cm
(iv) The carpenter charges for 1 board = Rs. x.
∴ The carpenter charges for 23 boards
= Rs. (23 × x) = Rs. 23x
Q96: Sunita is half the age of her mother Geeta. Find their ages
(i) After 4 years?
(ii) Before 3 years?
 View Answer
View Answer 
Let the present age of Sunita be x years.
The present age of her mother Geeta = 2(Sunita’s present age) = 2x years.
(i) After 4 years,
Sunita’s age = (x + 4) years
Geeta’s age = (2x + 4) years
Before 3 years,
Sunita’s age = (x – 3) years
Geeta’s age = (2x – 3) years.
Q97: Match the items of Column I with that of Column II:

 View Answer
View Answer 
(i) ➝ (B), (ii) ➝ (E), (iii) ➝ (C), (iv) ➝ (C), (v) ➝(A)
(i) The number of corners of a quadrilateral is 4, i.e., a constant.
(ii) The variable in the equation 2p + 3 = 5 is p.
(iii) We have given, x + 2 = 3
⇒ x + 2 – 2 = 3 – 2
[Subtracting 2 from both sides]
⇒ x = 1, which is the solution of the given equation.
(iv) We have given, 2p + 3 = 5
⇒ 2p + 3- 3 = 5- 3
[Subtracting 3 from both sides]
⇒ 2p = 2
⇒ 2p/2 = 2/2
⇒ p = 1, which is the solution of the given equation.
(v) Equality sign (=) is used in an equation.
|
48 videos|331 docs|23 tests
|
FAQs on NCERT Exemplar Solutions: Algebra - Mathematics for Class 6
| 1. What is the importance of Algebra in NCERT Exemplar solutions? |  |
| 2. How can I effectively use NCERT Exemplar Solutions for Algebra? |  |
| 3. Are NCERT Exemplar Solutions sufficient for preparing for Algebra exams? |  |
| 4. What types of Algebra problems can I expect in the NCERT Exemplar Solutions? |  |
| 5. How do NCERT Exemplar Solutions help in improving problem-solving skills in Algebra? |  |

















