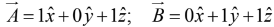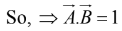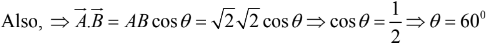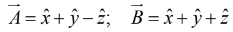Vector Algebra | Mathematical Methods - Physics PDF Download
Vector Operations
Vector quantities have both direction as well as magnitude such as velocity, acceleration,
force and momentum etc. We will use  for any general vector and its magnitude by
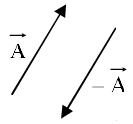
for any general vector and its magnitude by In diagrams vectors are denoted by arrows: the length of the arrow is proportional to the magnitude of the vector, and the arrowhead indicates its direction. Minus
In diagrams vectors are denoted by arrows: the length of the arrow is proportional to the magnitude of the vector, and the arrowhead indicates its direction. Minus (-
(-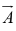 )is a vector with the same magnitude as
)is a vector with the same magnitude as 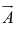 but of opposite direction.
but of opposite direction.
We define four-vector operations: addition and three kinds of multiplication.
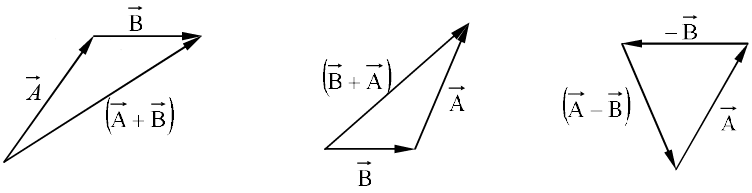
- Addition of two vectors
Place the tail of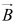 at the head of
at the head of 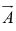 ; the sum,
; the sum,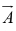 +
+ is the vector from the tail of
is the vector from the tail of 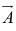 to the head of
to the head of 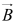
Addition is commutative: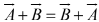
Addition is associative: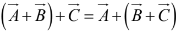
To subtract a vector, add its opposite: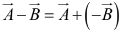
- Multiplication by scalar
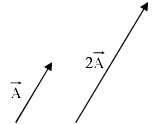
Multiplication of a vector by a positive scalar a, multiplies the magnitude but leaves the direction unchanged. (If a is negative, the direction is reversed.) Scalar multiplication is distributive: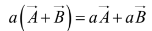
- Dot product of two vectors
The dot product of two vectors is define by
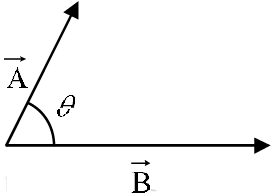
where θ is the angle they form when placed tail to tail. Note that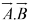 . is itself a scalar.
. is itself a scalar.
The dot product is commutative,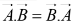
and distributive,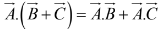
Geometrically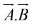 is the product of A times the projection of
is the product of A times the projection of 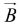 along
along 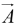 (or the product of B times the projection of
(or the product of B times the projection of 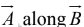 )
)
If the two vectors are parallel,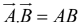
If two vectors are perpendicular, then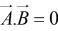
Law of cosines
Let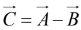 and then calculate dot product of
and then calculate dot product of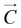 with itself.
with itself.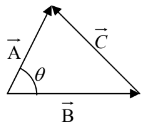

C2 A2 + B2 - 2AB cosθ - Cross product of two vectors
 The cross product of two vectors is define by
The cross product of two vectors is define by
where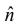 is a unit vector(vector of length 1) pointing perpendicular to the plane of
is a unit vector(vector of length 1) pointing perpendicular to the plane of 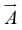 and
and 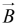 . Of course there are two directions perpendicular to any plane “in” and “out.”
. Of course there are two directions perpendicular to any plane “in” and “out.”
The ambiguity is resolved by the right-hand rule:
let your fingers point in the direction of first vector and curl around (via the smaller angle) toward the second; then your thumb indicates the direction of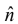 . (In figure
. (In figure 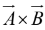 points into the page;
points into the page; 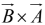 points out of the page)
points out of the page)
The cross product is distributive,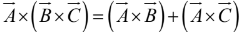
but not commutative.
In fact,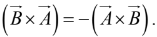
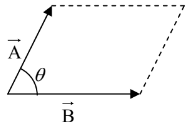
Geometrically, is the area of the parallelogram generated by
is the area of the parallelogram generated by 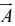 and
and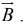
If two vectors are parallel, their cross product is zero.
In particular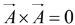 for any vector
for any vector 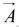
Vector Algebra: Component Form
Let  and
and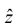 be unit vectors parallel to the x, y and z axis, respectively. An arbitrary
be unit vectors parallel to the x, y and z axis, respectively. An arbitrary
vector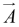 can be expanded in terms of these basis vectors
can be expanded in terms of these basis vectors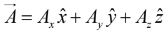
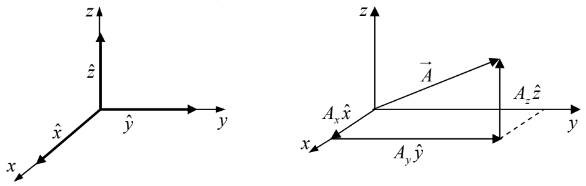
The numbers Ax , Ay , and Az are called component of 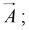 geometrically, they are the projections of
geometrically, they are the projections of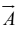 along the three coordinate axes.
along the three coordinate axes.
(i) Rule: To add vectors, add like components.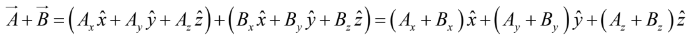
(ii) Rule: To multiply by a scalar, multiply each component.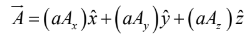
Because 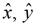 and
and 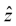 are mutually perpendicular unit vectors
are mutually perpendicular unit vectors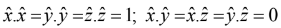
Accordingly, 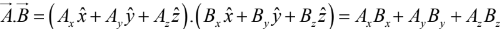
(iii) Rule: To calculate the dot product, multiply like components, and add.
In particular, 
Similarly, 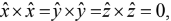
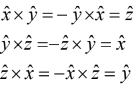
(iv) Rule: To calculate the cross product, form the determinant whose first row is  whose second row is
whose second row is  (in component form), and whose third row is
(in component form), and whose third row is
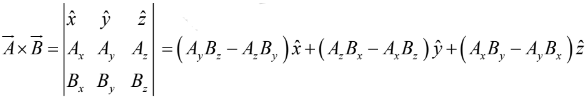
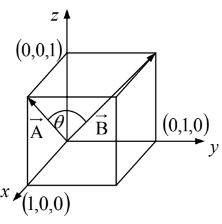
Example 1: Find the angle between the face diagonals of a cube.
The face diagonals
and
are
Example 2: Find the angle between the body diagonals of a cube.
The body diagonals
and
are
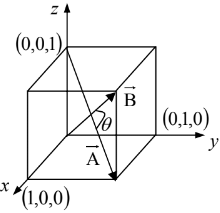
Example 3: Find the components of the unit vector nˆ perpendicular to the plane shown in the figure.
The vectors
and
can be defined as
Triple Products
Since the cross product of two vectors is itself a vector, it can be dotted or crossed with a
third vector to form a triple product.
(i) Scalar triple product: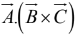
Geometrically  is the volume of the parallelepiped generated by
is the volume of the parallelepiped generated by 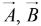 and
and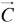 , since
, since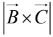 is the area of the base, and
is the area of the base, and 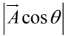 is the altitude. Evidently,
is the altitude. Evidently,
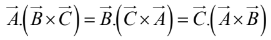
In component form 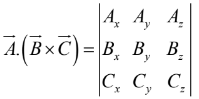
Note that the dot and cross can be interchanged: 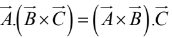
(ii) Vector triple product: 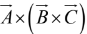
The vector triple product can be simplified by the so-called BAC-CAB rule: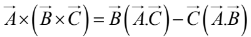
Position, Separation and Displacement Vectors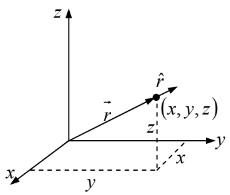
The location of a point in three dimensions can be described by listing its Cartesian
coordinates (x,y,z) . The vector to that point from the origin is called the position vector: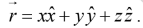
Its magnitude, 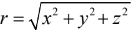 is the distance from the origin,
is the distance from the origin,
and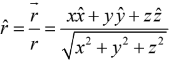 is a unit vector pointing radially outward.
is a unit vector pointing radially outward.
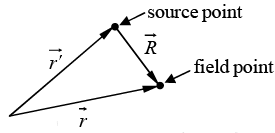
Note: In electrodynamics one frequently encounters problems involving two points-
typically, a source point, 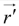 where an electric charge is located, and a field point,
where an electric charge is located, and a field point,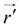 , at which we are calculating the electric or magnetic field. We can define separation vector
, at which we are calculating the electric or magnetic field. We can define separation vector
from the source point to the field point by 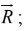
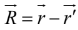
Its magnitude is 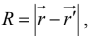
and a unit vector in the direction from 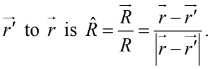
In Cartesian coordinates, 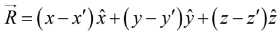
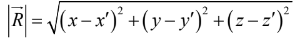
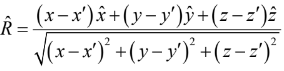
Infinitesimal Displacement Vector 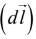
The infinitesimal displacement vector, from (x,y,z) to ( x + dx, y + dy, z + dz), is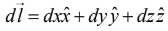
Area Element
For closed surface area element is perpendicular to the surface pointing outwards as shown in figure below.
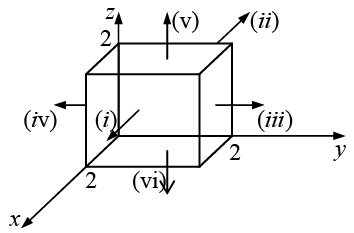
(i) For x = 2 plane,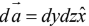
(ii) For x = 0 plane,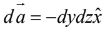
(iii) For y = 2 plane,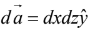
(iv) For y = 0 plane,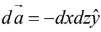
(v) For z = 2 plane,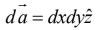
(vi) For z = 0 plane,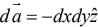
For open surface area element is shown in figure below (use right hand rule)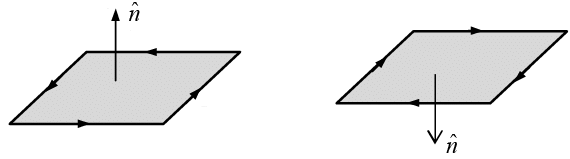
Volume Element
Volume element dτ = dxdydz
Curvilinear Coordinates
Spherical Polar Coordinates
In spherical polar coordinate any general point P lies on the surface of a sphere. The
spherical polar coordinates r,θ,∅ of a point P are defined in figure shown below; r is
the distance from the origin (the magnitude of the position vector), θ (the angle drawn
from the z axis) is called the polar angle, and ∅ (the angle around from the x axis) is the
azimuthal angle.
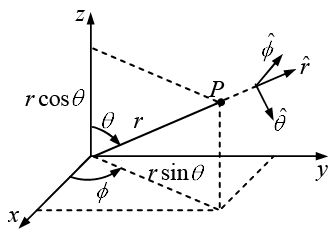
Their relation to Cartesian coordinates (x,y,z) can be read from the figure:
x = r sinθ cos∅,y = r sinθ sin∅, z = r cosθ
and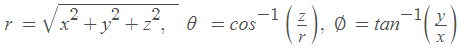
The range of r is 0 → ∞, θ goes from 0 → π , and ∅ goes from0 → 2π .
Figure shows three unit vectors , pointing in the direction of increase of the
, pointing in the direction of increase of the
corresponding coordinates. They constitute an orthogonal (mutually perpendicular) basis
set (just like ), and any vector
), and any vector 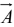 can be expressed in terms of them in the usual
can be expressed in terms of them in the usual
way:
Ar , Aθ , and A∅ are the radial, polar and azimuthal components of 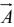 .
.
Infinitesimal Displacement Vector 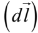
An infinitesimal displacement in the 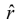 direction is simply dr (figure a), just as an
direction is simply dr (figure a), just as an
infinitesimal element of length in the x direction is dx :
dlr = dr
On the other hand, an infinitesimal element of length in the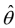 direction (figure b) is r dθ
direction (figure b) is r dθ
dlθ = rdθ
Similarly, an infinitesimal element of length in the 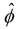 direction (figure c) is rsin θd∅
direction (figure c) is rsin θd∅
dl∅ = r sinθd∅
Thus, the general infinitesimal displacement dl is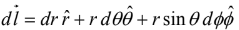
This plays the role (in line integrals, for example) that =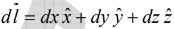 played in
played in
Cartesian coordinates.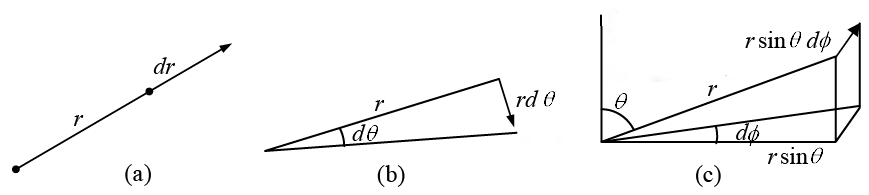
Area Element
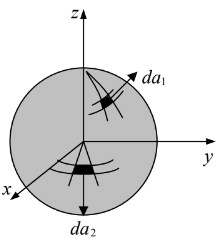
If we are integrating over the surface of a sphere, for instance,
then r is constant, whereas θ and ∅ change, so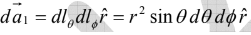
on the other hand, if the surface lies in the xy plane, then θ is
constant (θ = π/2) while r and ∅ vary, then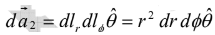
Volume Element(d/τ)
The infinitesimal volume element dτ, in spherical coordinates, is the product of the three infinitesimal displacements: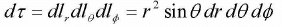
Transformation of Vector to Spherical Polar
We can transform any vector in Cartesian coordinates to Spherical polar coordinate as 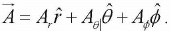
Thus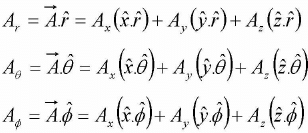
where x = rsin θcos∅, y = rsinθsin∅, z = r cosθ
and use table given below: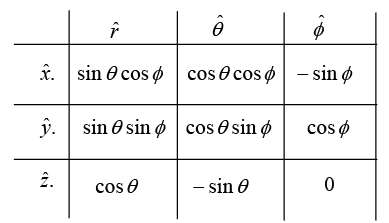
Cylindrical Polar Coordinates
The cylindrical coordinates r,∅,z o f a point P are defined in figure. Notice that ∅ has the same meaning as in spherical coordinates, and z is the same as Cartesian; r is the distance to P from the z axis, whereas the spherical coordinate /'is the distance from the origin. The relation to Cartesian coordinates is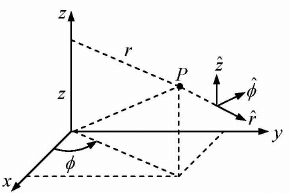
x = rcos∅, y = r sin∅, z = z
The range of r is 0 → ∞ , ∅ goes from 0 → 2π , and z from - ∞ to ∞
The infinitesimal displacements are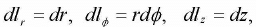
so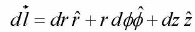
and volume element is dτ = r dr dФ, dz.
We can transform any vector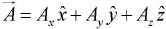 in Cartesian coordinates to cylindrical coordinates as
in Cartesian coordinates to cylindrical coordinates as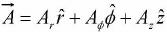
Thus,
|
78 videos|18 docs|24 tests
|
FAQs on Vector Algebra - Mathematical Methods - Physics
| 1. What is vector algebra? |  |
| 2. How is vector algebra used in IIT JAM? |  |
| 3. What are the basic operations in vector algebra? |  |
| 4. How do I find the magnitude of a vector using vector algebra? |  |
| 5. Can vector algebra be used in three-dimensional space? |  |