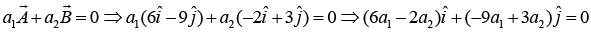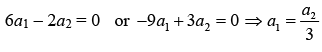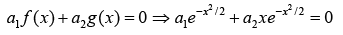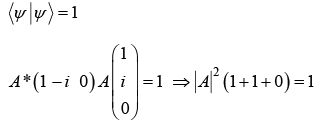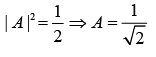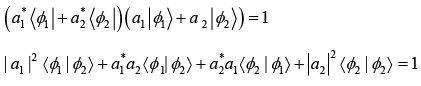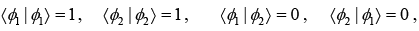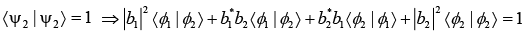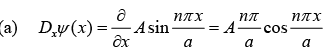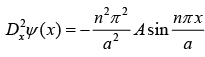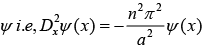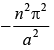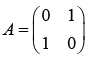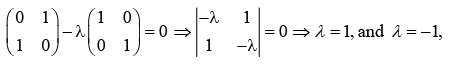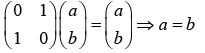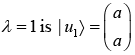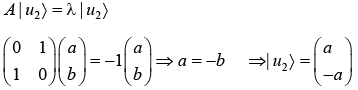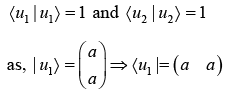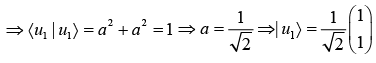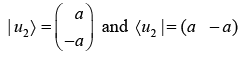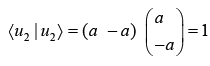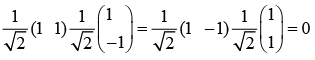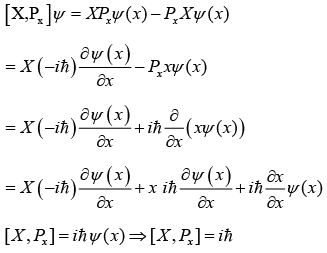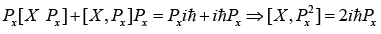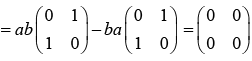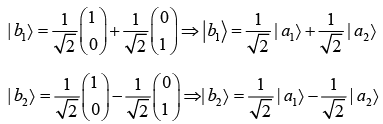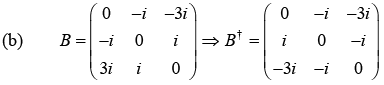Linear Vector Space | Modern Physics PDF Download
A set of vectors Ψ, ϕ, X, ... and set of scalars a, b, c defined over vector space which will follow a rule for vector addition and rule for scalar multiplication.
(i) Addition Rule
If Ψ and ϕ are vectors of elements of a space, their sum Ψ + ϕ is also vector of the same space.
- Law of Commutativity: Ψ + ϕ = ϕ + Ψ
- Law of Associativity: (Ψ + ϕ) + X = Ψ + (ϕ + X)
- Law of Existence of a null vector and inverse vector: Ψ + (-Ψ) = (-Ψ) + Ψ = 0
(ii) Multiplication rule
- The product of a scalar with a vector gives another vector. If Ψ and ϕ are two vectors of the space, any linear combination aΨ + bϕ is also a vector of the same space, where a and b being scalars.
- Distributive with respect to addition:
a(ϕ + Ψ) = aϕ + aΨ , (a + b)Ψ = aΨ + bΨ - Associativity with respect to multiplication of scalars: a (bΨ) = (ab)Ψ
- For each element Ψ, there must exist a unitary element I and a non-zero scalar O such that: I ·Ψ = Ψ·I = Ψ, O·Ψ = Ψ·O = O
Scalar Product
The scalar product of two functions ϕ(x) and Ψ(x) is given by (Ψ ϕ) = ∫Ψ*(x)ϕ(x)dx. where ϕ(x) and Ψ(x) are two com plex function of variable x , ϕ* (x) and Ψ* (x) are complex conjugate of ϕ(x) and Ψ(x) respectively.
The scalar product of two function ϕ (x, y, z) and Ψ(x, y, z) in 3-dimension is defined as (Ψ,ϕ) = ∫Ψ*ϕdxdydz
Hilbert Space
The Hilbert space H consists of a set of vectors Ψ, ϕ, X and set of scalar a,b,c which satisfies the following four properties:
(i) H is a linear space
(ii) H is a linear space that defines the scalar product which is strictly positive.
- (Ψ, ϕ) = (ϕ, Ψ)*
- (Ψ, aϕ1 + bϕ2) = a (Ψ, ϕ1) + b(Ψ, ϕ2)
- (Ψ, Ψ) = |Ψ|2 ≥ 0
(iii) H is separable i.e.,
- ║Ψ - Ψn║ ≤ 0
(iv) H is complete ║Ψ - Ψm║ = 0 , when m →∞, n →∞
Dimension and Basis of a Vectors.
Linear independency:
A set of N vectors ϕ1 ,ϕ2, ϕ3 ......ϕn, is said to be linearly independent if and only if the solution of the equation 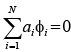 is a1 = a2 = a3 = a4 = 0.... an = 0 , otherwise ϕ1 ,ϕ2, ϕ3 ......ϕn is said to be linear dependent.
is a1 = a2 = a3 = a4 = 0.... an = 0 , otherwise ϕ1 ,ϕ2, ϕ3 ......ϕn is said to be linear dependent.
The dimension of a space vector is given by the maximum number of linearly independent vectors that a space can have.
The maximum number of linearly independent vectors of a space is N i.e., ϕ1 ,ϕ2, ϕ3 ......ϕN , this space is said to be N dimensional. In this case any vector Ψ of the vector space can be expressed as linear combination,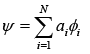
Orthonormal Basis
Two vectors ϕi ,ϕj is said to be orthonormal, if their scalar product (ϕi, ϕj) = δi, j, where δi, j is kronekar delta that means δi, j = 0 , when i ≠ j and δi, j = 1 , if i = j.
Square Integrable Function
If scalar product 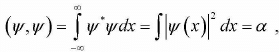 where α is a positive finite number, then Ψ (x) is said to be square integrable.
where α is a positive finite number, then Ψ (x) is said to be square integrable.
The square intergable function can be treated as probability distribution function, if α = 1 and Ψ is said to be normalized.
Dirac Notation
Dirac introduced what was to become an invaluable notation in quantum mechanics, state vector Ψ which is square integrable function to what he called a ket vector |Ψ〉 and its conjugate Ψ by a bra 〈Ψ| and scalar product (ϕ, Ψ) bra-ket 〈ϕ|Ψ〉 (In summary Ψ → |Ψ〉, Ψ* → 〈Ψ| and (ϕ, Ψ) = 〈ϕ|Ψ〉), where 〈ϕ, Ψ〉 = ∫ϕ*(r, t)Ψ(r, t)d3r.
Properties of kets, bras and bra-kets.
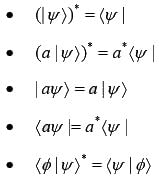
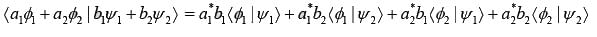
- |Ψ〉 is normalized, if 〈Ψ|Ψ〉 = 1
- Schwarz inequality
|〈Ψ| ϕ〉|2 ≤ 〈Ψ|Ψ〉 〈ϕ|ϕ〉, which is analogically derived from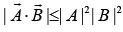
- Triangular inequality,
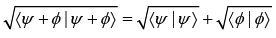
- Orthogonal states, 〈Ψ| ϕ〉 = 0
- Orthonormal state, 〈Ψ| ϕ〉 = 0, 〈Ψ| Ψ〉 = 1, 〈ϕ|ϕ〉 = 1
- Forbidden quantities: If |Ψ〉 and |ϕ〉 belong to same vector space, then product of the type |Ψ〉|ϕ〉 and 〈ϕ|〈Ψ| are forbidden. They are nonsensical.
- If |Ψ〉 and |ϕ〉 however belong to two different vector space, then |ϕ〉 ⊗|Ψ〉 represent tensor product of |Ψ〉 and |ϕ〉
Operator
An operator A is the mathematical rule that when applied to a ket |ϕ〉 will transform it into another ket |Ψ〉 of the same space and when it acts on any bra 〈X| , it transforms it into another bra 〈ϕ| , that means A|ϕ〉 = |Ψ〉 and 〈X| A = 〈ϕ|
Example of Operator-
Identity operator, I | Ψ〉 = |Ψ〉
Pairity operator, π|Ψ(r)〉 = |Ψ(-r)〉
Gradiant operator, ∇ Ψ (r) and Linear momentum operator,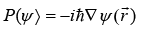
 |
Origin Of Quantum Mechanics MCQ Level – 1
|
Start Test |
Linear Operator
A is linear operator if,
- A(λ1 | Ψ1〉 + λ2 | Ψ2〉) = λ1 A| Ψ1〉 + λ2A|Ψ2〉
- Product of two linear operator A and B is written as AB , which is defined as, (AB) | Ψ〉 = A(B|Ψ〉)
Matrix Representation of Operator
If |Ψ〉 is in orthonormal basis of |ui〉 is defined as
|Ψ〉 c1|u1〉 + c2 |u2〉 + ... |Ψ〉 = Σci|ui〉 , where ci =〈ui|Ψ〉
Then, the ket |Ψ〉 is defined as 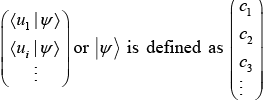 vector.
vector.
- The corresponding bra 〈Ψ| is defined as (〈u1|Ψ〉*〈u2 |Ψ〉*...) or (c*1,c*2 ...c*j), which is a row matrix.
- Operator A is represented as Matrix A whose Matrix element Aij is defined as 〈ui|A|uj〉 in basis of |ui〉.
- Transpose of operator A is represented as Matrix AT, whose matrix element is defined as ATij = 〈uj |A| ui〉
- Hermitian adjoint of Matrix A is represented as A†, whose matrix element is defined as A† = 〈uj |A| ui〉
Hermitian conjugate A† of a matrix A can be found in two steps:
Step I: Find transpose of A i.e., convert row into column i.e., AT
Step II: Then take complex conjugate of each element of AT.
Properties of Hermitian Adjoint A†
- (A†)† = A
- (λA)† = λ*A†
- (A + B)† = A† + B†
- (AB)† = B† A†
Eigen Value of Operator
If an operator A is defined as, A |ψ〉 = λ|ψ〉, then
λ is said to be eigen value and |ψ〉 is said to be eigenvector corresponding to operator.
Correspondence between Ket and Bra
If A |ϕ〉 = |ψ〉, then 〈ϕ|A† 〈ψ| , where A† is Hermitian adjoint of matrix or operator A.
Hermitian Operator
An operator A is said to be Hermitian if,
A† = A i.e., Matrix element 〈ui| A|uj〉 = (〈uj |A|ui〉)*
- The eigen values of Hermitian matrix is real
- The eigen vectors corresponding to different eigen values are orthogonal.
Commutator
If A and B are two operators, then the commentator [A, B] is defined as AB - BA.
If [A,B] = 0 , then it is said that operators A and B commute to each other.
Properties of commutator:
- Antisymmetry: [A, B] = -[B, A]
- Linearity: [A, B + C + D] = [A, B] + [A, C] + [A, D]
- Distributive: [AB, C] + [A, C] B + A[B, C]
- Jacobi Identity: [A, [B, C]] + [B,[C, A]] + C[A, B]] = 0
 |
Download the notes
Linear Vector Space
|
Download as PDF |
Set of Commuting Observables
- If two operators A and B commute and if |ψ〉 is eigen vector of A , then B |ψ〉 is also an eigen vector of A , with the same eigenvalue.
- If two operators A and B commute and if |ψ1〉 and |ψ2〉 are two eigenvectors of A with different eigenvalues, then Matrix element 〈ψ1 | B | ψ2〉 is zero.
- If two operators A and B commute, then one can construct an orthonormal basis of state with eigenvectors common to A and B.
Projection Operator
- The operator P is said to be projection operator, if P† = P and P2 = P
- The product of two commutating projection operators P1 and P2 is also a projection operator.
- The sum of two projection operators is generally not a projection operator.
- The sum of projection operator, P1 + P2 + P3 + .... is projection operator, if Pi ,Pj are mutually orthogonal.
Example 1: Prove that f(x) = x, g (x) = x2 , h(x) = x3 are linearly independent.
For linear independency 12 3
a1f(x) + a2g(x) + a3h(x) = 0 ⇒ a1x + a2x2 + a3x3 = 0
Equating the coefficient of x, x2 and x3 on both sides, one can get.
a1 = 0, a2 = 0, a3 = 0, so f(x), g(x) and h(x) are linearly independent.
Example 2: Prove that vector 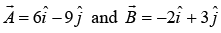 are linearly dependent.
are linearly dependent.
So,are linearly dependent.
Example 3: 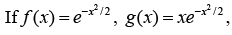 then prove that f (x) and g (x) are orthogonal as well as linearly independent.
then prove that f (x) and g (x) are orthogonal as well as linearly independent.
For linear independency:
So, f (x) and g (x) are linearly independent.
For orthogonality: (f(x)g (x)) = ∫f*(x)g(x)dxScalar product of f (x) and g (x) is zero i.e., orthogonal.
Example 4: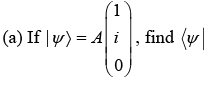
(b) Find the value of A such that |ψ〉 is normalized.
(b) For normalization condition-
Example 5: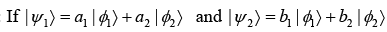
It is given that 〈ϕi | ϕj〉 = δij then,
(a) Find the condition for |ψ1〉 and |ψ2〉 to be normalized.
(b) Find the condition for |ψ1〉 and |ψ2〉 to be orthogonal.
(a) If |ψ1〉 is normalized, then |ψ1 | ψ1〉 = 1
It is given that
So, |a1|2 + |a2|2 = 1
Similarly, for |ψ2〉 to be normalized-
⇒ |b1|2 + |b2|2 = 1
(b) For |ψ1〉 and |ψ2〉 to be orthogonal,
⇒ a*1b*1 + a*2b2 = 0
Similarly, from 〈ψ2 | ψ1〉 = 0 ⇒ b*1a1 + b*2a2 = 0
Example 6: If S operator is defined as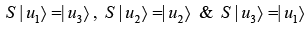
and 〈ui | uj〉 = δij ; i,j = 1, 2, 3
(a) Construct S matrix
(b) Prove that S is hermitian matrix
The Matrix
where matrix element Sij = 〈ui |S| uj〉
∵ S = S† i.e., S matrix is Hermitian.
Example 7: If Dx is defined as ∂/∂x and ψ(x) = A sin nπx/a
(a) Operate Dx on ψ (x)
(b) Operate D2x on ψ(x)
(c) Which one of the above gives eigen value problem?
(c) When D2x operate on
So, operation of D2x(x) on ψ(x) =A sin nπx/a give eigen value problem with eigen value
Example 8: If operator A is given by, 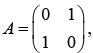 then
then
(a) find eigen value and eigen vector of A.
(b) normalized the eigen vector.
(c) prove both eigen vector are orthogonal.
(a)
for eigen value
| A - λI | = 0
The eigen vector corresponding to λ = 1,
A |u1〉 = λ|u1〉
so, eigen vector corresponding to
eigen vector corresponds to λ = -1
(b) For normalised eigen vector.
Similarly,
(c) for orthogonality, 〈u1 | u2〉 = 〈u2 | u1〉 = 0
Example 9: If momentum operator Px is defined as 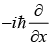 and position operator X is defined as XΨ(x) = xΨ(x)
and position operator X is defined as XΨ(x) = xΨ(x)
(a) Find the value of commutator [X, Px]
(b) Find the value of [X2 , Px]
(c) Find the value of [X , P2x]
(a): [X, Px] (X Px - PxX)
Operate on both side ψ
(b) [X2, Px] = [X·X, Px] = X [X, Px]+ [X, Px]X = Xiℏ + iℏX= 2iℏX
(c) [X, P2x] = [X,Px ·Px]
Example 10: (a) Prove that PΨ = |Ψ〉〈Ψ| is projection operator
(b) Operate PΨ on |ϕ〉
(c) Operate PΨ on 〈ϕ|
(d) Operate PΨ on |Ψ〉 and 〈Ψ|
(e) Find the eigen value of any projection operator.
(a)
So, PΨ is projection operator.
⇒ PΨ = 0, PΨ = I, so eigen value of PΨ = 0 or 1
Example 11: 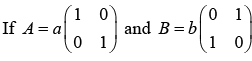
(a) Find the value of [A, B]
(b) Write down eigen vector of B in the basis of eigen vector of A.
(a): [A, B] = AB - BA
{As [A, B] = 0 , so A and B will commute}
(b) Eigen vector of A isfor eigen value λ1 = a
for eigen value λ2 = a
Eigen vector of B isfor eigen value λ1 = b
for eigen value λ2∂ = -b
Example 12: 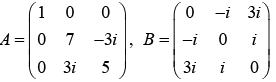
(a) find A†
(b) find B†
(c) which one of A and B have real eigen value?
(a)
A† = A , so A is Hermitian.
i.e., B† = -B
So, it is not Hermitian rather it is Anti-Hermitian.
(c) The eigen value of A matrix is real because A is Hermitian.
|
37 videos|16 docs|19 tests
|
FAQs on Linear Vector Space - Modern Physics
| 1. What is Dirac notation and how is it used in linear vector spaces? |  |
| 2. What is the significance of Dirac notation in the context of IIT JAM exam? |  |
| 3. Can you provide an example of how Dirac notation is used to represent vectors and operators in quantum mechanics? |  |
| 4. What are the advantages of using Dirac notation in quantum mechanics? |  |
| 5. Are there any limitations or drawbacks to using Dirac notation in quantum mechanics? |  |