Damped Oscillator | Oscillations, Waves & Optics - Physics PDF Download
Damped Harmonic Oscillation
The majority of the oscillatory systems in everyday life suffer some sort of irreversible energy loss due to frictional or viscous heat generation while they are oscillating. Their
amplitude of oscillation dies away with time. Such oscillation is called damped harmonic
oscillation.
Consider the mass-spring system, body of mass m attached to spring with spring
constant k is released from position x0 (measured from equilibrium position) with
velocity v ; the mass is subject to a frictional damping force which opposes its motion,
and is directly proportional to its instantaneous velocity Fres = −bv
The quantity v is a positive constant, whose value depends on the properties of the
material providing the resistance. The minus sign indicates that the force resists the
motion, so it is directed opposite to the velocity.
The total force on the body is the sum of the restoring force F = −kx , and the resistive
force
Fres: Fnet = F + Fres = −kx − bv
Using Newton second law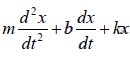 = 0 ⇒
= 0 ⇒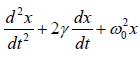 = 0
= 0
Here, we define the constant γ such that, 2γ = b/m called damping constant and
ω0 = √k /m is the natural frequency of undamped oscillator.
Assuming a solution of the form x(t) = Ceαt
On differentiation, we get 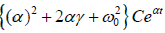 = 0
= 0
The solution (forω ) from the quadratic formula is: α = 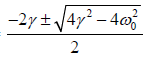
⇒ α = 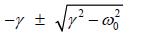
Thus the solution is x(t) = 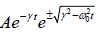 =
= 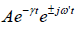 where ω ' =
where ω ' = 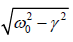
If we consider the quantity under the square root sign, we see that there are three
possibilities.
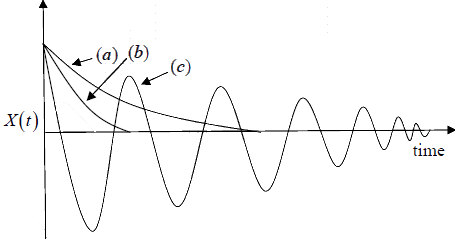
Case 1: Overdamped Case: If the damping coefficient is large, then γ >ω0 and ω′
will be imaginary. Hence x (t )will be a negative exponential function. It is shown in
figure (a).
Case 2: Critically Damped Case: If ω0 =γ , then the square root vanishes. In this case,
the solution is again a negative exponential function which goes to zero quicker than the
overdamped case, as shown in figure (b).
Case 3: Underdamped Case: If ω0 >γ then the quantity under the square root is
positive and we have a real number for ω ′ . The solution for ‘ x ’ is then
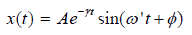
This is the solution of the damped harmonic oscillator. The oscillatory motion is shown
in figure (c).
Time Period: of the damped harmonic oscillator is: T' = 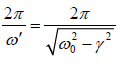
This shows that due to damping the time period slightly increased.
Logarithmic Decrement: This measure the rate at which the amplitude decay
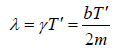
Mean Life time(τm) : It is the time taken for the amplitude to decay to 1/e of the initial
value. When t = 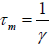 , Amplitude = A/e
, Amplitude = A/e 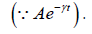
Energy of the Damped Oscillator
Kinetic energy (K)
The displacement of a damped harmonic oscillator is x (t ) = 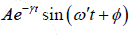
The instantaneous velocity is
u = 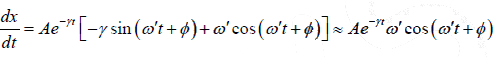
The approximation is done as γ <<ω0
Thus, kinetic energy is K = 1/2mu2 = 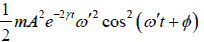
Potential energy (U)
U = 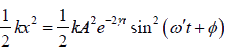
Total energy (E)
E = K + U = 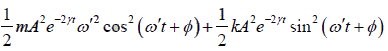
⇒E = 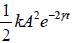 Since γ <<ω0 thus ω′ =
Since γ <<ω0 thus ω′ = 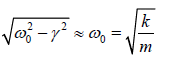
This shows that the energy of the oscillator decreases with time, the exponential decay of
energy is show below.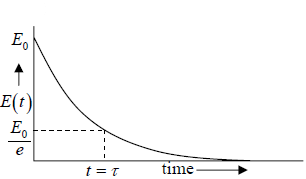
Power Dissipation: It is the rate at which the energy is lost
P = 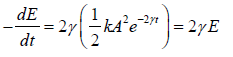
Relaxation Time: It is the time taken for the total energy to decay to 1/e of its initial value E0. If τ is the relaxation time, then at t =τ , we shall have E = 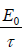 .
.
Thus 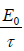 =
= 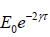 This gives relaxation time τ =
This gives relaxation time τ = 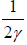
Thus we can also write power dissipated as P = E/τ
and energy can be expressed as E(t) = 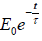 .
.
Quality Factor (Q): It is defined as the 2π times the ratio of the energy stored in the
system to the energy lost per period.
Q = 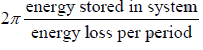
Energy stored in the system is E while the energy loss per period is PT , thus
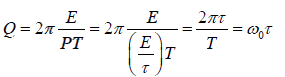
This shows that, lower the damping, higher the value of Q.
Now energy can be written in term of Q as E(t) = 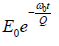
It means that Q is related to the number of oscillation over which the energy fall to 1/e of
its original value E0 , which is also called the relaxation time. This happens in time, t =τ ,
where τ is given by

In one period (T ) number of oscillation is =1
In time τ the number of oscillation = n , then n = 
Thus the energy falls to 1/e of its original value after n= Q/2π = cycle of free oscillation.
Relation between relaxation time, mean time and Quality factor:
Let N is the number of oscillation in time 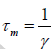
While n is the number of oscillation in time τ = 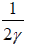
Thus, relation between mean and relaxation time is τm = 2t
In one period (T ) number of oscillation is =1
In time τm the number of oscillation = N
 or
or 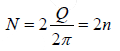
|
54 videos|22 docs|14 tests
|
FAQs on Damped Oscillator - Oscillations, Waves & Optics - Physics
| 1. What is damped harmonic oscillation? |  |
| 2. How is the energy of a damped oscillator affected? |  |
| 3. What is the significance of the quality factor in a damped oscillator? |  |
| 4. Can a damped oscillator exhibit oscillation without any external force? |  |
| 5. How is the behavior of a damped oscillator different from that of an undamped oscillator? |  |
















